链式二叉树

news2024/10/7 0:27:25

链式二叉树

  • 一，相关函数接口实现
    • 1，前序遍历
    • 2，中序遍历
    • 3，后序遍历
    • 4，节点个数
    • 5，叶子结点个数
    • 6，树的高度
    • 7，第K层结点个数
    • 8，查找值为X的结点
    • 9，通过前序遍历数组构建二叉树
    • 10，销毁二叉树
    • 11，层序遍历
    • 12，判断是否为完全二叉树
  • 二，OJ题实战
    • 1，单值二叉树
    • 2，检查两棵树是否相同
    • 3，另一棵树的子树
    • 4，二叉树的前序遍历
    • 5，二叉树的中序遍历
    • 6，二叉树的后序遍历
    • 7，对称二叉树
    • 8，二叉树的建立及遍历
    • 9，判断是否为平衡二叉树

一，相关函数接口实现

所谓链式二叉树，就是存储方式是链式存储的，所以首先要定义出二叉树结点的结构体：

typedef struct TreeNode
{
	int val;
	struct TreeNode* left;
	struct TreeNode* right;
}TreeNode;

为了方便测试后面的函数，在这里手动创建一个二叉树
在这里插入图片描述

TreeNode* BuyTreeNode(int x)
{
	TreeNode* node = (TreeNode*)malloc(sizeof(TreeNode));
	if (!node)
	{
		perror("malloc fail");
		exit(-1);
	}
	node->val = x;
	node->left = node->right = NULL;
	return node;
}
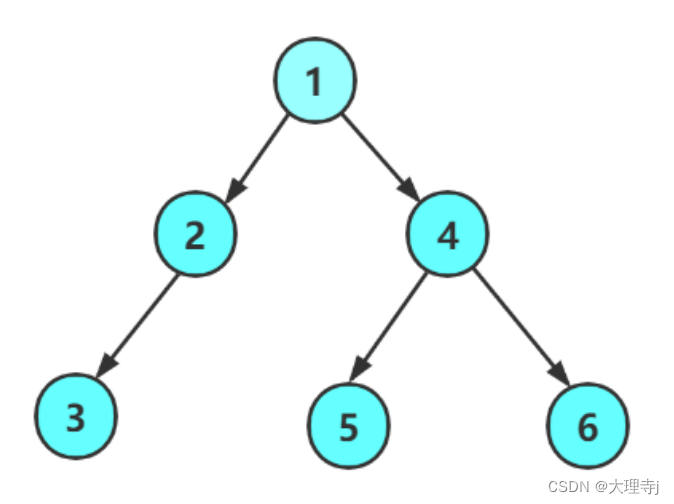
int main()
{
	TreeNode* n1 = BuyTreeNode(1);
	TreeNode* n2 = BuyTreeNode(2);
	TreeNode* n3 = BuyTreeNode(3);
	TreeNode* n4 = BuyTreeNode(4);
	TreeNode* n5 = BuyTreeNode(5);
	TreeNode* n6 = BuyTreeNode(6);
	n1->left = n2;
	n1->right = n4;
	n4->left = n5;
	n4->right = n6;
	n2->left = n3;
	return 0;
}

1，前序遍历

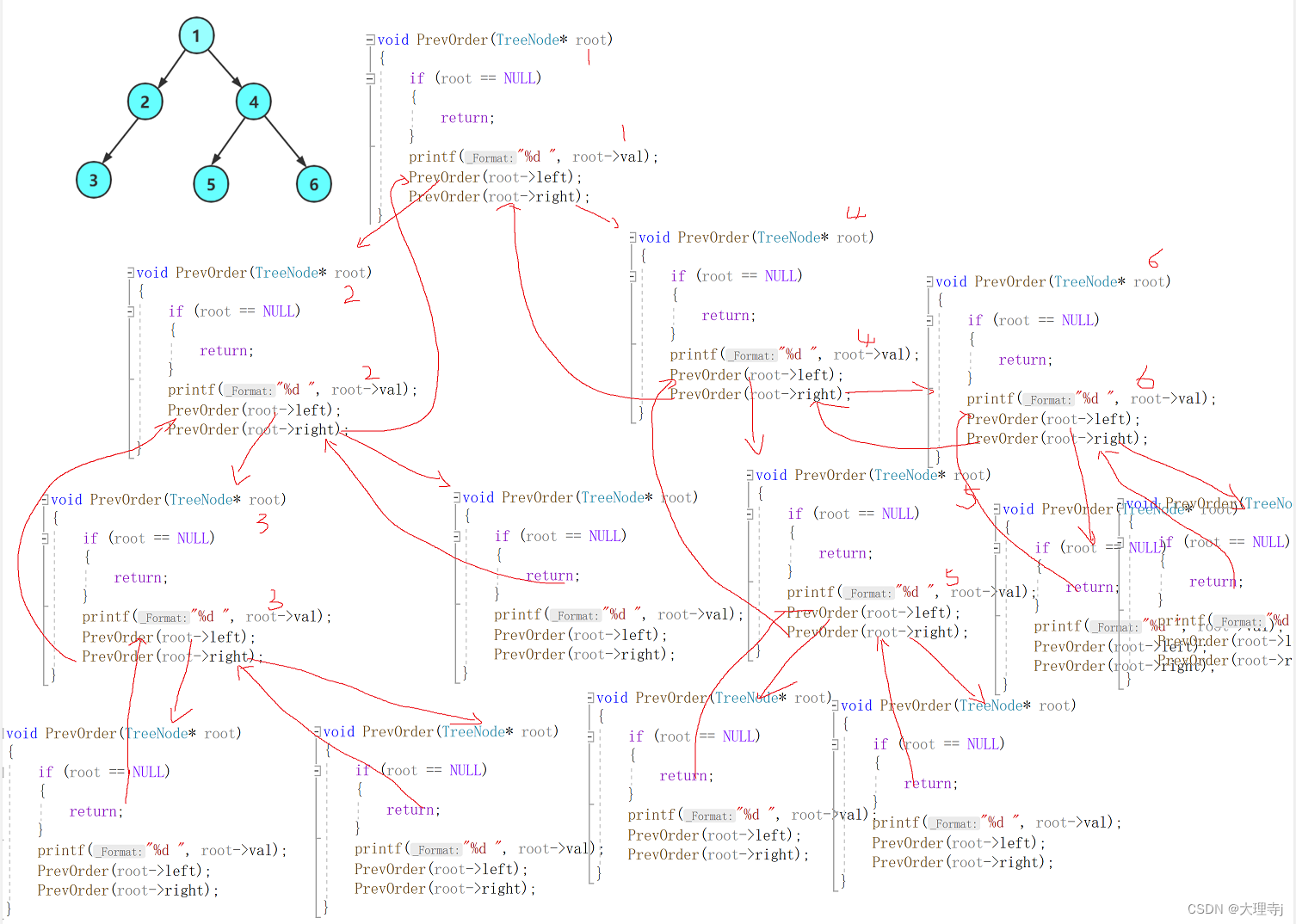
前序遍历就是先遍历的顺序为：根节点-左子树-右子树

void PrevOrder(TreeNode* root)
{
	if (root == NULL)
	{
		return;
	}
	printf("%d ", root->val);
	PrevOrder(root->left);
	PrevOrder(root->right);
}

二叉树这里的相关问题都会大量使用递归，为了更直观的看到是如何递归的可以画一下递归展开图：
在这里插入图片描述

2，中序遍历

中序后序与前序没有什么区别就是先遍历根节点与后遍历根节点的区别

void InOrder(TreeNode* root)
{
	if (root == NULL)
	{
		return;
	}
	InOrder(root->left);
	printf("%d ", root->val);
	InOrder(root->right);
}

3，后序遍历

void PostOrder(TreeNode* root)
{
	if (root == NULL)
	{
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d ", root->val);
}

4，节点个数

递归采用的是分治思想，不断地把问题进行细分，直到不可细分为止。
数结点个数可以这样看：
对于根节点来说，树的结点数就是根的左子树的节点数+根的右子树的节点数+1（这个1就是根节点）

int TreeSize(TreeNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	return TreeSize(root->left) + TreeSize(root->right) + 1;
}

5，叶子结点个数

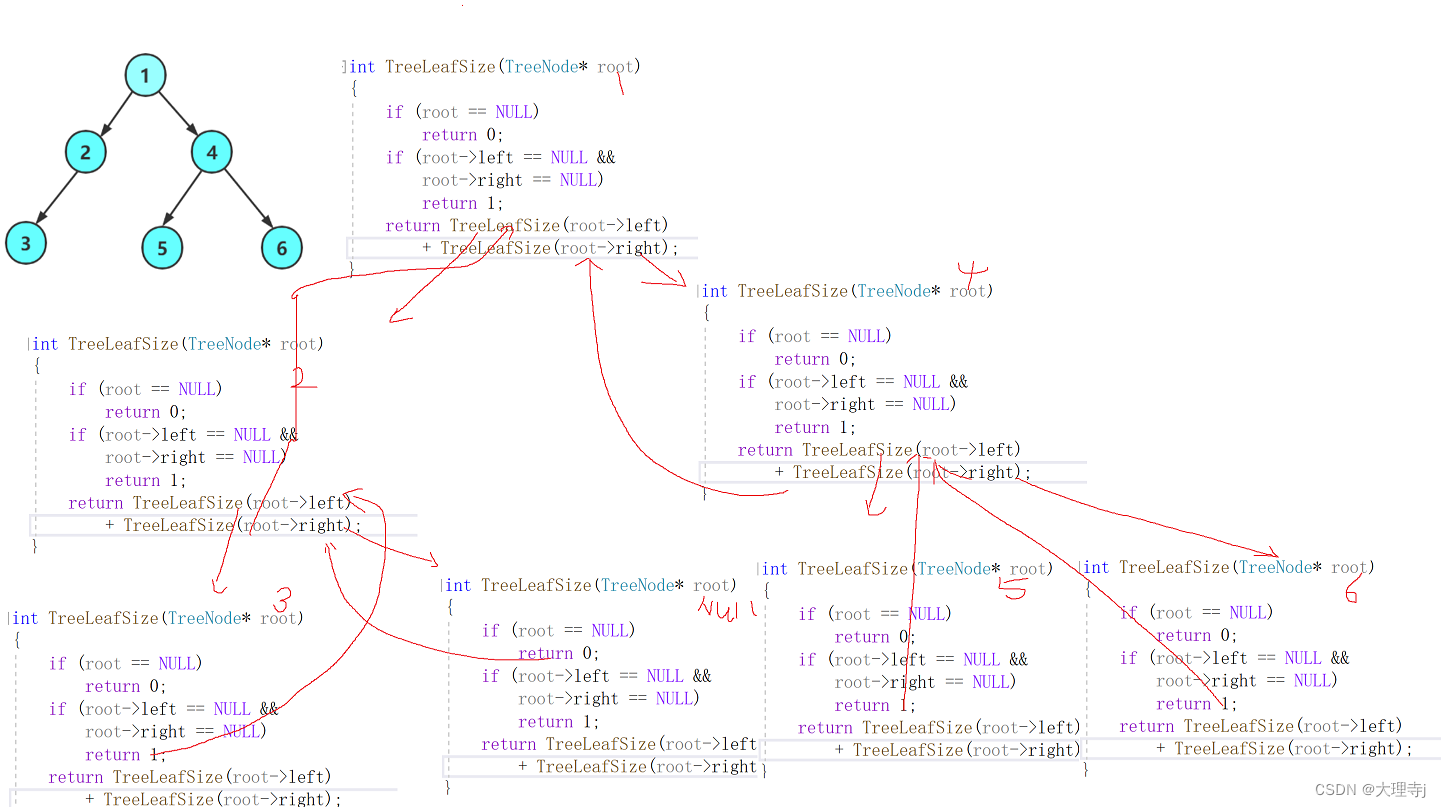
叶子结点个数与上面的节点个数有所不同，不能每次都加上根节点的‘1’，而是当某个根节点的左右子树都是空树的时候再返回1。

int TreeLeafSize(TreeNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}
	return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}

递归展开图：
在这里插入图片描述

6，树的高度

树的高度思想与树的节点数思想类似，但是有区别：
是左右子树高度大的那一个+根节点的‘1’

int TreeHeight(TreeNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	int leftheight = TreeHeight(root->left);
	int rightheight = TreeHeight(root->right);
	return leftheight > rightheight ?  leftheight + 1 : rightheight + 1;
}

7，第K层结点个数

第k层是相对于根节点的，那么就相当于左右子树的k-1层，这样分治下去直到k==1就返回1。

int TreeLevelSize(TreeNode* root,int k)
{
	if (root == NULL)
	{
		return 0;
	}
	if (k == 1)
	{
		return 1;
	}
	return TreeLevelSize(root->left, k - 1) + TreeLevelSize(root->right, k - 1);
}

8，查找值为X的结点

如果根节点的值就为x，那么直接返回。否则就先从左子树找，再找不到就去右子树找，直到找到为止，如果树中没有此结点就返回空。

TreeNode* TreeFind(TreeNode* root, int x)
{
	if (root == NULL)
	{
		return NULL;
	}
	if (root->val == x)
	{
		return root;
	}
	TreeNode* left = TreeFind(root->left, x);
	if (left)
	{
		return left;
	}
	TreeNode* right = TreeFind(root->right, x);
	if (right)
	{
		return right;
	}
	return NULL;
}

9，通过前序遍历数组构建二叉树

后面的一个OJ题：二叉树的建立及遍历与这个问题相同，放在后面讲解。

10，销毁二叉树

销毁二叉树也是采用递归的形式删除，但要注意的是应该先删除左右子树再删除根节点，因为如果先删除根节点就无法找到左右子树了。

void TreeDestory(TreeNode** root)
{
	if (*root == NULL)
	{
		return;
	}
	TreeDestory(&((*root)->left));
	TreeDestory(&((*root)->right));
	free(*root);
	*root = NULL;
}

11，层序遍历

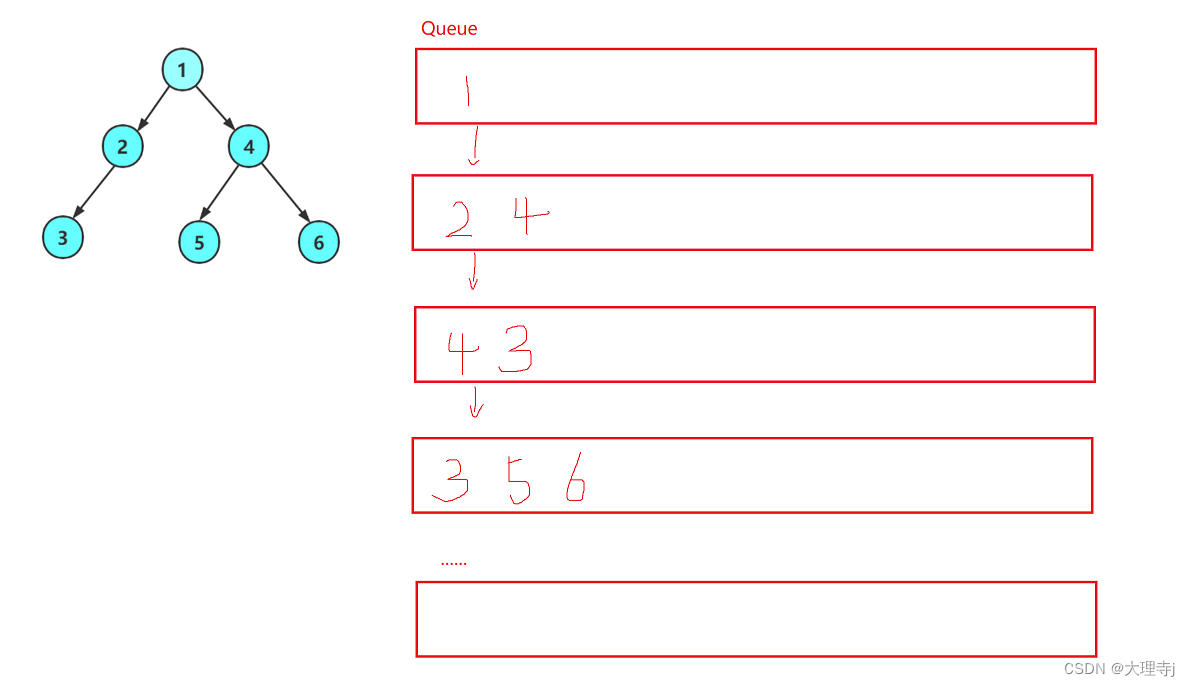
剩余的两个问题与前面有所不同，前面的问题都是采用递归的方式解决的，层序遍历和判断是否为完全二叉树都是通过借助队列迭代实现的。
首先将根节点进队列，在根节点出队列的时候把左右子树（当左右子树不是空树时）带入到队列中，依次进行，直到队列为空为止。
在这里插入图片描述

void LevelOrder(TreeNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root)
	{
		QueuePush(&q, root);
	}
	while (!QueueEmpty(&q))
	{
		TreeNode* front = QueueFront(&q);
		printf("%d ", front->val);
		QueuePop(&q);
		if (front->left)
		{
			QueuePush(&q, front->left);
		}
		if (front->right)
		{
			QueuePush(&q, front->right);
		}
	}
	QueueDestroy(&q);
}

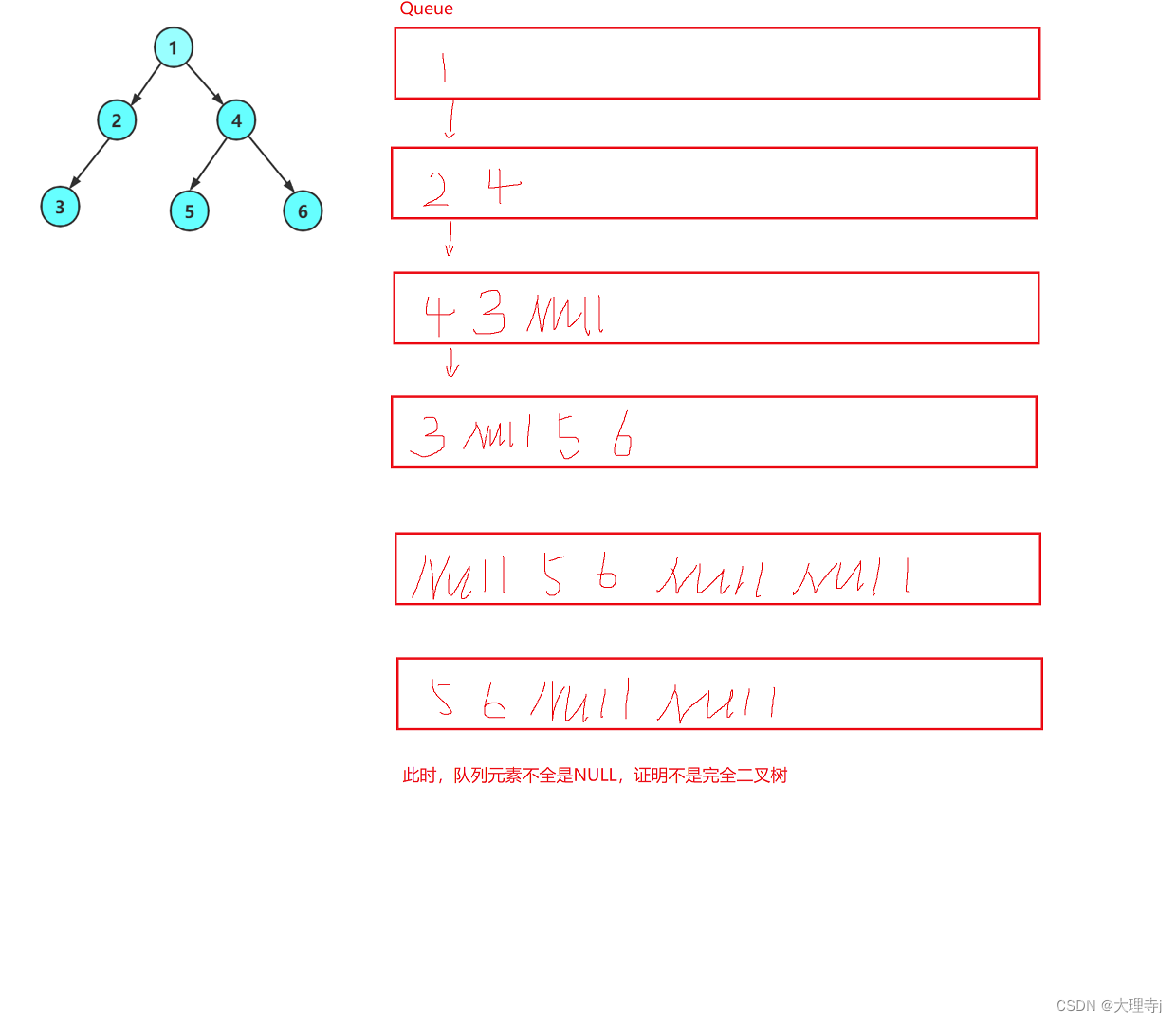
12，判断是否为完全二叉树

这个问题最好的解决方法就是利用层序遍历，不过与上面的层序遍历有些区别，就是左右子树为空树的时候也入队列，当出队列的元素是NULL时，若是完全二叉树，则此时队列中的元素都是NULL，反之不是完全二叉树。
在这里插入图片描述

bool TreeComplete(TreeNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root)
	{
		QueuePush(&q, root);
	}
	while (!QueueEmpty(&q))
	{
		TreeNode* front = QueueFront(&q);
		QueuePop(&q);
		if (front == NULL)
		{
			while (!QueueEmpty(&q))
			{
				TreeNode* tmp = QueueFront(&q);
				QueuePop(&q);
				if (tmp != NULL)
				{
					return false;
				}
			}
		}
		if (front)
		{
			QueuePush(&q, front->left);
			QueuePush(&q, front->right);
		}
	}
	QueueDestroy(&q);
	return true;
}

二，OJ题实战

1，单值二叉树

链接: 单值二叉树
在这里插入图片描述

同样采用分治的思想，先比较根与左右子树是否相等，如果不等直接返回false，如果相等，那么左右子树作为新的根节点进行递归。

bool isUnivalTree(struct TreeNode* root){
    if(root==NULL)
    {
        return true;
    }
    if(root->left&&root->val!=root->left->val)
    {
        return false;
    }
    if(root->right&&root->val!=root->right->val)
    {
        return false;
    }
    return isUnivalTree(root->left)&&isUnivalTree(root->right);
}

2，检查两棵树是否相同

链接: 检查两棵树是否相同
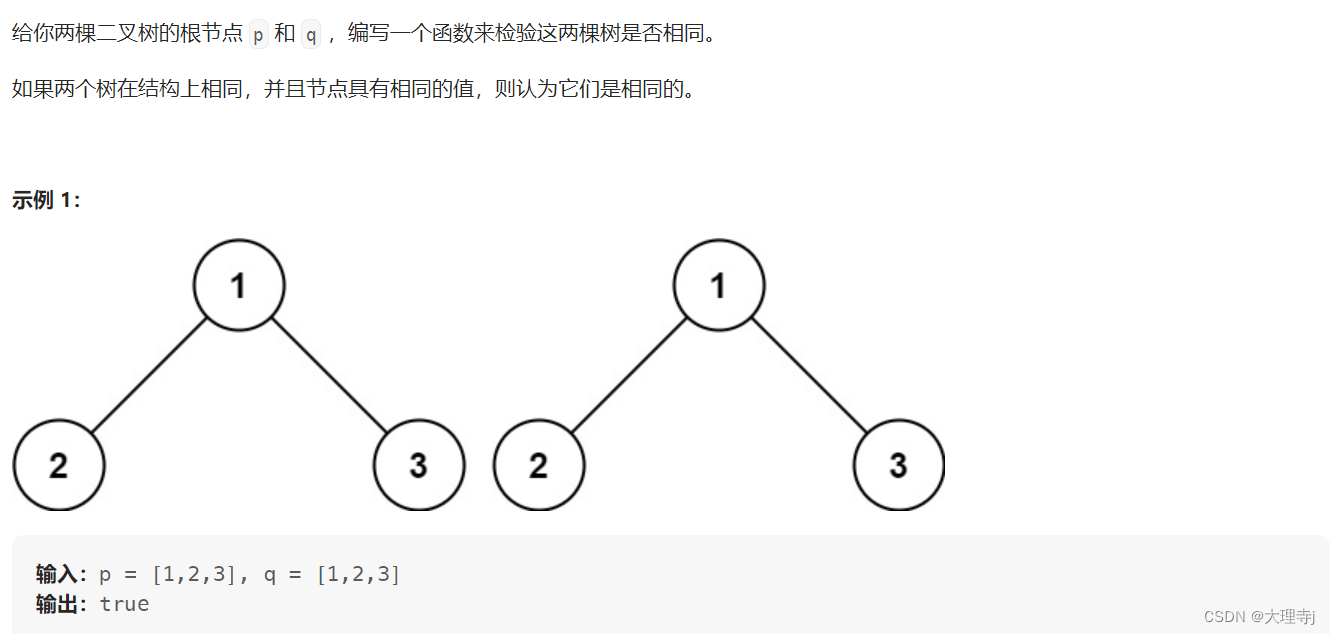
在这里插入图片描述

思路：先比较根结点如果相同就分治下去左右子树作为新的根，反之则返回false
但是要注意几点特殊情况：
一个根节点为空另一个不为空则返回false
两个根节点都是空则返回true

bool isSameTree(struct TreeNode* p, struct TreeNode* q){
    if(p==NULL&&q==NULL)
    {
        return true;
    }
    if(p==NULL||q==NULL)
    {
        return false;
    }
    if(p->val!=q->val)
    {
        return false;
    }
    return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);
}

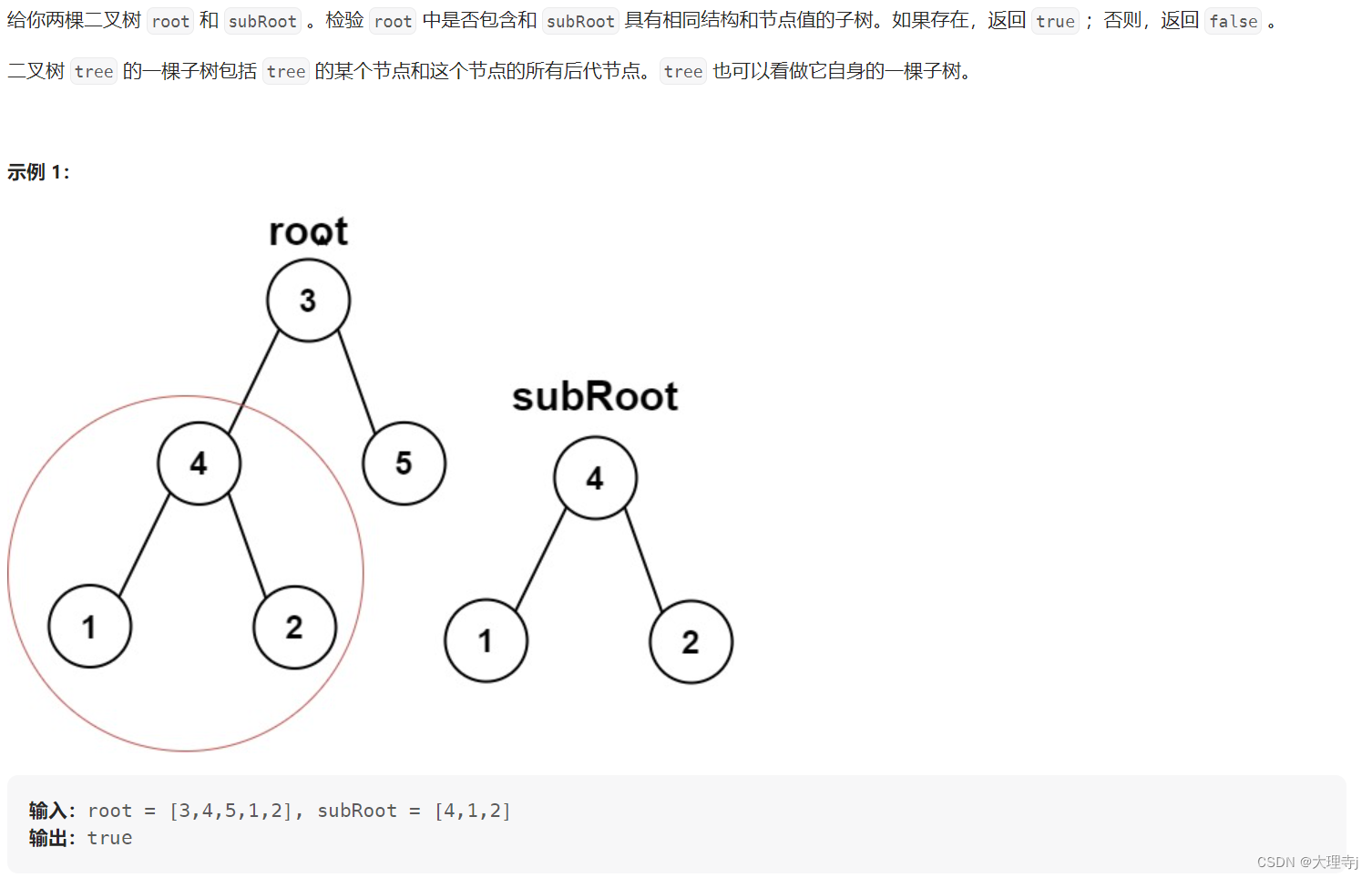
3，另一棵树的子树

链接: 另一棵树的子树

在这里插入图片描述
上面判断两个树是否相等相当于这个问题的子问题，我们只需要依次遍历根结点，左子树，右子树，看是否与subroot是相同的树，如果是就返回true。
注意：如果左子树与subroot相同就不用看右子树了，直接返回true

bool issametree(struct TreeNode* root1,struct TreeNode* root2)
{
    if(root1==NULL&&root2==NULL)
    {
        return true;
    }
    if(root1==NULL||root2==NULL)
    {
        return false;
    }
    if(root1->val!=root2->val)
    {
        return false;
    }
    return issametree(root1->left,root2->left)&&issametree(root1->right,root2->right);
}


bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){
    if(root==NULL)
    {
        return false;
    }
    if(issametree(root,subRoot))
    {
        return true;
    }
    bool ret1=isSubtree(root->left,subRoot);
    if(ret1)
        return ret1;
    bool ret2=isSubtree(root->right,subRoot);
    if(ret2)
        return ret2;
    return false;
}

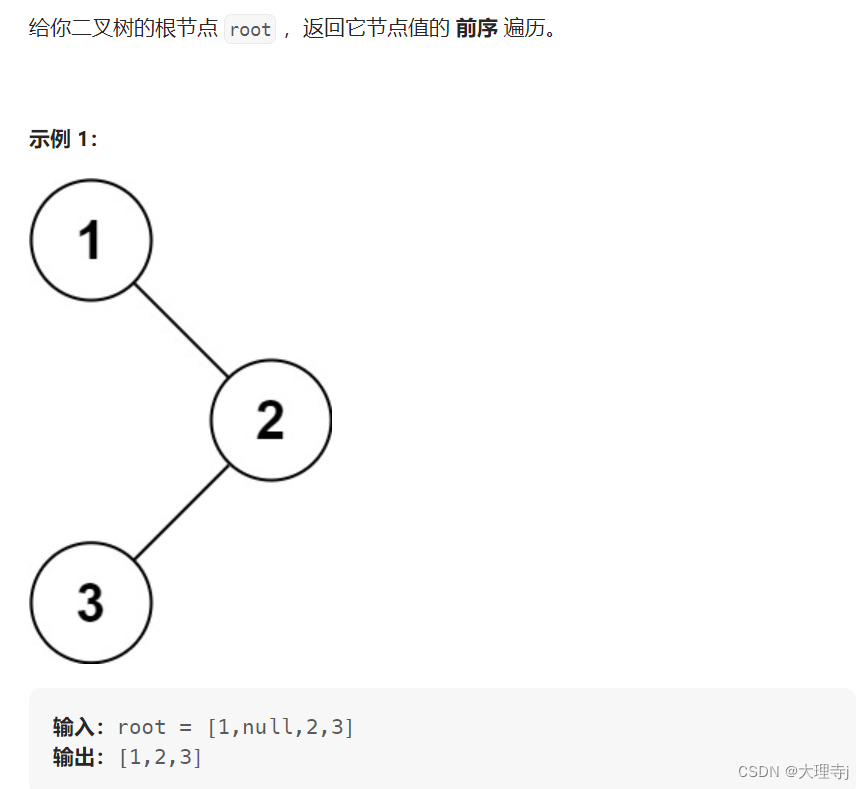
4，二叉树的前序遍历

链接: 二叉树的前序遍历

在这里插入图片描述
OJ题中的前序遍历，是要把遍历的结果放到数组中返回，但是要在传参数的时候要注意，控制数组下标的变量传参时要传指针，否则会有麻烦哦。

void PrevOrder(struct TreeNode* root,int* ret,int* i)
{
    if(root==NULL)
    {
        return ;
    }
    ret[(*i)++]=root->val;
    PrevOrder(root->left,ret,i);
    PrevOrder(root->right,ret,i);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize){
    if(!root)
    {
        *returnSize=0;
        return NULL;
    }
    int* ret=(int*)malloc(sizeof(int)*100);
    int i=0;
    PrevOrder(root,ret,&i);
    *returnSize=i;
    return ret;
}

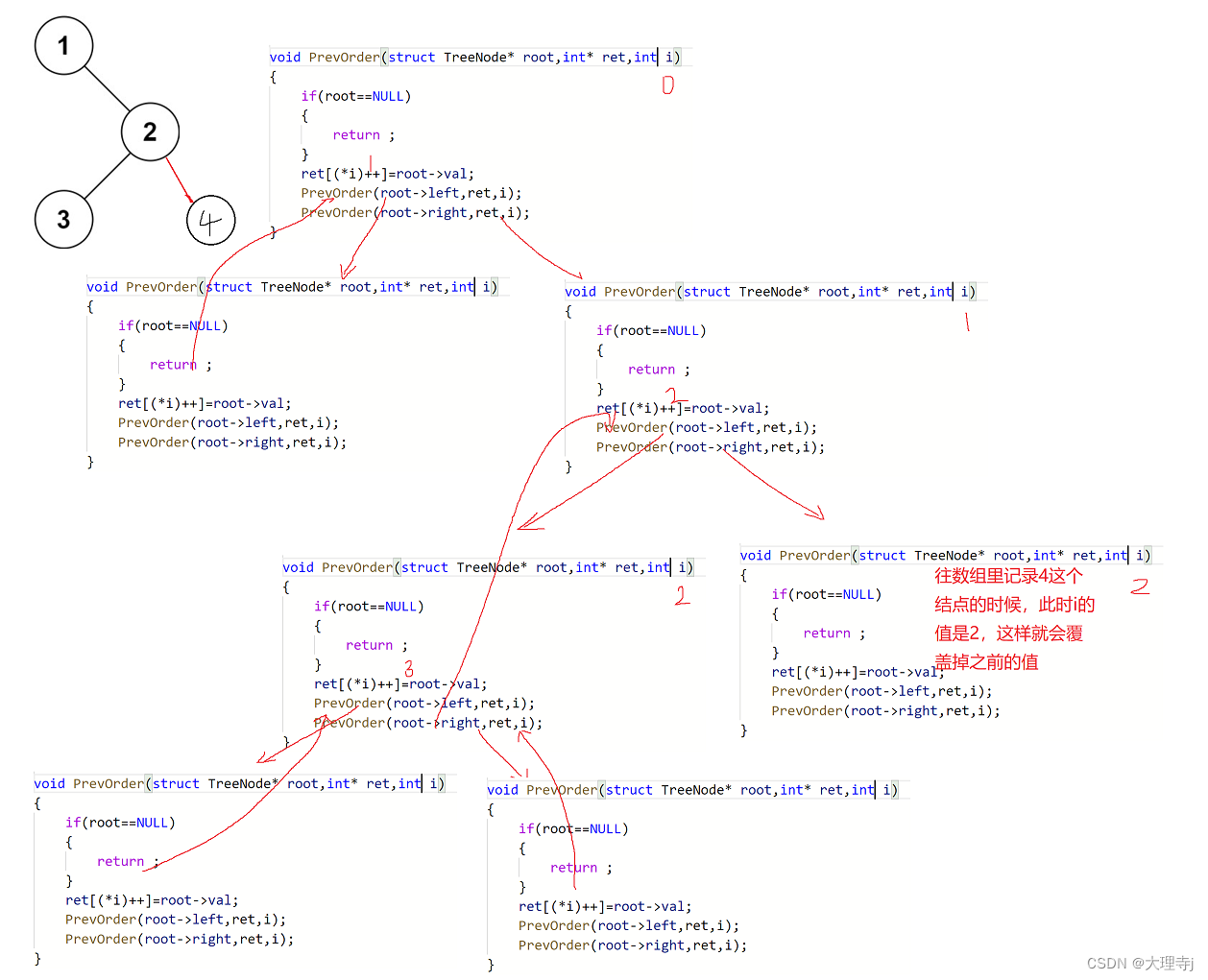
下面来画一下传参时不传指针造成的后果：
在这里插入图片描述
i是记录数组下标的，应该往数组中放一个元素就改变，而向上图中，将3放到数组中后，返回到上一层栈帧此时的i的值仍为2，所以将4放到数组中的时候会把3覆盖掉。
为了防止这样的错误，我们得采用传i的地址，就不会存在上图中的问题。

5，二叉树的中序遍历

链接: 二叉树的中序遍历

中序后序与前序遍历大同小异

 void InOrder(struct TreeNode* root,int* ret,int* i)
{
    if(root==NULL)
    {
        return ;
    }
    InOrder(root->left,ret,i);
    ret[(*i)++]=root->val;
    InOrder(root->right,ret,i);
}
int* inorderTraversal(struct TreeNode* root, int* returnSize){
    if(!root)
    {
        *returnSize=0;
        return NULL;
    }
    int* ret=(int*)malloc(sizeof(int)*100);
    int i=0;
    InOrder(root,ret,&i);
    *returnSize=i;
    return ret;
}

6，二叉树的后序遍历

链接: 二叉树的后序遍历

 void PostOrder(struct TreeNode* root,int* ret,int* i)
{
    if(root==NULL)
    {
        return ;
    }
    PostOrder(root->left,ret,i);
    PostOrder(root->right,ret,i);
    ret[(*i)++]=root->val;
}

int* postorderTraversal(struct TreeNode* root, int* returnSize){
    if(!root)
    {
        *returnSize=0;
        return NULL;
    }
    int* ret=(int*)malloc(sizeof(int)*100);
    int i=0;
    PostOrder(root,ret,&i);
    *returnSize=i;
    return ret;
}

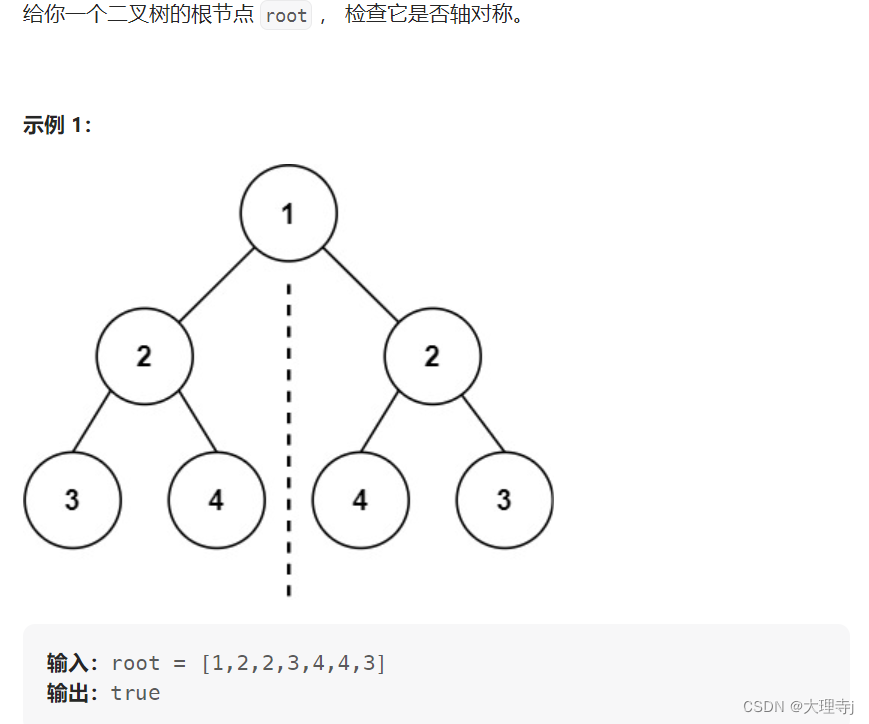
7，对称二叉树

链接: 对称二叉树

在这里插入图片描述
此题与判断两棵树是否相同，非常类似，只需稍加修改即可。
判断两个数是否相同，先判断根结点，再判断root1的左子树与root2的左子树，而对称二叉树只需对比root1的左子树与root2的右子树，这样交叉对比就可以了。

bool issametree(struct TreeNode* root1,struct TreeNode* root2)
{
    if(root1==NULL&&root2==NULL)
    {
        return true;
    }
    if(root1==NULL||root2==NULL)
    {
        return false;
    }
    if(root1->val!=root2->val)
    {
        return false;
    }
    return issametree(root1->left,root2->right)&&issametree(root1->right,root2->left);
}
bool isSymmetric(struct TreeNode* root){
    if(root==NULL)
    {
        return true;
    }
    return issametree(root->left,root->right);
}

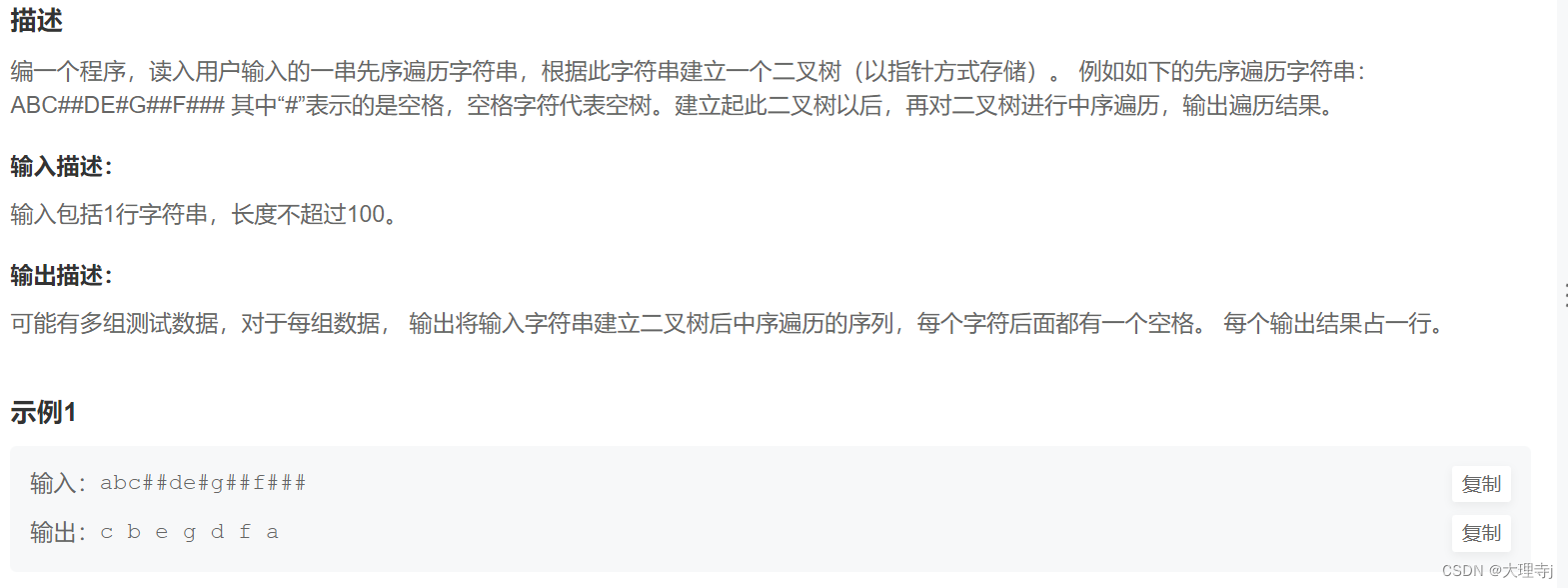
8，二叉树的建立及遍历

链接: 二叉树的建立及遍历

在这里插入图片描述
根据给定的输入字符串，我们先创建根结点，再创建左右子树，如果字符是‘#’就返回NULL。
注意：传数组下标i的时候，也要传地址，与上面讲过的问题一样。

#include <stdio.h>
#include<stdlib.h>

struct TreeNode
{
    char val;
    struct TreeNode* left;
    struct TreeNode* right;
};
struct TreeNode* TreeCreate(char* str,int* pi)
{
    if(str[*pi]=='\0')
    {
        return NULL;
    }
    if(str[*pi]=='#')
    {
        (*pi)++;
        return NULL;
    }
    struct TreeNode* root=(struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->val=str[(*pi)++];
    root->left=TreeCreate(str,pi);
    root->right=TreeCreate(str,pi);
    return root;
}
void InOrder(struct TreeNode* root)
{
    if(root==NULL)
    {
        return;
    }
    InOrder(root->left);
    printf("%c ",root->val);
    InOrder(root->right);
}
int main() {
    
    char str[100];
    scanf("%s",str);
    int pi=0;
    struct TreeNode* ret=TreeCreate(str,&pi);
    InOrder(ret);
    return 0;
}

9，判断是否为平衡二叉树

链接: 判断是否为平衡二叉树

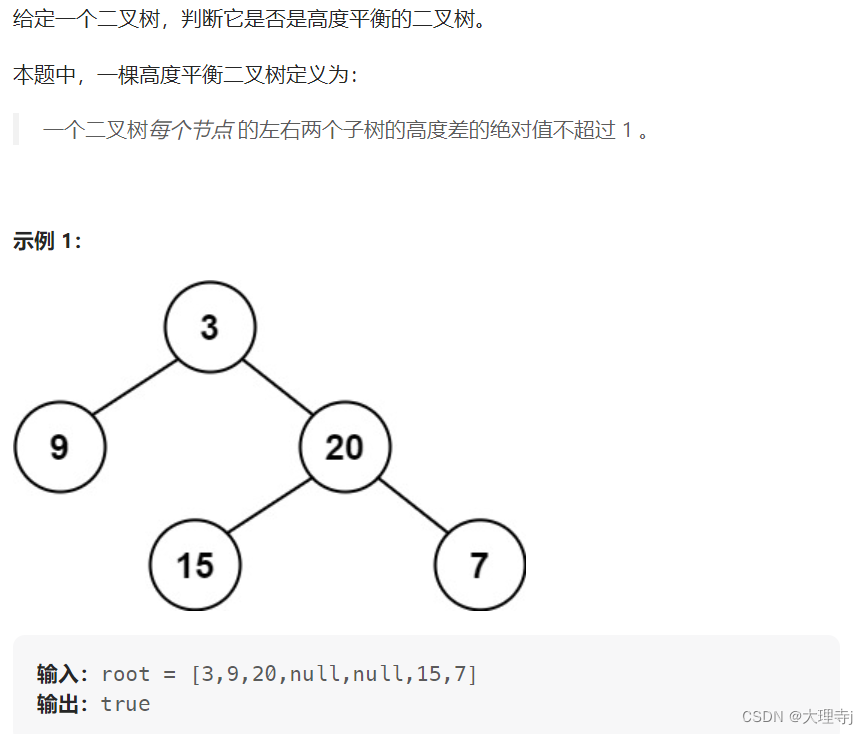
在这里插入图片描述

这个问题实质就是求二叉树高度函数的复用，每次都判断一下左右子树的高度差，如果大于1就返回false。

int TreeHeight(struct TreeNode* root)
{
    if(root==NULL)
    {
        return 0;
    }
    int HL=TreeHeight(root->left);
    int HR=TreeHeight(root->right);
    return HL>HR ? HL+1:HR+1;
}
bool isBalanced(struct TreeNode* root){
    if(root==NULL)
    {
        return true;
    }
    int HL=TreeHeight(root->left);
    int HR=TreeHeight(root->right);
    if(abs(HL-HR)>1)
    {
        return false;
    }
    return isBalanced(root->left)&&isBalanced(root->right);
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/45809.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

m基于NSGAII优化算法的微网系统的多目标优化规划matlab仿真

m基于NSGAII优化算法的微网系统的多目标优化规划matlab仿真

目录 1.算法描述 2.仿真效果预览 3.MATLAB核心程序 4.完整MATLAB 1.算法描述 NSGA-II是基于的非支配排序的方法,在NSGA上进行改进&#xff0c;也是多目标进化优化领域一个里程碑式的一个算法。 NSGA-Ⅱ算法是 Srinivas 和 Deb 于 2000 年在 NSGA 的基础上提出的&#xff0c…
阅读更多...
社区系统项目复盘-3

社区系统项目复盘-3

文章目录过滤敏感词发布帖子帖子详情添加评论私信列表发送私信统一处理异常统一记录日志基于Springboot的核心功能实现 包括自定义前缀树过滤敏感词&#xff1b;使用异步请求的方式发布帖子&#xff1b;查看帖子详情&#xff1b;添加评论时需要同时增加评论的数据和修改帖子的评…
阅读更多...
电源设备设计

电源设备设计

目录 一、通信电源概述 &#xff08;1&#xff09; &#xff08;2&#xff09;通信电源系统组成 &#xff08;3&#xff09;通信电源供电方式 集中供电示意图 分散供电示意图 USP供电示意图 二、交流供电系统设计 1、交流供电--市电引入 交流低压供电示意图 2、交流供电--UPS &…
阅读更多...
Innodb是如何运转的

Innodb是如何运转的

Innodb是如何运转的Innodb体系架构后台线程Master ThreadIO ThreadPurge ThreadPage Cleaner Thread内存缓存池LRU ListFree Listunzip_LRUflush list重做日志缓冲(redo log buffer)额外的内存池checkpoint技术Sharp CheckpointFuzzy CheckpointMaster Thread的工作方式Innodb …
阅读更多...
SparkMlib 之逻辑回归及其案例

SparkMlib 之逻辑回归及其案例

文章目录什么是逻辑回归&#xff1f;逻辑回归的优缺点逻辑回归示例——预测回头客逻辑回归示例——预测西瓜好坏逻辑回归示例——预测垃圾邮件什么是逻辑回归&#xff1f; 逻辑回归是一种流行的预测分类响应的方法。它是预测结果概率的广义线性模型的特例。在逻辑回归中&#…
阅读更多...
EasyRecovery2022中文版电脑端数据恢复软件

EasyRecovery2022中文版电脑端数据恢复软件

EasyRecovery2023数据恢复软件是一款文件恢复软件&#xff0c;能够恢复内容类型非常多&#xff0c;包括办公文档、文件夹、电子邮件、照片、音频等一些常用文件类型都是可以进行恢复&#xff0c;操作非常简单&#xff0c;只需要将存储设备连接到电脑上&#xff0c;运行EasyReco…
阅读更多...
【全志T113-S3_100ask】16-1 linux系统驱动四线电阻屏（tpadc、tslib）

【全志T113-S3_100ask】16-1 linux系统驱动四线电阻屏（tpadc、tslib）

【全志T113-S3_100ask】16-1 linux系统使用TPADC驱动四线电阻屏&#xff08;rtp、tslib&#xff09;&#xff08;一&#xff09;背景&#xff08;二&#xff09;焊接鬼才&#xff08;三&#xff09;解析input上报事件&#xff08;四&#xff09;C语言解析input上报事件&#xf…
阅读更多...
大数据技术——Flume简介安装配置使用案例

大数据技术——Flume简介安装配置使用案例

文章目录1. Flume 概述1.1 Flume简介1.2 Flume的特点1.3 Flume的基础架构2. Flume安装配置2.1 下载地址2.2 安装部署3. Flume 使用案例3.1 实时监控单个追加文件3.2 实时监控目录下多个新文件3.3 实时监控目录下的多个追加文件1. Flume 概述 1.1 Flume简介 Flume是一种可配置、…
阅读更多...
【Linux】Linux的环境变量（PATH、env、子进程继承环境变量等）

【Linux】Linux的环境变量（PATH、env、子进程继承环境变量等）

文章目录环境变量1、从一个小案例认识环境变量PATH2、常用的环境变量相关指令与系统调用3、子进程如何继承环境变量的&#xff1f;4、测试其它环境变量环境变量 1、从一个小案例认识环境变量PATH 我们在shell中通过file查看文件信息&#xff0c;看到我们常使用的指令都是可执…
阅读更多...
C++ 类的静态成员详解

C++ 类的静态成员详解

目录 前言 一、类的静态成员 1.static关键字 2.静态成员变量 3.静态成员函数 二、程序样例 1.程序演示 2.程序截图 总结 前言 本文记录C中 static 修饰类成员成为静态成员&#xff0c;其中包括静态成员类别、作用和程序演示。 嫌文字啰嗦的可直接跳到最后的总结。 一、类的静…
阅读更多...
特征提取 - 骨架、中轴和距离变换

特征提取 - 骨架、中轴和距离变换

目录 1. 介绍 骨架 skeleton 中轴变换 Medial axis transformation 距离变换 distance transform 2. 距离变换的代码实现 distanceTransform 函数介绍 normalize 函数介绍 取局部最大值 完整代码 3. comparation 1. 介绍 骨架 skeleton 骨架的定义&#xff1a;就是…
阅读更多...
【毕业设计】33-基于单片机的直流电机的转速检测与控制设计（原理图工程+PCB工程+源代码工程+仿真工程+答辩论文）

【毕业设计】33-基于单片机的直流电机的转速检测与控制设计（原理图工程+PCB工程+源代码工程+仿真工程+答辩论文）

typora-root-url: ./ 【毕业设计】33-基于单片机的直流电机的转速检测与控制设计&#xff08;原理图工程PCB工程源代码工程仿真工程答辩论文&#xff09; 文章目录typora-root-url: ./【毕业设计】33-基于单片机的直流电机的转速检测与控制设计&#xff08;原理图工程PCB工程源…
阅读更多...
盘点国内主流数字孪生厂商！你了解几家？

盘点国内主流数字孪生厂商！你了解几家？

在国内&#xff0c;主流的数字孪生解决方案厂商包括华龙迅达、精航伟泰、羚数智能、力控科技、华力创通、同元软控、优也科技、51world、卡奥斯、摩尔元数、易知微、木棉树软件等。由于中国数字孪生市场仍处于早期发展阶段&#xff0c;且受限于建模、仿真和基于数据融合的数字线…
阅读更多...
基于单RGB相机的全新三维表示方法｜NeurIPS 2022

基于单RGB相机的全新三维表示方法｜NeurIPS 2022

随着深度学习的发展&#xff0c;基于单张RGB图像的人体三维重建取得了持续进展。 但基于现有的表示方法&#xff0c;如参数化模型、体素栅格、三角网格和隐式神经表示&#xff0c;难以构筑兼顾高质量结果和实时速度的系统。 针对上述问题&#xff0c;天津大学团队联合清华大学…
阅读更多...
Linux用户管理

Linux用户管理

文章目录一. 引子二. 用户管理1. 用户切换2. 注销用户3. 添加用户4. 设置用户密码5. 删除用户6. 查询用户信息三. 用户组管理1. 新增用户组2. 新增用户时添加组3. 修改用户的组四. 用户和组相关文件1. /etc/passwd2. /etc/shadow3. /etc/group一. 引子 Linux是一个多用户、多任…
阅读更多...
【JavaScript作用域】

【JavaScript作用域】

JavaScript作用域1 本节目标2 作用域2.1 作用域概述2.2 全局作用域2.3 局部作用域3 变量的作用域3.1 变量作用域的分类3.2 全局变量3.3 局部变量3.4 从执行效率看全局变量与局部变量3.5 JS没有块级作用域4 作用域链1 本节目标 说出JavaScript的两种作用域区分全局变量和局部变…
阅读更多...
TinyML：是否是FPGA在人工智能方面的最佳应用？

TinyML：是否是FPGA在人工智能方面的最佳应用？

TinyML 也是机器学习的一种&#xff0c;他的特点就是缩小深度学习网络可以在微型硬件中使用&#xff0c;主要应用在智能设备上。超低功耗嵌入式设备正在“入侵”我们的世界&#xff0c;借助新的嵌入式机器学习框架&#xff0c;它们将进一步推动人工智能驱动的物联网设备的普及。…
阅读更多...
机器学习：一文从入门到读懂PCA（主成分分析）

机器学习：一文从入门到读懂PCA（主成分分析）

深度学习&#xff1a;PCA白化前置知识内积的几何意义基基变换不同基下的向量变换逆矩阵不同基下的空间变换方差协方差协方差矩阵协方差矩阵对角化特征值分解、空间变换主成分分析&#xff08;PCA&#xff09;两个原则公式推导求解流程代码实现PCA的优缺点优点缺点前置知识 维度…
阅读更多...
【测试沉思录】18.如何测试微信小程序？

【测试沉思录】18.如何测试微信小程序？

作者&#xff1a;雷远缘 编辑&#xff1a;毕小烦 一. 先知道小程序是什么 啥是小程序&#xff1f; “小程序是一种不需要下载安装即可使用的应用&#xff0c;它实现了应用 “触手可及” 的梦想&#xff0c;用户扫一扫或者搜一下即可打开应用。也体现了 “用完即走” 的理念&am…
阅读更多...
[附源码]Python计算机毕业设计SSM基于Java的民宿运营管理网站（程序+LW)

[附源码]Python计算机毕业设计SSM基于Java的民宿运营管理网站（程序+LW)

环境配置&#xff1a; Jdk1.8 Tomcat7.0 Mysql HBuilderX&#xff08;Webstorm也行&#xff09; Eclispe&#xff08;IntelliJ IDEA,Eclispe,MyEclispe,Sts都支持&#xff09;。 项目技术&#xff1a; SSM mybatis Maven Vue 等等组成&#xff0c;B/S模式 Maven管理等…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023