六、证明:一个算法的运行时间为θ(g(n))当且仅当其最坏情况运行时间为O(g(n)),且其最好情况运行时间为Ω(g(n)) 。
文心一言:

chatgpt:
要证明「一个算法的运行时间为θ(g(n))当且仅当其最坏情况运行时间为O(g(n)),且其最好情况运行时间为Ω(g(n))」,需要证明两个方向:
-
如果算法的运行时间为θ(g(n)),则它的最坏情况运行时间为O(g(n)),且最好情况运行时间为Ω(g(n))。
-
如果算法的最坏情况运行时间为O(g(n)),且最好情况运行时间为Ω(g(n)),则它的运行时间为θ(g(n))。
证明:
(1)首先证明第一部分,即如果算法的运行时间为θ(g(n)),则它的最坏情况运行时间为O(g(n)),且最好情况运行时间为Ω(g(n))。
根据定义,如果算法的运行时间为θ(g(n)),则存在正常数 c1 和 c2,使得对于足够大的 n,有下面的不等式成立:
c1 * g(n) <= T(n) <= c2 * g(n)
其中,T(n) 表示算法在 n 大小的输入上的运行时间。由此可以推出:
- 当 n 趋近于无穷大时,T(n) 的增长率是与 g(n) 相同的。
- 存在正常数 k1 和 k2,使得对于足够大的 n,有 k1 * g(n) <= T(n) 和 T(n) <= k2 * g(n)。
接下来分别证明最坏情况和最好情况的复杂度。
对于最坏情况复杂度,由定义可知该复杂度不超过运行时间的上界。因此,如果 T(n) = O(g(n)),则最坏情况下的复杂度也是 O(g(n))。
对于最好情况复杂度,根据第一个性质,当 n 趋近于无穷大时,T(n) 的增长率是与 g(n) 相同的。因此,最好情况下的复杂度为 Ω(g(n))。
综上所述,算法的运行时间为θ(g(n))时,它的最坏情况运行时间为O(g(n)),且最好情况运行时间为Ω(g(n))。
(2)然后证明第二部分,即如果算法的最坏情况运行时间为O(g(n)),且最好情况运行时间为Ω(g(n)),则它的运行时间为θ(g(n))。
由于最坏情况和最好情况的复杂度都分别受到 g(n) 上界和下界的限制,因此算法的复杂度必然介于两者之间。具体而言,存在正常数 c3 和 c4,使得对于足够大的 n,有下面的不等式成立:
c3 * g(n) <= T(n) <= c4 * g(n)
因此,算法的复杂度为θ(g(n))。
综上所述,一个算法的运行时间为θ(g(n))当且仅当其最坏情况运行时间为O(g(n)),且其最好情况运行时间为Ω(g(n))。

七、证明:o(g(n)) ∩ ω(g(n)) 为空集。
文心一言:

chatgpt:
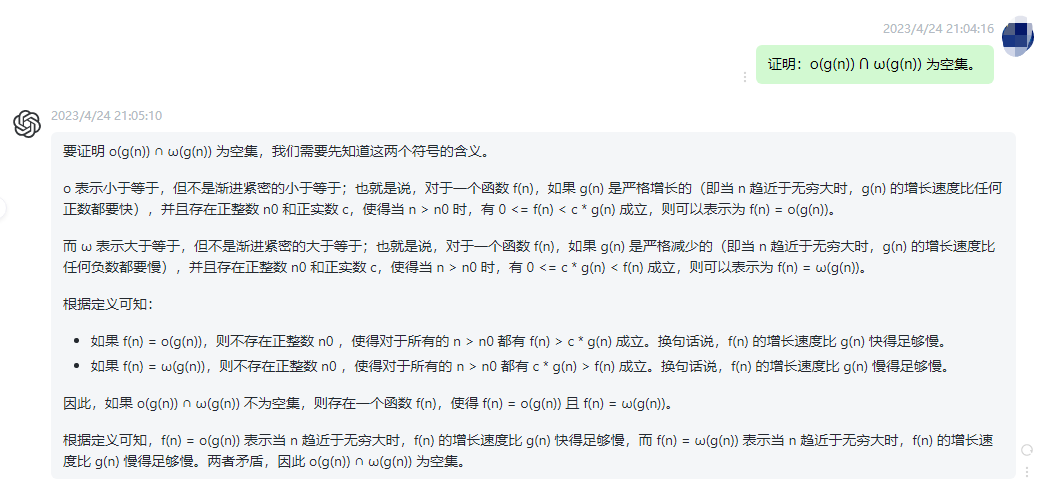
要证明 o(g(n)) ∩ ω(g(n)) 为空集,我们需要先知道这两个符号的含义。
o 表示小于等于,但不是渐进紧密的小于等于;也就是说,对于一个函数 f(n),如果 g(n) 是严格增长的(即当 n 趋近于无穷大时,g(n) 的增长速度比任何正数都要快),并且存在正整数 n0 和正实数 c,使得当 n > n0 时,有 0 <= f(n) < c * g(n) 成立,则可以表示为 f(n) = o(g(n))。
而 ω 表示大于等于,但不是渐进紧密的大于等于;也就是说,对于一个函数 f(n),如果 g(n) 是严格减少的(即当 n 趋近于无穷大时,g(n) 的增长速度比任何负数都要慢),并且存在正整数 n0 和正实数 c,使得当 n > n0 时,有 0 <= c * g(n) < f(n) 成立,则可以表示为 f(n) = ω(g(n))。
根据定义可知:
- 如果 f(n) = o(g(n)),则不存在正整数 n0 ,使得对于所有的 n > n0 都有 f(n) > c * g(n) 成立。换句话说,f(n) 的增长速度比 g(n) 快得足够慢。
- 如果 f(n) = ω(g(n)),则不存在正整数 n0 ,使得对于所有的 n > n0 都有 c * g(n) > f(n) 成立。换句话说,f(n) 的增长速度比 g(n) 慢得足够慢。
因此,如果 o(g(n)) ∩ ω(g(n)) 不为空集,则存在一个函数 f(n),使得 f(n) = o(g(n)) 且 f(n) = ω(g(n))。
根据定义可知,f(n) = o(g(n)) 表示当 n 趋近于无穷大时,f(n) 的增长速度比 g(n) 快得足够慢,而 f(n) = ω(g(n)) 表示当 n 趋近于无穷大时,f(n) 的增长速度比 g(n) 慢得足够慢。两者矛盾,因此 o(g(n)) ∩ ω(g(n)) 为空集。