基本概念

在混淆电路框架下，任意功能函数可被表示为一个与门和异或门组成的布尔电路，协议的参与方由生成方（Garbler）和计算方（Evaluator）组成。
**大致的流程：**生成方生成密钥并加密查找表，计算方在未知密钥和明文之间的关系的条件下解密查找表。

1. 混淆：生成方进行混淆操作
   1. **选择随机密钥：**一个门电路其实就是一个真值表，对于每一个门电路的真值表，生成方首先对每一个输入/输出线上的真值产生一个随机数。这样一来，每一个输入/输出线上的真值就与一个随机数相对应。
   2. **洋葱加密：**然后，生成方对于每一个输出线上的真值所对应的随机数，使用相应输入线上的真值所对应的两个随机数对其进行加密。
   3. **随机置换：**在完成这些加密操作后，生成方对产生的所有密文进行随机置乱，产生一个混淆的，或者说加密的真值表，
2. 数据传输（通信）：生成方将混淆后的真值表连同对应自己一方输入的随机数发给计算方。然后计算方通过OT协议去向生成方索取自己一方的输入随机数
3. **计算方解码表：**计算方对混淆真值表进行解密，得到唯一正确的、与输出真值相对应的随机数。
4. **公布结果：**当计算完最后一个电路得到最终的结果时，计算方可以将该结果发送给生成方，或者发送方将自己选择的随机数发给计算方即可让双方得到最后的结果。

具体流程

考虑诚实好奇模型，以与门为例
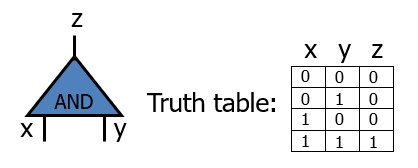
与门的真值表如下

混淆

选择随机密钥

首先是生成方为输入和输出的每个线路都选择两个随机密钥用于代表0和1，即2*3=6个密钥，替换到原来的真值表中的0和1

洋葱式加密

为了使得计算方拥有在拥有一对密钥的时候，只能打开（解密）查找表中的一条数据（一行数据），而无法获取其他的信息，且单独使用$k_x$和$k_y$都无法获取任何信息，甚至不能够判断某个密文是否是使用$k_x$或$k_y$得到的。由此，采用洋葱式的加密方法，如下

随机置换（混淆）

生成方随机打乱真值表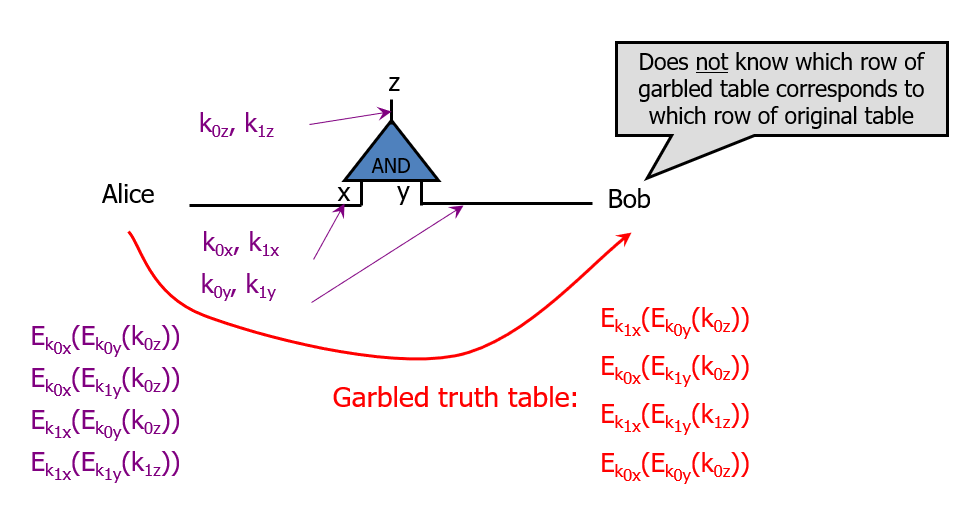

通信

生成方将已经混淆好的真值表和自己输入所对应的密钥给计算方，此时由于密钥是随机数，所以计算方是不知道哪一个随机数代表的是0或者1。在拿到第一个生成方输入部分的密钥之后，计算方还想要拿到第二个计算方自己的输入部分的密钥，但不能让生成方知道自己想获取的密钥是哪一个，这里就需要采用不经意传输协议（OT）最终，计算方持有混淆的真值表，生成方的输入和自己的输入共三个部分。

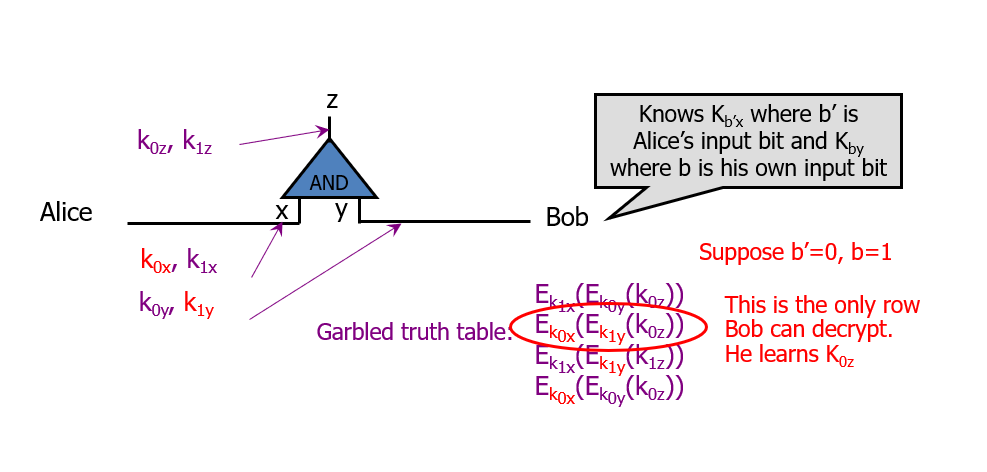
解密计算

计算方通过上述三个部分就可以计算出输出电路的结果，，但此时的输出是也是一个随机数，所以计算方也不知道这个随机数代表的是0还是1。
计算方如何知道自己应该解密真值表的哪一条呢？

1. **思路一，编码附加信息：**在真值表的每一个加密条目的中编码一些附加信息，如$\sigma$个0。如果解密了错误的行，那么解密结果的末尾仅有很低的概率如$(p=\frac{1}{2^{\sigma }})$包含$\sigma$个0。以此来判断是否解密成功。显然这个方案效率很低，平均要解密查找真值表一半的条目。
2. **思路二，标识置换：**来源于Beaver等人在1990年提出来的解决方案。假设持有的参与方$P1$持有私有值$x\in X$，参与方$P2$持有私有值$y\in Y$，开始选择足够长的密钥 k x ∈ R { 0 , 1 } k k_{x}\in_R \{0,1\}^k kx​∈R​{0,1}k和 k x ∈ R { 0 , 1 } k k_{x}\in_R \{0,1\}^k kx​∈R​{0,1}k对每一个私有值进行加密，选择密钥的一部分（第一个密钥的后$\lceil \log |X|\rceil$和第二个密钥的后$\lceil \log |Y|\rceil$个比特）作为查找表的置换标识。标识密钥应该用于加密哪行密文，根据置换标识对加密后的查找表进行相应的替换。为了保证密钥的长度，一般将这种标识直接加在密钥后面，同时需要保证置换标识不会在两个密钥空间中出现冲突。

公布结果

最后计算方可以将最终的计算结果给生成方看，生成方就可以通过自己掌握的随机数映射表得到真实的值。也可以生成方发送随机数给计算方。
不发送最终随机数的解决办法
生成方在发送混淆真值表的时候，可以同步发送一个解码表，解码表只将每个输出门对应的随机数映射为对应值，然后又计算方自行查找计算处最终结果。
这只是单个门的计算例子，接着可以以此类推就可以扩展到整个电路。

当前方案

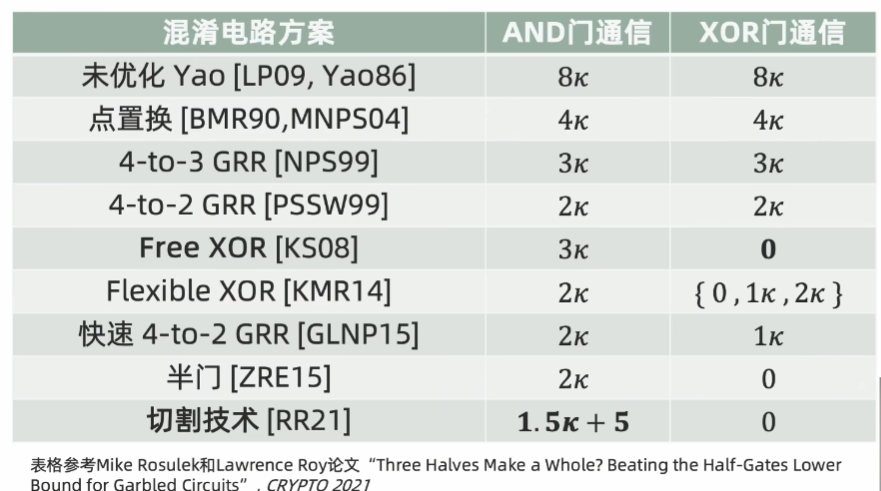
参考

混淆电路介绍（三）混淆电路原理
《实用安全多方计算导论》