之前已经完成了六篇关于时间序列的博客，还没有阅读过的读者请先阅读：

时间序列的数据分析(一):主要成分
时间序列的数据分析(二):数据趋势的计算
时间序列的数据分析(三):经典时间序列分解
时间序列的数据分析(四):STL分解
时间序列的数据分析(五):简单预测法

6. 时间序列的数据分析(六):指数平滑预测法

数据平稳性(Stationarity)

数据平稳性是指时间序列的统计特性如均值、方差、协方差不随时间变化而变化。换句话说，时间序列的均值、方差和协方差随时间保持不变。

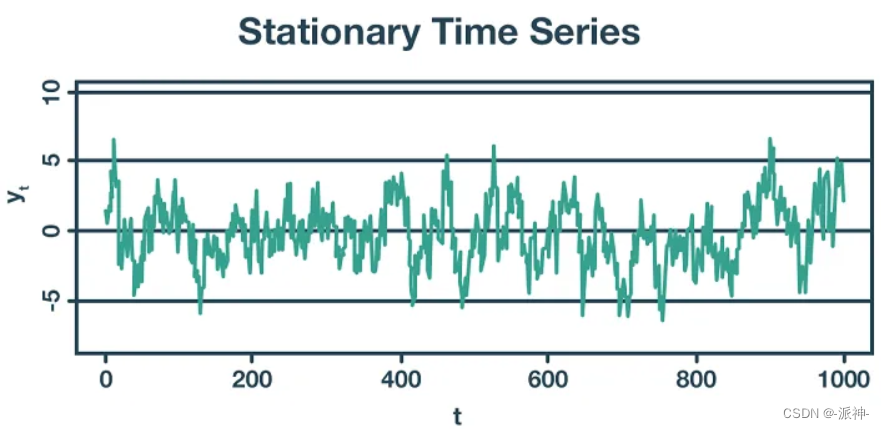
如何评估数据的平稳性: 视觉评估

如果时间序列数据同时具有恒定的均值,方差,协方差这三个特征,那么我们可以认定数据是平稳的,反之数据是非平稳的。因此我们可以通过简单的视觉方法来观察数据的变化规律，从而可以判断出数据是否是平稳：

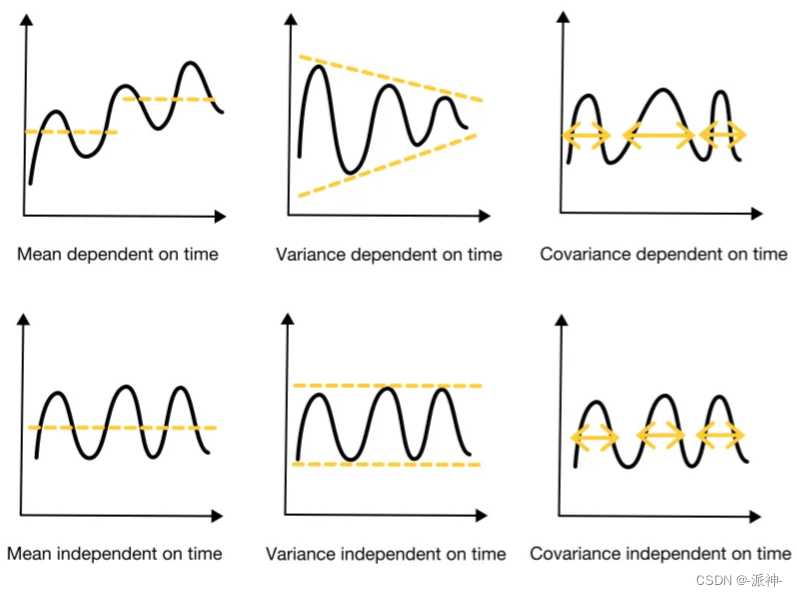
简单计算来识别数据的平稳性

我们大体上可以将时间序列数据分成两半:前半部分和后半部分。并比较前半部分和后半部分的均值、振幅和周期长度。这里振幅对应方差,周期长度对应协方差。

常数均值：数据的前半部分和后半分的均值相似(无需绝对相等)
常数方差: 数据的前半部分和后半分的振幅相似(无需绝对相等)
常数协方差: 数据的前半部分和后半分的周期长度相似(无需绝对相等)

如果时间序列数据同时具有常数均值,常数方差,常数协方差这三个特征,那么我们可以认定数据是平稳的,反之数据是不平稳的。

统计检验来评估平稳性

严格的统计检验来评估数据的平稳性也称为单根检验(unit root test),单根是一种随机趋势，称为“带漂移的随机游走”。由于无法预测随机性，这意味着：

存在单位根：非平稳（不可预测）
没有单位根：平稳

要使用单位根检验来评估平稳性需要使用假设检验：

零假设(Null hypothesis,H0): 时间序列是平稳的（不存在单根）
备择假设 (Alternative hypothesis,H1) :时间序列不平稳的（存在单位根）

注意，这里的H0和H1具体的假设内容并不一定为上述内容为准，也可能正好相反,假设的内容要有具体的检验方法确定的。

然后，将根据统计计算结果评估是否拒绝零假设,如果拒绝H0,则意味着接受H1，反之亦然。

p 值方法：
如果 p 值 > 0.05，则无法拒绝零假设。
如果 p 值 ≤ 0.05，则拒绝零假设。

临界值方法：
如果检验统计量没有临界值那么极端，则无法拒绝零假设。
如果检验统计量比临界值更极端，则拒绝零假设。

注：当 p 值接近显著值（例如，大约 0.05）时，应使用临界值方法 .

常用的单根检验方法

1.Augmented Dicky Fuller Test（ADF检验）

Augmented Dickey-Fuller (ADF) 检验的假设是：

零假设 (H0)：时间序列非平稳的，因为存在单位根（如果 p 值 > 0.05）
备择假设 (H1)：时间序列是平稳的，因为没有单位根（如果 p 值 ≤ 0.05）

在Python中我们可以使用statsmodels包的adfuller方法来实现ADF检验。不过为了检验单根检验结果的有效性,我们事先准备好了两套数据，一个是航空公司历年乘客数量数据，另一个是白噪声数据，这里的乘客数据有着明显的趋势性,所以它是非平稳的,而白噪声数据则是平稳的。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('ggplot')
plt.rc("figure", figsize=(10,4))

#非平稳的航空乘客数据
df=pd.read_csv('passengers.csv').set_index('Period')
df.plot();

# 平稳的白噪声序列
np.random.seed(10)
y= np.random.normal(loc=0,scale=1,size=500)
white_noise = pd.Series(y)
white_noise.plot();

下面我们使用adf来分别检验这两种数据的平稳性。

from statsmodels.tsa.stattools import adfuller

#航空公司乘客数据adf检验
result = adfuller(df["passengers"].values)

print('ADF Statistics: %f' % result[0])
print('p-value: %f' % result[1])
print('Critical values:')
for key, value in result[4].items():
    print('\t%s: %.3f' % (key, value))

print(f'Result: The series is {"not " if result[1] > 0.05 else ""}stationary')

判断标准：

如果P-value <=0.05 并且 test statistic< 1% 的临界值(Critical values) 则拒绝零假设。
如果P-value > 0.05 或者 test statistic> 1% 的临界值(Critical values) 则接接受零假设。

这里我们的P-value为0.99 > 0.05 所以接受零假设,即数据是非平稳的。(adf的零假设为数据是非平稳的)。

#白噪声的adf建议结果
result = adfuller(white_noise.values)
print('ADF Statistics: %f' % result[0])
print('p-value: %f' % result[1])
print('Critical values:')
for key, value in result[4].items():
    print('\t%s: %.3f' % (key, value))
print(f'Result: The series is {"not " if result[1] > 0.05 else ""}stationary')

这里pvale值为0.0<0.05 并且 test statistic值为-23.677<1%的临界值-3.443，所以拒绝H0,接受H1,即数据是平稳的。

2. Kwiatkowski-Phillips-Schmidt-Shin Test (KPSS 检验)

KPSS是用来计算零假设数据是水平或趋势平稳的检验方法。

KPSS 检验的假设是：

零假设 (H0)：时间序列是平稳的，因为没有单位根（如果 p 值 > 0.05）
备择假设 (H1)：时间序列非平稳的，因为存在单位根（如果 p 值 ≤ 0.05）

注意：KPSS检验和ADF检验它们的假设正好相反。

在Python中我们可以使用statsmodels包的kpss方法来实现KPSS检验。在kpss中有一个参数regression,因为航空公司乘客数据是有明显的趋势,看上去是趋势稳定的，因此regression必须设置为“ct”

from statsmodels.tsa.stattools import kpss
# 检验航空乘客数据
statistic, p_value, n_lags, critical_values = kpss(df["passengers"].values,
                                                   regression = "ct");
print(f'KPSS Statistic: {statistic}')
print(f'p-value: {p_value}')
# print(f'num lags: {n_lags}')
print('Critial Values:')
for key, value in critical_values.items():
    print(f'   {key} : {value}')
print(f'Result: The series is {"not " if p_value < 0.05 else ""}stationary')

判断标准：

1.如果P-value <=0.05 并且 test statistic>临界值(Critical values) 则拒绝零假设。
2.如果P-value > 0.05 或者 test statistic<临界值(Critical values) 则接接受零假设。

这里我们的P-value为0.1 > 0.05 所以接受零假设,即数据是平稳的。

#检验白噪声
statistic, p_value, n_lags, critical_values = kpss(white_noise.values)
print(f'KPSS Statistic: {statistic}')
print(f'p-value: {p_value}')
print(f'num lags: {n_lags}')
print('Critial Values:')
for key, value in critical_values.items():
    print(f'   {key} : {value}')
print(f'Result: The series is {"not " if p_value < 0.05 else ""}stationary')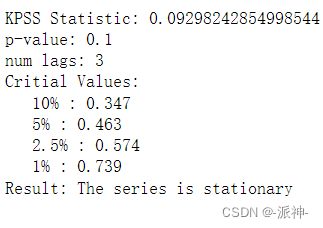

这里白噪声的P-value为0.1 > 0.05 所以接受零假设,即数据是平稳的。

单根检验存在的问题

不同的单根检验方法如adf,kpss等有时候会给出截然相反的结论,这会使人产生困惑，为了确保检验结果的正确性,我们必须要用2种或以上方法同时做检验，下面是2种方法做检验时候会遇到的情况：

情况1：两个测试都得出的结论都是是平稳的，那么数据是平稳的。
情况2: 两个测试都得出的结论都是非平稳的，那么数据是非平稳的。
情况3：ADF 得出非平稳的结论，KPSS 得出平稳的结论，那么数据是趋势平稳。
情况4：ADF 得出平稳的结论，KPSS 得出非平稳的结论，那么数据是差分平稳。

如何处理非平稳的数据

当我们的时间序列时间是非平稳的时候,那么我们可以通过以下方法使数据变的平稳：

差分
通过模型拟合去趋势
对数变换

1.差分

差分是计算两个连续观察值之间的差值。它会使时间序列的均值变得稳定，从而减少了趋势。下面我们拿特斯拉的股票数据来实现差分操作：

#加载特斯拉股票数据
df= pd.read_csv('./data/tsla.csv')
df.date=pd.to_datetime(df.date)

# 对特斯拉股票数据进行差分处理
df['diff_Close']= df['Close'].diff()

#绘图
fig, axs = plt.subplots(2, 1,figsize=(10,8))
axs[0].plot(df.date,df.Close)
axs[0].set_title('Tsla Stock Price')
axs[1].plot(df.date,df.diff_Close)
axs[1].set_title('differencing Tsla Stock Price')
plt.show();

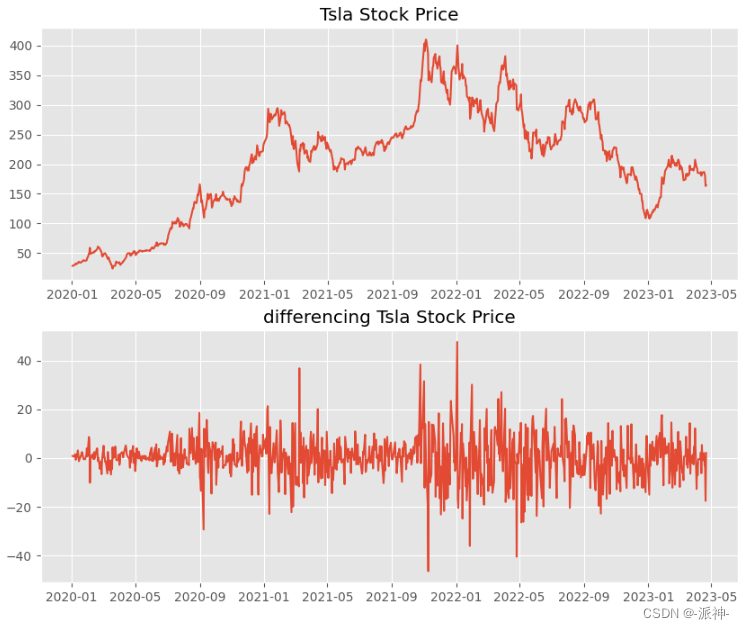
通过对特斯拉股票数据进行一阶差分操作后我们得到了一个类似于白噪声的序列，它近似平稳。有时候如果一阶差分的结果仍然不平稳，那么还可以进行二阶差分操作,但一般不会做二阶以上的差分。

2.通过模型拟合去除趋势

从非平稳时间序列中去除趋势的一种方法是将简单模型（如线性回归）拟合到数据，然后从该拟合中对残差进行建模。

from sklearn.linear_model import LinearRegression

#非平稳的航空乘客数据
df=pd.read_csv('passengers.csv')
df.Period=pd.to_datetime(df.Period)

# 训练线下回归模型 
X = [i for i in range(0, len(df))]
X = np.reshape(X, (len(X), 1))
y = df["passengers"].values
model = LinearRegression()
model.fit(X, y)

# 计算趋势
trend = model.predict(X)

# 去除趋势
df["detrend"] = df["passengers"].values - trend

#绘图
fig, axs = plt.subplots(2, 1,figsize=(10,8))
axs[0].plot(df.Period,df.passengers)
axs[0].set_title('passengers')
axs[1].plot(df.Period,df.detrend)
axs[1].set_title('detrend passengers')
plt.show();

去趋势的方法可以稳定数据的均值,但是均值稳定了并不意味着数据就是平稳的，上述航空乘客数据经过去趋势操作后悔，虽然均值稳定了，但是方差仍然不稳定,那是否可以让让方差也变得稳定呢？

3.对数变换

对数变换可以让时间序列数据的方差变得更加稳定，上述航空公司乘客数据经过去除趋势处理后,均值变得稳定了，但是方差仍然不稳定，因此我们需要做对数变换，让其方差变得稳定。

df=pd.read_csv('passengers.csv')
df.Period=pd.to_datetime(df.Period)
#对数变换
df['log_passengers'] = np.log(df['passengers'].values)

# 训练线下回归模型 
X = [i for i in range(0, len(df))]
X = np.reshape(X, (len(X), 1))
y = df["log_passengers"].values
model = LinearRegression()
model.fit(X, y)

# 计算趋势
trend = model.predict(X)

# 去除趋势
df["detrend_log_passengers"] = df["log_passengers"].values - trend

#绘图
fig, axs = plt.subplots(3, 1,figsize=(10,10))
axs[0].plot(df.Period,df.passengers)
axs[0].set_title('passengers')
axs[1].plot(df.Period,df.log_passengers)
axs[1].set_title('log passengers')

axs[2].plot(df.Period,df.detrend_log_passengers)
axs[2].set_title('detrend log passengers')
plt.show();