牛顿法简介

牛顿法（Newton’s method）是一种常用的优化算法，在机器学习中被广泛应用于求解函数的最小值。其基本思想是利用二次泰勒展开将目标函数近似为一个二次函数，并用该二次函数来指导搜索方向和步长的选择。

牛顿法需要计算目标函数的一阶导数和二阶导数，因此适用于目标函数可二阶可导的情况。在每一步迭代中，牛顿法会根据当前位置的一阶导数和二阶导数，计算出目标函数的二次泰勒展开式，并利用该二次函数的极小值点作为下一步的迭代点。因此牛顿法可以更快地接近最优解，尤其是对于高维函数来说。

但是，牛顿法的计算复杂度比较高，尤其是在高维空间中，需要计算大量的一阶和二阶导数。此外，牛顿法可能会收敛到局部最优解而非全局最优解，因为每一步迭代只能考虑当前位置的局部信息。

牛顿法也有一些改进的方法，如拟牛顿法（quasi-Newton method），它通过建立一个近似目标函数的Hessian矩阵来避免计算Hessian矩阵，提高了计算效率。

牛顿法数学推导

牛顿法是一种迭代方法，用于寻找多元函数的最小值或最大值。具体地，牛顿法利用函数的二阶导数信息来近似函数，并通过迭代求解近似函数的零点来求解原函数的最小值或最大值。

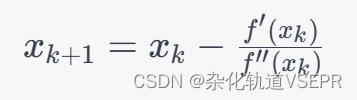
设$f(x)$为一个实值函数，$x_0$为函数$f(x)$的一个初始点，$x_k$为$f(x)$的第$k$次近似解，则牛顿法的迭代公式为：

其中$f^{\prime }(x_k)$和$f^{\prime \prime }(x_k)$分别表示$f(x)$在$x_k$处的一阶导数和二阶导数。

对于求解函数的最小值，牛顿法的停止条件可以选择当函数值的变化小于某个阈值时停止迭代，即：

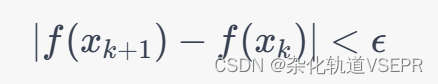
对于求解函数的最大值，牛顿法的停止条件可以选择当函数值的变化小于某个阈值时停止迭代，即：

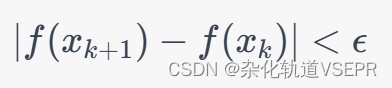
或者选择当函数的一阶导数小于某个阈值时停止迭代，即：

需要注意的是，在实际应用中，牛顿法可能会因为某些点的二阶导数为0或者不存在而导致迭代失败。此外，当函数存在多个局部最小值或最大值时，牛顿法可能会陷入局部最小值或最大值而无法找到全局最小值或最大值。

海森矩阵

海森矩阵是牛顿法的核心之一。在牛顿法中，我们需要用到目标函数的梯度和海森矩阵，其中梯度告诉我们目标函数在某一点上的变化率，而海森矩阵则告诉我们梯度的变化率，即梯度的梯度。通过将海森矩阵加入牛顿法的迭代步骤中，我们可以更准确地确定下一步的搜索方向和步长，从而实现更快的收敛速度。

具体来说，在牛顿法的每次迭代中，我们需要计算目标函数在当前位置的梯度和海森矩阵，然后根据这些信息计算出下一步的搜索方向和步长。具体来说，我们使用海森矩阵的逆矩阵作为Hessian的近似值来计算搜索方向和步长。最终，通过不断迭代，我们可以找到目标函数的最小值点。
海森矩阵（Hessian matrix）是一个函数的二阶偏导数构成的方阵，通常用 $H$ 表示。对于函数 $f(x_1,x_2,\dots ,x_n)$

其中 $\frac{{\partial }^{2}f}{\partial x_i\partial x_j}$ 表示 $f$ 对 $x_i$ 偏导数再对 $x_j$ 偏导数，即 $x_i$ 和 $x_j$ 的二阶偏导数。

在 Python 中可以使用 NumPy 库计算海森矩阵。假设 $f(x_1,x_2)$ 是一个二元函数，则可以定义计算海森矩阵的函数如下：

import numpy as np

def hessian(f, variables):
    """
    Compute the Hessian matrix of a function f with respect to variables.
    """
    n = variables.shape[0]
    hessian = np.zeros((n, n))
    for i in range(n):
        for j in range(i, n):
            hessian[i][j] = f(*variables, i, j)
            hessian[j][i] = hessian[i][j]
    return hessian

代码实现

这段代码的目的是使用牛顿法来优化一个简单的一元二次函数$f(x)=x^3-3x^2$，最终找到它的极小值点。首先在newton函数中定义了牛顿法的迭代公式，其中x_new是新的迭代点，使用原来的点x减去海森矩阵的逆矩阵乘以梯度向量得到。牛顿法中的关键是要计算海森矩阵，所以需要定义一个计算海森矩阵的函数hessian，其中通过二阶偏导数公式计算$f(x)$的二阶导数$h(x)$，也就是海森矩阵。最后，在main函数中调用newton函数并画出优化结果的图像，可以看到牛顿法能够快速地找到函数的极小值点。

import numpy as np
import matplotlib.pyplot as plt

# Define the function to be optimized
def f(x):
    return x ** 3 - 3 * x ** 2

# Define the gradient of the function
def grad(x):
    return 3 * x ** 2 - 6 * x

# Define the Hessian of the function
def hessian(x):
    return np.array([[6 * x - 6]])

# Implement Newton's method
def newton(x, f, grad, hessian, alpha=0.1, max_iter=100):
    for i in range(max_iter):
        x_new = x - alpha * np.linalg.inv(hessian(x)).dot(grad(x))
        if np.abs(f(x_new) - f(x)) < 1e-6:
            break
        x = x_new
    return x_new

# Find the minimum of the function using Newton's method
x0 = 0
x_min = newton(x0, f, grad, hessian)

# Plot the function
x = np.linspace(-1, 3, 100)
y = f(x)
plt.plot(x, y, label='Function')

# Plot the minimum point
plt.plot(x_min, f(x_min), 'ro', label='Minimum')

# Add labels and legend
plt.xlabel('x')
plt.ylabel('y')
plt.legend()

# Show the plot
plt.show()

但是当海森矩阵在某些点上不可逆的时候就会出现计算错误的情况。
海森矩阵不可逆的情况有以下几种：

1.海森矩阵不满秩：在某些点上，海森矩阵可能不是满秩的，这样就会出现不可逆的情况。

2.函数具有平稳点：在平稳点处，海森矩阵为零矩阵，因此不可逆。

3.函数存在鞍点：鞍点是指函数在某一维上是局部最小值，而在另一维上是局部最大值的点。在鞍点处，海森矩阵的特征值有正有负，因此不可逆。

在实际应用中，通常需要对海森矩阵进行调整，使其可逆。一种常见的方法是加入一个正则化项，比如L2正则化，这样可以使海森矩阵始终是正定矩阵，从而保证可逆性。