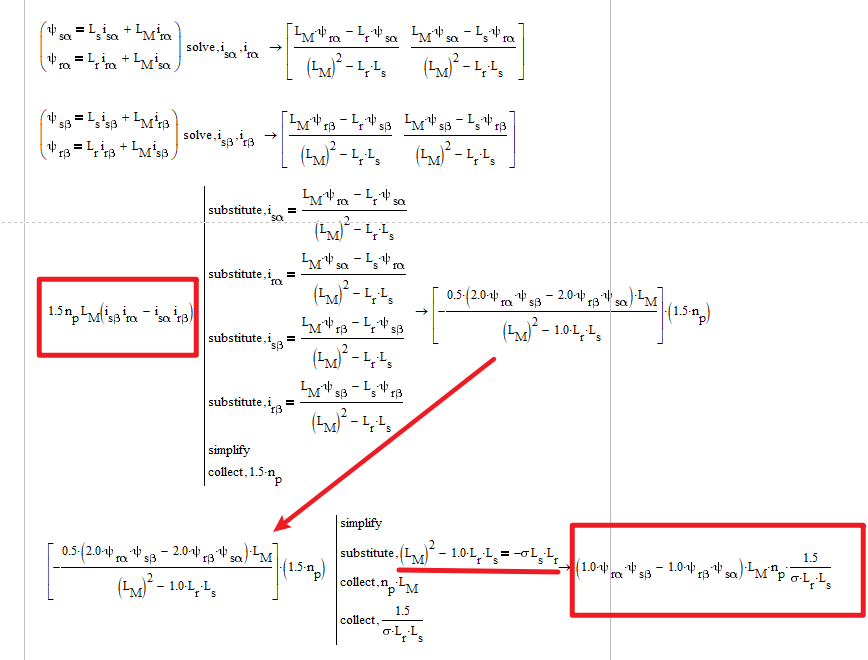
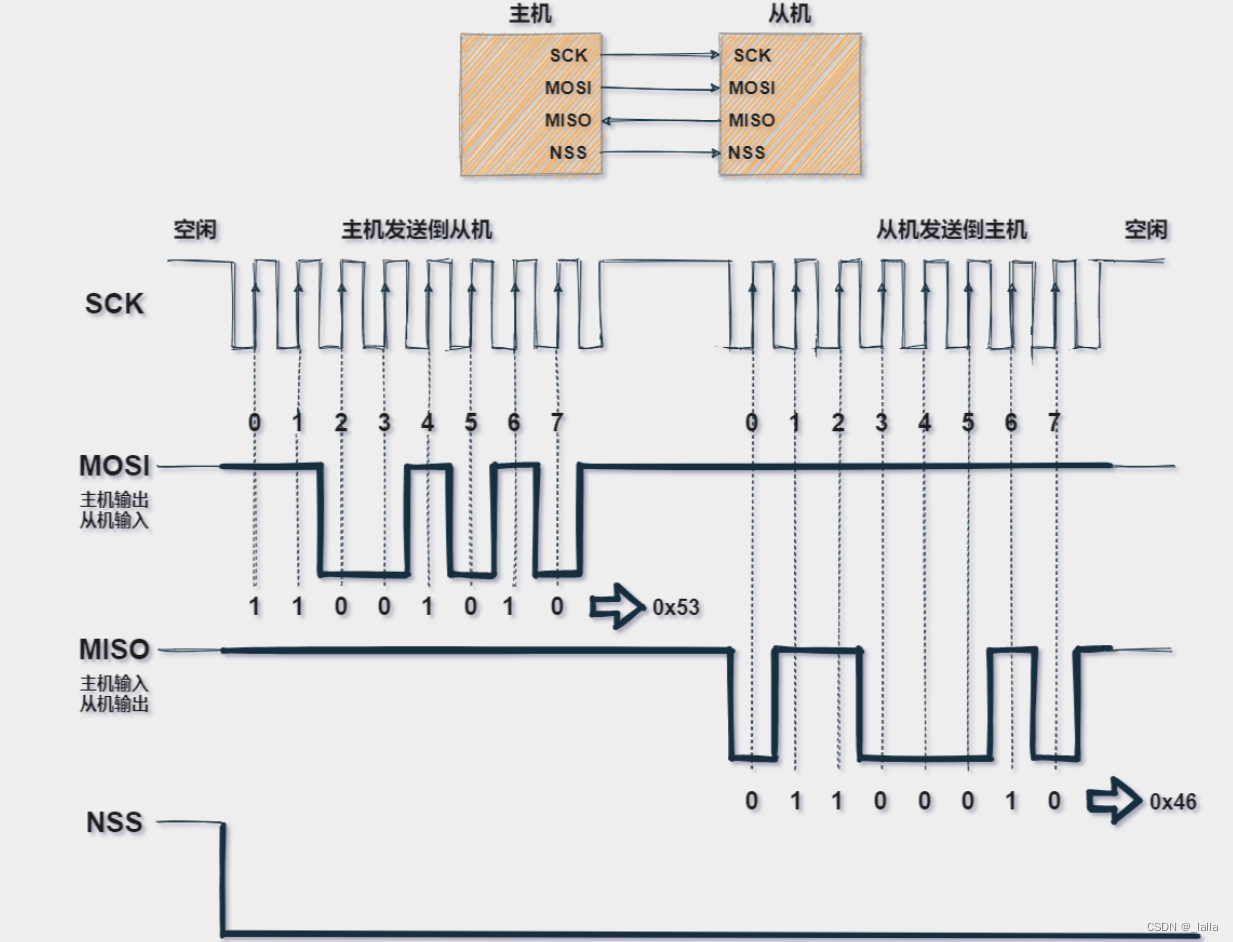
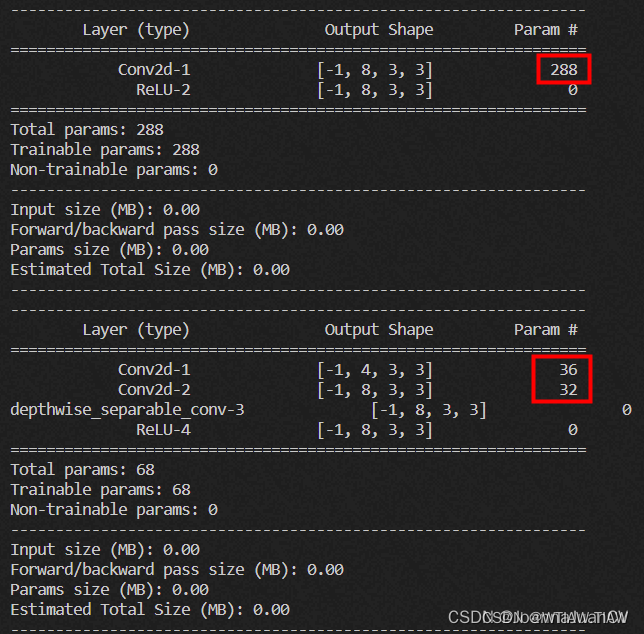
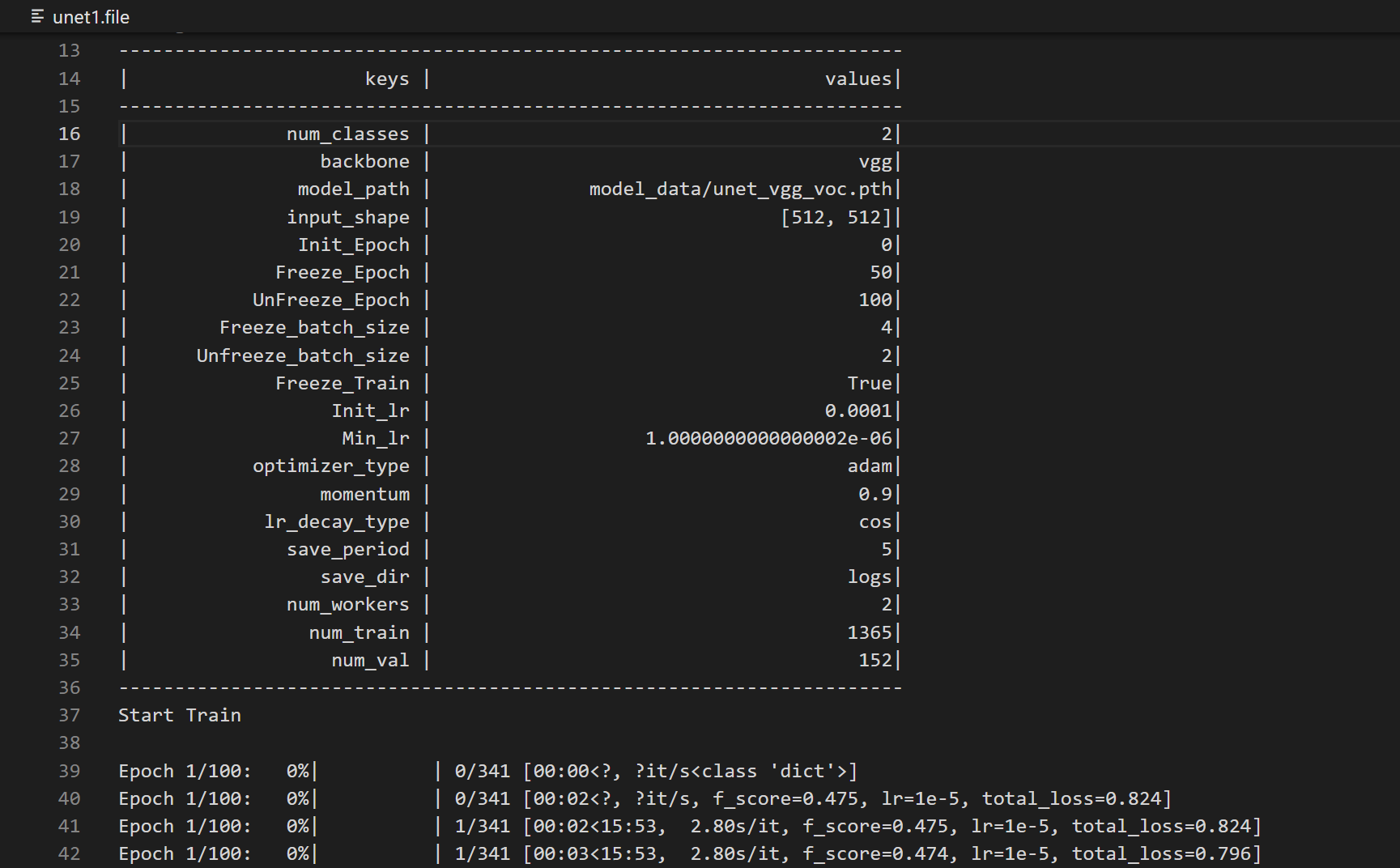
图像的空域滤波：
$I\ast G$
矩阵$I$与一个小矩阵$G$进行卷积

图像的频域滤波：
$F^{-1}[F[I]\times H]$
矩阵$I$的傅里叶变换与同样大小的矩阵$H$进行对应元素相乘，然后将结果通过逆傅里叶变换变换回空域

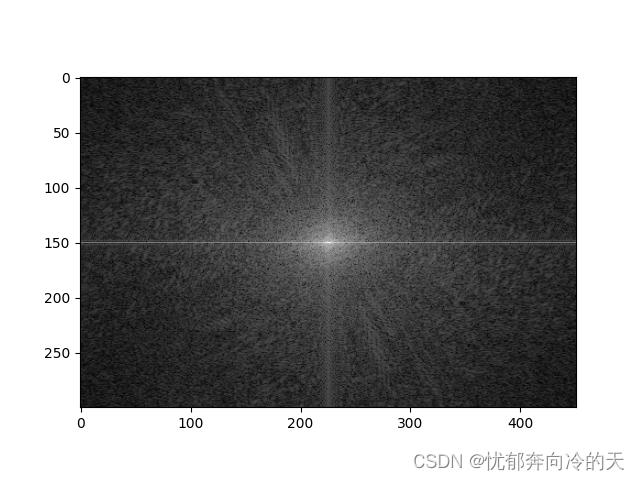
频谱中心化：
图像经过傅里叶变换后，高频在中心，低频在四周。
频谱中心化是把低频放在中心，高频放在四周。
将图像$I(x,y)$乘以$(-1{)}^{x+y}$，再进行傅里叶变换，即可达到频谱中心化。

# -*- coding: utf-8 -*-
"""
@time: 2023-04-22 15:03
@author: leslie lee
"""
from skimage import data, color
import numpy as np
import matplotlib.pyplot as plt


# 读取图片
img = color.rgb2gray(data.cat())
x, y = np.arange(img.shape[1]), np.arange(img.shape[0])
X, Y = np.meshgrid(x, y)
img = img * np.power(-1, X+Y)
plt.imshow(img, cmap='gray')
plt.show()

# 傅里叶变换
img_F = np.fft.fft2(img)
plt.imshow(np.log(1+np.abs(img_F)), cmap='gray')
plt.show()

在此有个疑问：
为什么np.fft.fftshift函数与乘以$(-1{)}^{x+y}$的效果有点不同呢？
未进行频谱中心化

频谱中心化-fftshift函数

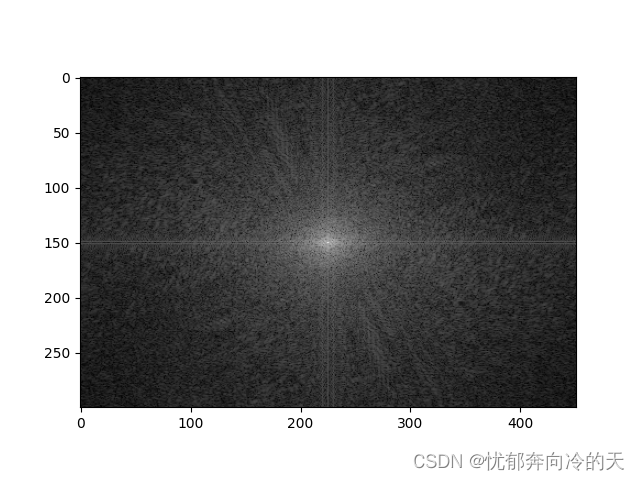
频谱中心化-乘以$(-1{)}^{x+y}$