DFIG控制10-b 双馈发电机的转矩方程推导

接上DFIG控制10： 双馈发电机的动态模型_Fantasy237的博客，DFIG的转矩方程和推导。
（字数限制，只能放在新的一篇博文里了。。）

转矩方程

定子αβ静止坐标系

从三相坐标系下的转矩方程开始，换算定子αβ静止坐标系的转矩方程：
$$\begin{array}{rl}{T}_e& =0.5n_p\left({\mathbf{i}}_r^T\frac{d{\mathbf{L}}_{rs}({\theta }_r)}{d{\theta }_r}{\mathbf{i}}_s+{\mathbf{i}}_s^T\frac{d{\mathbf{L}}_{sr}({\theta }_r)}{d{\theta }_r}{\mathbf{i}}_r\right)\\ & =0.5n_p{\mathbf{i}}_{r\alpha \beta }^T\left(T(-{\theta }_r{)}^T(T_{32}^{-1}{)}^T\frac{d{\mathbf{L}}_{rs}({\theta }_r)}{d{\theta }_r}{T}_{32}^{-1}\right){\mathbf{i}}_{s\alpha \beta }\\ & +0.5n_p{\mathbf{i}}_{s\alpha \beta }^T\left((T_{32}^{-1}{)}^T\frac{d{\mathbf{L}}_{rs}({\theta }_r)}{d{\theta }_r}{T}_{32}^{-1}T(-{\theta }_r)\right){\mathbf{i}}_{r\alpha \beta }\end{array}$$
化简得到：
$$T_e=1.5n_p{L}_M(i_{r\alpha }{i}_{s\beta }-i_{r\beta }{i}_{s\alpha }),(L_M=1.5L_m)$$

其中，用到了：
$$\begin{array}{rl}{\mathbf{i}}_s& =T_{32}^{-1}{\mathbf{i}}_{s\alpha \beta }\\ {\mathbf{i}}_r& =T_{32}^{-1}T(-{\theta }_r){\mathbf{i}}_{r\alpha \beta }\\ {\mathbf{i}}_r^T& ={\mathbf{i}}_{r\alpha \beta }^{T}T(-{\theta }_r{)}^T(T_{32}^{-1}{)}^T\end{array}$$

计算过程：

再把定子转子的磁链方程代入，转矩方程也可以用磁链来表示（把电流全部用磁链表示），如下：

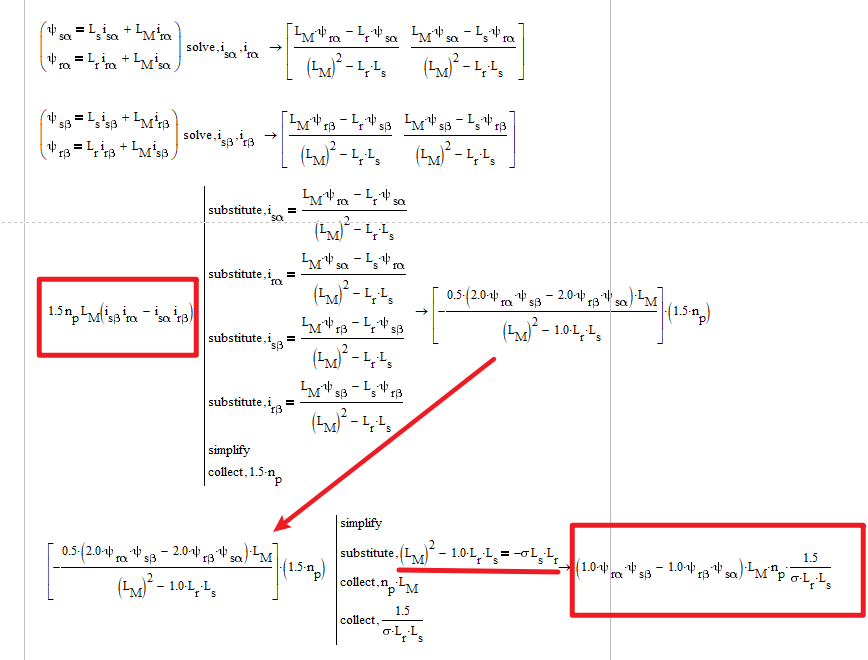
类似地，也可以使用磁链和电流的乘积表示。因此，转矩可以在4个物理量中选择2个来表示：

1. 定子电流
2. 定子磁链
3. 转子电流
4. 转子磁链

所有6种形式的转矩表达式：

$$\begin{array}{rl}{T}_e& =1.5n_p{L}_M(i_{s\beta }{i}_{r\alpha }-i_{s\alpha }{i}_{r\beta })\\ & =1.5n_p({\psi }_{s\alpha }{i}_{s\beta }-{\psi }_{s\beta }{i}_{s\alpha })\\ & =1.5n_p({\psi }_{r\beta }{i}_{r\alpha }-{\psi }_{r\alpha }{i}_{r\beta })\\ & =\frac{1.5n_p{L}_M}{L_r}({\psi }_{r\alpha }{i}_{s\beta }-{\psi }_{r\beta }{i}_{s\alpha })\\ & =\frac{1.5n_p{L}_M}{L_s}({\psi }_{s\beta }{i}_{r\alpha }-{\psi }_{s\alpha }{i}_{r\beta })\\ & =\frac{1.5n_p{L}_M}{\sigma L_r{L}_s}({\psi }_{r\alpha }{\psi }_{s\beta }-{\psi }_{r\beta }{\psi }_{s\alpha }),(\sigma =1-\frac{L_M^2}{L_s{L}_r})\end{array}$$

dq坐标系

dq坐标系只做了旋转，幅值不变，因此转矩方程的形式与定子αβ静止坐标系相同。按照之前约定的坐标轴关系，只是把α改为d，β改为q。例如，
$$\begin{array}{rl}{T}_e& =1.5n_p{L}_M(i_{sq}{i}_{rd}-i_{sd}{i}_{rq})\end{array}$$