LeetCode 1105. Filling Bookcase Shelves【记忆化搜索,动态规划】中等

news2024/9/28 15:28:17

本文属于「征服LeetCode」系列文章之一，这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁，本系列将至少持续到刷完所有无锁题之日为止；由于LeetCode还在不断地创建新题，本系列的终止日期可能是永远。在这一系列刷题文章中，我不仅会讲解多种解题思路及其优化，还会用多种编程语言实现题解，涉及到通用解法时更将归纳总结出相应的算法模板。

为了方便在PC上运行调试、分享代码文件，我还建立了相关的仓库：https://github.com/memcpy0/LeetCode-Conquest。在这一仓库中，你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等，还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解，还可以一同分享给他人。

由于本系列文章的内容随时可能发生更新变动，欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。

给定一个数组 books ，其中 books[i] = [thicknessi, heighti] 表示第 i 本书的厚度和高度。你也会得到一个整数 shelfWidth 。

按顺序 将这些书摆放到总宽度为 shelfWidth 的书架上。

先选几本书放在书架上（它们的厚度之和小于等于书架的宽度 shelfWidth ），然后再建一层书架。重复这个过程，直到把所有的书都放在书架上。

需要注意的是，在上述过程的每个步骤中，摆放书的顺序与你整理好的顺序相同。

例如，如果这里有 5 本书，那么可能的一种摆放情况是：第一和第二本书放在第一层书架上，第三本书放在第二层书架上，第四和第五本书放在最后一层书架上。

每一层所摆放的书的最大高度就是这一层书架的层高，书架整体的高度为各层高之和。以这种方式布置书架，返回书架整体可能的最小高度。

示例 1：

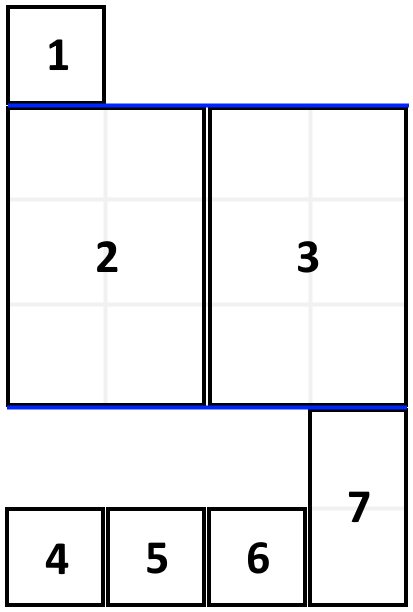
输入：books = [[1,1],[2,3],[2,3],[1,1],[1,1],[1,1],[1,2]], shelfWidth = 4
输出：6
解释：
3 层书架的高度和为 1 + 3 + 2 = 6 。
第 2 本书不必放在第一层书架上。

示例 2:

输入: books = [[1,3],[2,4],[3,2]], shelfWidth = 6
输出: 4

提示：

1 <= books.length <= 1000
1 <= thicknessi <= shelfWidth <= 1000
1 <= heighti <= 1000

解法1 记忆化搜索

对于 books = [[1,1],[2,3],[2,3],[1,1],[1,1],[1,1],[1,2]], shelfWidth = 4 ，第一层放的书可以是 [[1,1] 、或者 [[1,1],[2,3]] ，只要这层书的厚度不超过 shelfWidth 即可。

去掉这段放置完成的书，例如去掉 [[1,1],[2,3]] 后，剩下要解决的问题就是「求出放置 books = [[2,3],[1,1],[1,1],[1,1],[1,2]], shelfWidth = 4 所需的书架最小高度」。这是一个和原问题相似的子问题，所以可以用递归解决。

根据上面的讨论，递归参数只需要一个 i ，dfs(i) 表示放置 books[i:n-1] 这些书所需的书架最小高度。假设这一层放置的最后一本书在 books 中的下标是 j（总体厚度不能超过 shelfWidth ），那么这一层书架的高度为 $\max_{k=i}^{j} \bigg\{ books[k][1]\bigg\}$
考虑「这一层放置的最后一本书」的不同下标 $j$ ，这层书架的高度也不同，而书架总体的最小高度即为「这层书架的高度 + $df s (j + 1)$ 」的最小值，即：
$\min \Bigg\{ \max_{k=i}^{j} \bigg\{ books[k][1]\bigg\} + dfs(j + 1)\Bigg\}$

递归边界： $df s (n) = 0$ 。此时不用放置任何书，书架高度为 $0$ 。
递归入口： $df s (0)$ ，就是答案。

当然，整个递归中有大量重复递归调用（递归入参相同），由于递归函数没有副作用，同样的入参无论计算多少次，算出来的结果都是一样的，因此可以用记忆化搜索来优化。

class Solution {
public:
    int minHeightShelves(vector<vector<int>>& books, int shelfWidth) { 
        int n = books.size(), dp[1010];
        int inf = 0x3f3f3f3f;
        memset(dp, 0x3f, sizeof(dp));
        function<int(int)> dfs = [&](int i) -> int { // 从i开始顺序摆放书,得到的最小书架高度
            if (i >= n) return 0; // 没有书
            if (dp[i] != inf) return dp[i]; // 已有记录
            int sumw = 0, th = 0;
            for (int j = i; j < n; ++j) {
                sumw += books[j][0]; // 厚度
                if (sumw > shelfWidth) break;
                th = max(th, books[j][1]); // 高度 // 可以放在同层
                dp[i] = min(dp[i], th + dfs(j + 1));
            }
            return dp[i];
        };
        return dfs(0);
    }
};

解法2 动态规划

将上述记忆化搜索写成递推形式即可：

class Solution {
public:
    int minHeightShelves(vector<vector<int>>& books, int shelfWidth) { 
        int n = books.size(), dp[1010];
        int inf = 0x3f3f3f3f;
        memset(dp, 0x3f, sizeof(dp));
        dp[n] = 0;
        for (int i = n - 1; i >= 0; --i) {
            int sumw = 0, th = 0;
            for (int j = i; j < n; ++j) { 
                sumw += books[j][0]; // 厚度
                if (sumw > shelfWidth) break;
                th = max(th, books[j][1]); // 高度 // 可以放在同层
                dp[i] = min(dp[i], th + dp[j + 1]);
            }
        }
        return dp[0];
    }
};