1.52N皇后II

参考：代码随想录，52N皇后II；力扣题目链接

1.1.题目

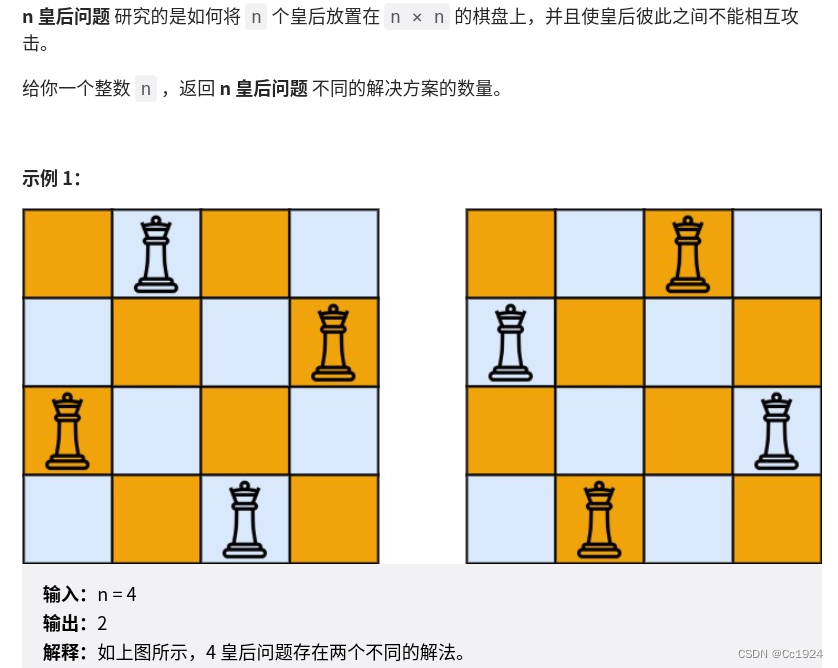
在这里插入图片描述

1.2.解答

这道题和之前做过的 51.N皇后 是一模一样的，只不过51那道题是求所有的棋盘摆放的方案，而本题只需要知道所有的方案的个数。其实只是在统计结果的时候操作不同而已，其他都是一样的。

直接给出代码如下，和51题基本上是一样的。

int count;   // 最后的结果

bool isValid(int row, int col, int n, vector<string>& chess)
{
    // 判断列是否合法
    for(int i = 0; i < row; i++)
        if(chess[i][col] == 'Q')
            return false;
    // 判断左上是否合法
    for(int i = row-1, j=col-1; i >=0 && j>=0; i--, j--)
        if(chess[i][j] == 'Q')
            return false;
    // 判断右上是否合法
    for(int i = row-1, j=col+1; i >=0 && j<n; i--, j++)
        if(chess[i][j] == 'Q')
            return false;
    return true;
}


void backtracking(int row, int n, vector<string>& chess)
{
    // 2.回溯终止条件：放到了最后一行
    if(row == n)
    {
        count++;  // 放满了棋盘格，得到一个合理的解
    }

    // 3.开始递归：遍历这一行的所有列
    for(int col = 0; col < n; col++)
    {
        if(isValid(row, col, n, chess))  // 判断当前位置放一个皇后是否合法
        {
            chess[row][col] = 'Q';   // 放置皇后
            backtracking(row+1, n, chess);   // 递归
            chess[row][col] = '.';   // 回溯
        }
    } 
}

int totalNQueens(int n)
{
    vector<string> chess(n, string(n, '.'));  // 初始化棋盘格
    backtracking(0, n, chess);  // 然后开始遍历，放置皇后
    return count;   // 最后返回所有可能的结果
}

2.649Dota2 参议院

参考：代码随想录，649Dota2 参议院；力扣题目链接

2.1.题目

在这里插入图片描述

2.2.解答

TODO：暂时没有AC，看了代码随想录上的讲解，感觉还挺简单的，但是自己稍微换了一种写法就无法AC了，自己的写法如下：

感觉还是不太明白，因为当前的位置的R和T，都是要优先消灭后面的R和T，这样该怎么操作。

string predictPartyVictory(string senate)
{
    bool haveR = true;
    bool haveT = true;
    int numR = 0;   // 当前位置之前（包括当前位置）含有的R的个数
    int numT = 0;   // 当前位置之前（包括当前位置）含有的T的个数

    // 只要数组中还有R并且还有T，那么就还没有消灭完毕，则继续消灭
    while(haveR && haveT)
    {
        // 先认为没有R和T了，如果后面执行过程中被修改成true了，则说明还有R和T
        haveR = false;
        haveT = false;  
        for(int i = 0; i < senate.size(); i++)
        {
            if(senate[i] == 'R')
            {
                numR++;   // 首先字符R的个数++
                if(numT >= numR)   // 如果当前位置前面的T个数 >= 当前位置R的个数，则可以消灭
                {
                    senate[i] = 0;  // 消灭R，为下一次循环做准备
                    numR--;
                }
                else
                    haveR = true;   // 否则不能消灭R，置位
            }
            else if(senate[i] == 'T')
            {
                numT++;
                if(numR >= numT)
                {
                    senate[i] = 0;
                    numT--;
                }
                else
                    haveT = true;
            }
        }
    }

    return haveR == true ? "Radiant" : "Dire";  // 根据最后haveR还是T返回结果
}

3.1221分割平衡字符串

参考：代码随想录，1221分割平衡字符串；力扣题目链接

3.1.题目

在这里插入图片描述

3.2.解答

这道题目看起来好像很复杂，其实是非常简单的贪心。

从前向后遍历，只要遇到平衡子串，计数就+1，遍历一遍即可。

局部最优：从前向后遍历，只要遇到平衡子串就统计

全局最优：统计了最多的平衡子串。

局部最优可以推出全局最优，举不出反例，那么就试试贪心。

例如，LRLR 这本身就是平衡子串 , 但要遇到LR就可以分割。

最后直接给出代码如下，非常简单：

int balancedStringSplit(string s)
{
    int result = 0; // 最后平衡字符串的个数
    int count = 0;  // 字符串中R的个数

    // 遍历一遍字符串，寻找平衡子串
    for (const auto &ch : s)
    {
        if (ch == 'R')
            count++;
        else
            count--;
        if(count == 0)  // 遇到一个平衡子串
            result++;
    }
    
    return result;
}