目录
1 几何建模简介
1.1 机器人建模
1.2 环境建模
2 多边形和多面体模型
2.1 凸集的定义
2.2 凸集的边界表示与实心表示
2.3 非凸多边形
2.4 逻辑谓词
2.5 多面体模型
2.6 阿拉伯数字半代数模型
2.7 非凸多边形的另一种编码
2.8 3D三角形
2.9 非均匀有理B样条曲线
2.10 位图
2.11 更广义的定义
本文对机器人运动规划的经典书籍《planning algorithm》进行解析,原文请参考3.1 Geometric Modeling (lavalle.pl)
1 几何建模简介
对于运动规划,如何对机器人和环境进行几何建模是非常重要的内容。几何建模的方法和技术多种多样,具体的选择通常取决于应用和问题的难度。在大多数情况下,通常有两种选择:边界表示与实心表示。
1.1 机器人建模
假设我们想要定义一个机器人的模型。利用边界表示法,可以写出与机器人表面大致重合的方程。若用实心表示,我们可以描述机器人实体中包含的所有点的集合。
1.2 环境建模
第一步是定义世界W,有两种可能的选择:(1)2D世界,其中W = R2, (2) 3D世界,其中W = R3。这样的定义足以解决大多数问题,然而,人们也可能希望允许更复杂的世界如更高维度的空间,本篇文章不讨论这些,因为它们目前的应用是有限的。第二步是定义障碍物区域:世界中“永久”被占领的部分,例如建筑的墙壁。
2 多边形和多面体模型
2.1 凸集的定义
首先介绍凸集,当且仅当,对于X中的任何一对点,连接它们的线段上的所有点都包含在X中。因此,x1和x2之间的插值总是在X中产生点。直观地说,X不包含口袋或缩进。
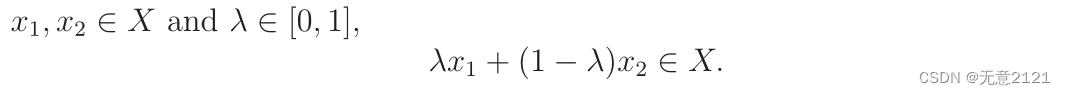
2.2 凸集的边界表示与实心表示
O的边界表示是一个m边多边形,它可以用两种特征来描述:顶点和边。每个顶点对应多边形的一个“角”,每个边对应一对顶点之间的线段。多边形可以用R2中m个点的序列(x1, y1), (x2, y2),…,(xm, ym)来表示,按逆时针顺序给出。
O的实心表示可以表示为m个半平面的交。每一个半平面对应于多边形边所共有的直线一侧的所有点的集合。下图显示了一个八边形的例子,它表示为八个半平面的交点。
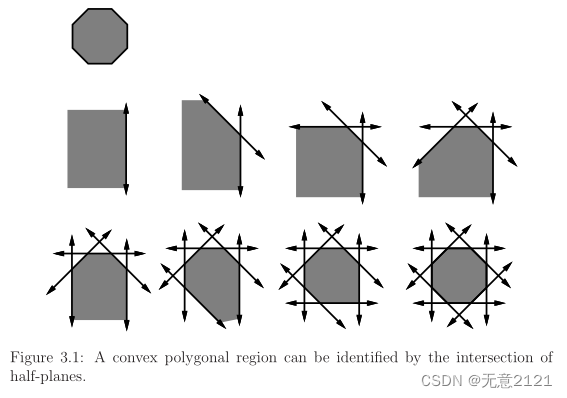
多边形的边由两点指定,例如(x1, y1)和(x2, y2)。考虑经过(x1, y1)和(x2, y2)的直线方程。可以确定一个方程的形式为ax + by + c = 0,其中a, b, c∈R是由x1, y1, x2, y2确定的常数。设f: R2→R为f(x, y) = ax + by + c给出的函数,注意直线的一边是f(x, y) < 0,另一边是f(x, y) > 0。事实上,f可以解释为(x, y)到直线的有符号欧氏距离,f(x, y)的符号表示以该线为界的半平面,设fi(x, y)表示从(xi, yi)到(xi+1, yi+1)边对应的直线f函数。

Hi对于1≤i≤m定义为W的一个子集。Hi是描述直线fi(x, y) = 0(包括直线上的点)一侧所有点的集合。
![]()
凸的m边多边形障碍区域可以是多个半空间的交集,因此O表示为
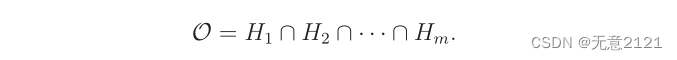
2.3 非凸多边形
但O作为多边形障碍区域是凸边形的假设太有限。现在假设O是w的一个非凸多边形。在这种情况下,O可以表示为
![]()
其中每个Oi都是一个凸多边形集。使用这种表示,可以定义W中非常复杂的障碍区域。尽管这些区域可能包含多个分量和孔洞,但只要O是有界的,它的边界将由线性段组成。因此,O可以定义为任何有限的并集、交集和差集的组合。
注意,非凸多边形的表示不是唯一的。有很多方法可以将O分解为凸集(经典的三角剖分)。应该仔细选择分解,以优化将使用该模型的任何算法的计算性能。在大多数情况下,组件甚至可能被允许重叠。理想情况下,用最少数量的基元表示O似乎很好,但是自动化这样的分解可能会导致NP-hard问题。分解O的一种高效、实用的方法是应用垂直单元格分解算法
2.4 逻辑谓词
我们可以先定义一个逻辑谓词作为碰撞检测器。设φ是一个谓词,定义为φ: W→{true, false},如果W中的点位于O,则返回true,否则返回false。对于f(x, y) = 0给出的直线,设e(x, y)表示一个逻辑谓词,如果f(x, y)≤0则返回true,否则返回false。与凸多边形区域相对应的谓词用逻辑连接表示
![]()
如果点(x, y)位于凸多边形区域,谓词α(x, y)返回真值,否则返回假值。则由n个凸多边形组成的障碍区域用并集的逻辑表示
![]()
虽然存在更有效的方法,但φ可以在时间O(n)检查点(x, y)中是否位于O,其中n是O表示中出现的集合的数量。
2.5 多面体模型
对于三维世界,W = R3,前面的概念可以很好地从二维的情况下推广,用多面体代替多边形,用半空间代替半平面。边界表示可以根据三个特征定义:顶点、边和面。每个面都是一个嵌入R3中的“平面”多边形。每条边都构成了两个面之间的边界。每个顶点形成三条或多条边之间的边界。
已经提出了几种数据结构,允许人们方便地绕着多面体特征“走”。例如,双连接边缘列表。数据结构包含三种类型的记录:面、半边和顶点。直观地说,半边是有向边。每个顶点记录保存着点坐标和指向与顶点接触的任意半边的指针。每个面记录都包含一个指向其边界上任意半边的指针。每个面都由半边组成的圆形列表限定。多面体的每条边都有一对有向半边记录。每条半边如图3.3b中的箭头所示。每个半边记录包含指向其他5个记录的指针:1)半边起源于顶点;2)“孪生”半边,限定相邻面,且方向相反;3)以半边为界的面;4)绑定面的圆形边列表中的下一个元素;和5)前一个元素的圆形列表边绑定的脸。一旦定义了所有这些记录,就可以方便地遍历多面体的结构。更多关于该数据结构的介绍请参考lect10-dcel.pdf (umd.edu)
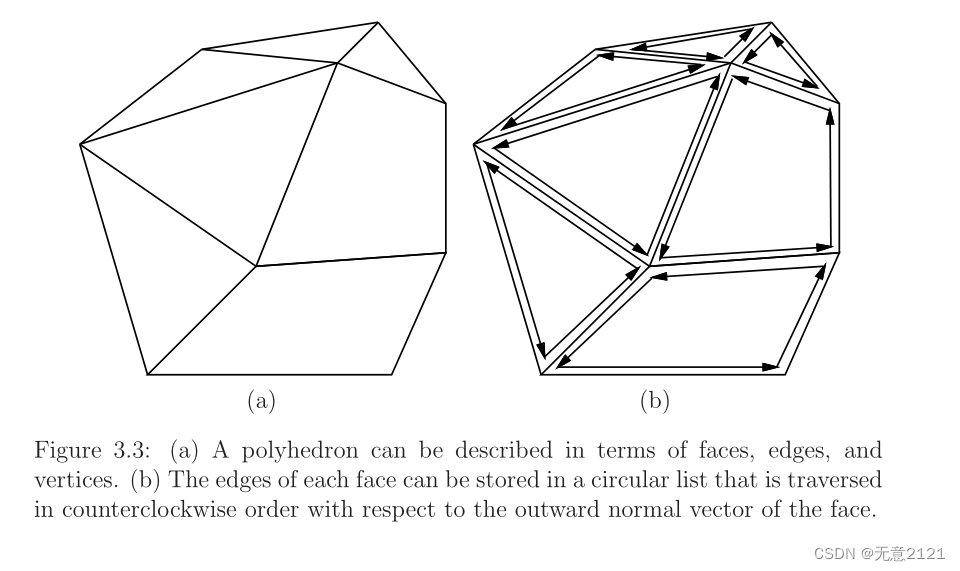
现在考虑一个多面体的实心表示。假设O为凸多面体,可以从顶点构造一个实体表示。O的每个面沿其边界至少有三个顶点。假设这些顶点不共线,通过它们的平面的方程可以确定为
![]()
同样可以构造f,除了f: R3→R和f(x, y, z) = ax + by + cz + d。设m为面数。对于O的每一个面,定义一个半空间Hi为W的子集
![]()
2.6 阿拉伯数字半代数模型
在多边形和多面体模型中,f 都是线性的。在二维世界的半代数模型的情况下,可以是具有实值系数和变量的任何多项式。构造的方式与上面的交集并集类似。
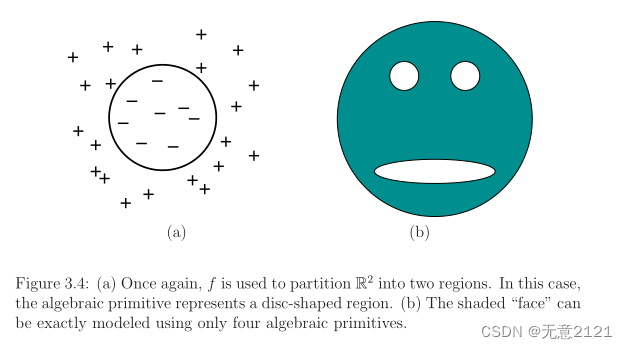
2.7 非凸多边形的另一种编码
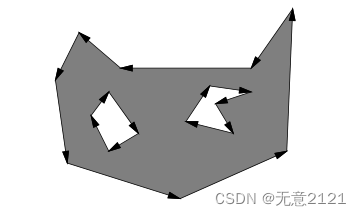
上述方法需要非凸多边形表示为凸多边形的并集。现在提出一种新的方法,可以表示带孔的多边形。 通过使用不同的方向:逆时针为外部边界和顺时针为孔边界。
2.8 3D三角形
最方便的几何模型之一是一组三角形,每个三角形由三个点表示,这在计算机图形学中很流行,因为图形加速硬件主要使用三角形基元。若两个三角形如果有交集,则被视为“碰撞” 另一个。允许三角形基元有交集提供了极大的灵活性,因为没有对三角形表达方式的限制,这产生了表达的多解,然而这也是缺点之一。没有连贯性可以求出一个三角形顶点是否在另一个三角形“内部”来判断。如果至少有一些连贯性, 那么有时最好减少冗余三角形坐标的规范(许多三角形将共享相同的点或边)。删除此冗余的表示称为三角形条带,它是一系列三角形,使得每个相邻的三角形共享一个共同的边。一个三角形扇形,其中所有三角形共享一个共同的顶点。
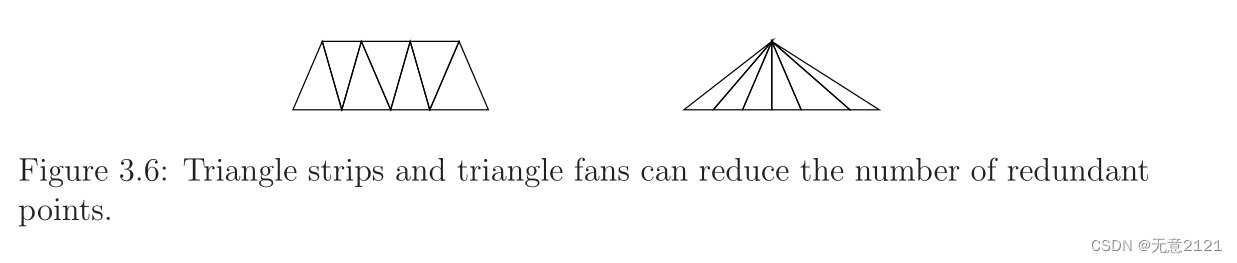
2.9 非均匀有理B样条曲线
非均匀有理B样条曲线用于许多工程设计系统,以方便曲面的设计和调整,如飞机或汽车车身设计。半代数是隐式方程,而NURBS 和其他样条曲线是参数方程。这使得诸如渲染之类的计算容易;但是,其他功能(例如碰撞检测)变得更加多难。这些模型可以在任何维度上定义。这里给出了 2D 公式,更多B样条曲线细节可以阅读《考虑车辆运动约束的最优避障轨迹规划算法》论文解读二_无意2121的博客-CSDN博客
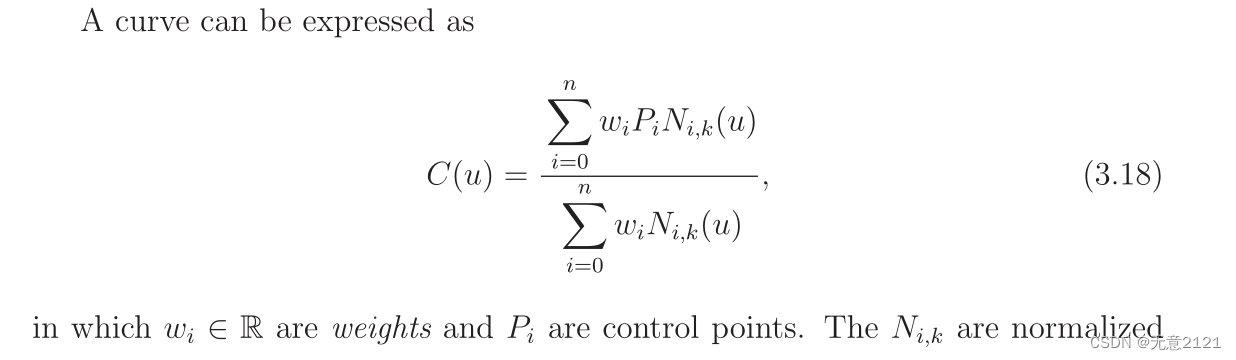
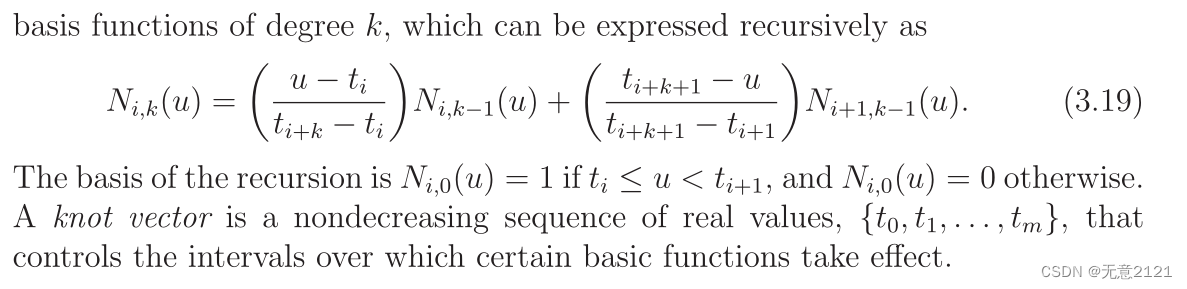
2.10 位图
对于W = R2或W = R3,都可以将世界的有界部分离散成可能被占用或不被占用的矩形单元格。这种离散化的分辨率决定了每个轴的单元格数量和大小。这种表示可以被认为是一个二值图像,其中图像中的每个“1”对应一个包含至少一个O点的矩形区域,而“0”表示不包含任何O点的区域。尽管位图不像其他模型那样优雅,但它们在应用中经常出现。其中一个例子是由移动机器人通过传感器探索环境而构建的数字地图。位图的一个概括是灰度图或占用网格。在这种情况下,可以为每个单元格分配一个数值,表示诸如“存在障碍的概率”或“穿越单元格的预期难度”等数量。后一种解释常用于为行星漫游车导航的地形图中。更多详细的建图内容可以参考【自动驾驶轨迹规划之地图结构】_无意2121的博客-CSDN博客
2.11 更广义的定义
不仅可以用多项式来定义f ,一个流行的基元是超二次元,它概括了二次曲面。一个例子是超椭球体
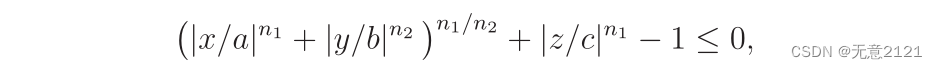
广义圆柱是普通圆柱的推广。对于某些参数s∈[0,1],中轴不是局限于一条直线,而是一条连续的脊柱曲线(x(s), y(s), z(s))。沿着脊柱定义了一个半径函数r(s),而不是一个恒定的半径。r(s)的值是作为广义圆柱在点(x(s), y(s), z(s)的截面得到的圆的半径。横截面平面的法线是脊柱曲线在s处的切线。