堆是什么?
是土堆吗?

那当然不是啦~
堆是一种被看作完全二叉树的数组。
那么什么是完全二叉树呢?
如果二叉树中除去最后一层节点为满二叉树,且最后一层的结点依次从左到右分布,则此二叉树被称为完全二叉树。
堆的特点:对于这个树的任意节点来说,满足根节点大于左右子树的值(大堆),或者任意一节点满足根节点的值小于左右子树的值(小堆)
那么来看一下堆是如何?
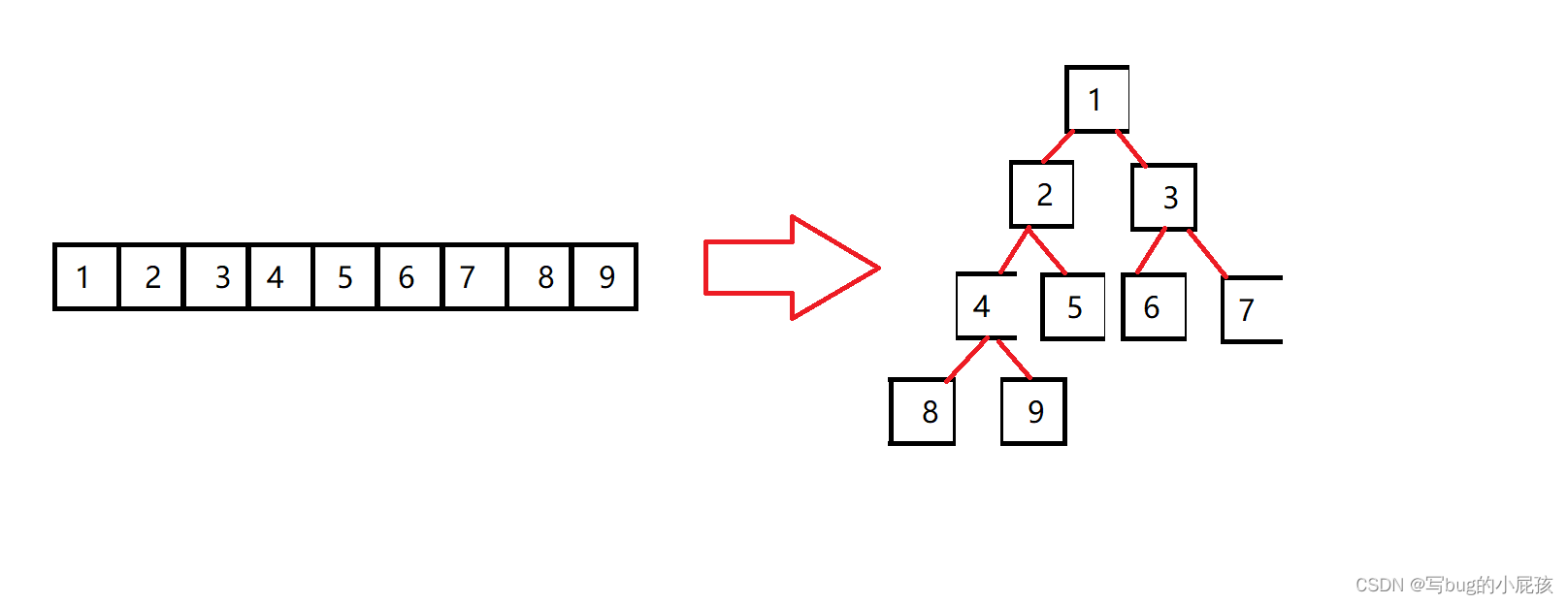
是不是很好理解?其实本质就是一个装着数据的数组,但我们将它想象成一个树,
一棵完全二叉树。
而且这棵二叉树是一个小根堆,即父亲小于或等于它的左子树和右子树的值
那么我们就来实现这个堆的基本操作吧
堆的基本操作
1.定义堆的结构体
typedef int HPDataType;
typedef struct Heap
{
HPDataType* data;
int size;//堆当前的有效元素个数
int capacity;//堆的容量
}Heap;由于堆是一个数组,所以我们需要用顺序表的形式动态的管理它。所以在这个结构体里头我们定义了该结构体数据类型的数组用来存储数据,size用于展示当前堆的有效元素个数,capacity用于展示当前堆的容量。
2.堆的初始化
Heap* HeapInit()
{
Heap* hp = (Heap*)malloc(sizeof(Heap));
if (hp == NULL)
{
perror("malloc fail");
return;
}
HPDataType* data = (HPDataType*)malloc(sizeof(HPDataType) * 2);
if (data == NULL)
{
perror("malloc fail");
return;
}
hp->data = data;
hp->capacity = 2;
hp->size = 0;
return hp;
}在堆区建立一个堆的结构体,让里面的数组大小设置为2(纯属个人习惯),两次malloc可能都会弄成NULL,所以一定要记得用if检查一下,之后perror一下malloc的错误,如果创建成功,那么将该结构体的数据依次设置完毕,返回该结构体的指针。
3.堆的销毁
void HeapDestory(Heap* hp)
{
assert(hp);
free(hp->data);
hp->capacity = 0;
hp->size = 0;
free(hp);
hp = NULL;
}这个还是比较简单的,只需要先将堆的结构体里面的data释放,再将该结构体释放即可,当然两个顺序千万别反过来。free了之后记得养成好习惯将指针都置为NULL
4.堆的向下调整
这是堆的基本操作中最重要的操作之一,那么我们先来看一下向下调整的相关规则:
ex:以小根堆为例
1.先设置当前结点为根结点,之后通过根节点找到左右子树结点,之后比较左右子树的值,通过比较两个值,选出的那个数值较小的值的结点作为child。
2.再比较根结点(父母结点)和那个数值较小的child结点的值,如果child的结点比parent的结点的值更小,那么两个结点进行交换。
3.如果child结点比parent结点的值更大,那么已符合小根堆的规则,那么我们就会调整结束。
4.处理完这个结点后,如果符合第2条规律,就继续以该child结点进行循环操作,直到出现child < n或者符合第3条规则。
那么就来看我们的代码叭~
void AdjustDown(HPDataType* data, int n, int parent)
{
int child = parent * 2 + 1;
while (child < n)
{
//找出最小/大的那个孩子,先默认最小/大为左孩子,而且,child+1小于n
if (child + 1 < n && data[child] > data[child + 1])
{
child++;
}
if (data[child] < data[parent])
{
Swap(&data[child], &data[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}可能有人发现了,为什么我的左右孩子节点能够通过parent * 2 + 1或parent * 2 + 2获得,那是因为堆是一棵完全二叉树,又因为根节点初始的下标是0,那么通过对该特点的分析,我们就可以得出:
1.childleft = parent * 2 + 1, childright = parent * 2 + 2;
2.parent = (child - 1) / 2
5.堆的向上调整
我们还是来看堆的向上调整的相关规则:
1.先设置当前结点为孩子结点,通过上述的相关结论,我们通过孩子找到了它的父母结点。
2.比较父母结点的值和孩子结点的值,如果孩子结点的值比较小,那么我们就交换两个结点。
3.如果孩子结点的值比较大,那么我们就调整结束
4.如果符合第2条规则,我们会将parent作为新的孩子继续循环,直到child > 0或者符合第3条规则
void AdjustUp(HPDataType* data, int child)
{
int parent = (child - 1) / 2;
while (child > 0)
{
//我默认为小根堆
if (data[child] < data[parent])
{
Swap(&data[child], &data[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}6.获取堆顶元素的值
直接来看代码:
HPDataType HeapTop(HP* php)
{
assert(php);
return (php->data[0]);
}这就没什么好说的了,数组嘛,直接下标访问即可
7.判断堆是否为空
bool HeapEmpty(HP* php)
{
assert(php);
return (php->size) == 0;
}只需要判断这个堆的有效元素个数是否为0即可
8.堆的有效元素个数
int HeapSize(HP* php)
{
assert(php);
return php->size;
}9.入堆操作
展示代码之前,先提几个问题:
1.一个元素从堆这个数组的尾部直接入堆,这个数组是否还是一个大根堆或一个小根堆呢?
很显然,这并不一定是一个大根堆或小根堆。
2.那么如果从堆的头部入堆,是否能是一个大根堆或是一个小根堆呢?
很显然,这比第一点还要离谱一些,不仅仅只是大根堆和小根堆的问题了,如果从头部头插入堆,首先就是移动后面的数据就很麻烦,如果数据量大,那要移动到猴年马月?而且,如果头插入堆,会直接把堆原本的父子结构给破坏了,那这样就得不偿失了。
所以我们一定是只能先从尾部进行入堆之后再进行其他的操作,让整个数组重新变成一个堆。
那么我们怎么才能让这个数组重新变成一个堆呢?
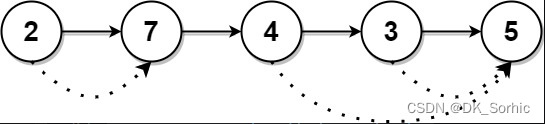
我们来看一下下面的一组图:
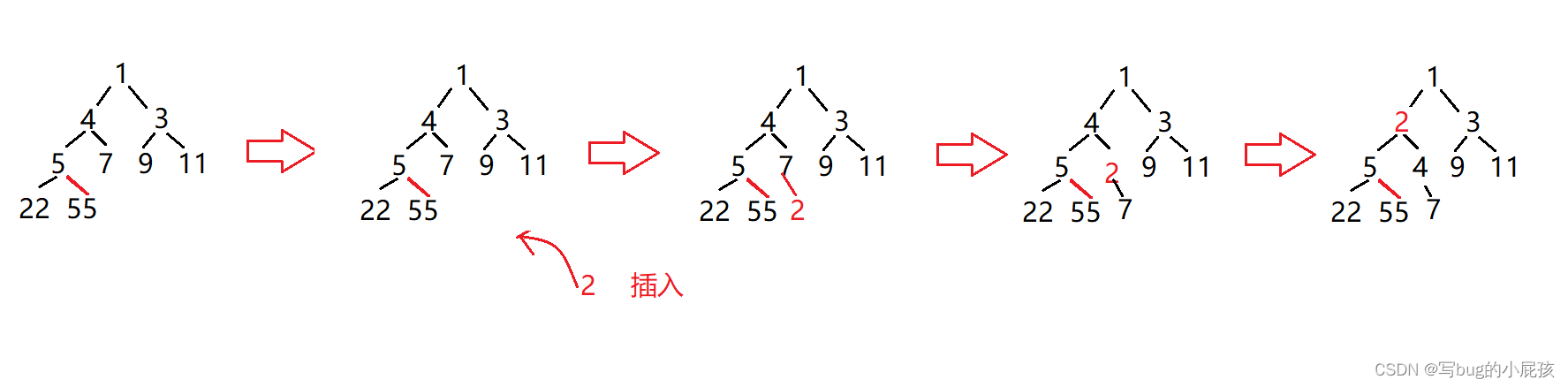
我们通过这个图也就可以得出插入数据的完整过程了
1.先将想要入堆的数据插入整个数组的最尾部
2.之后通过向上调整,将该数据调整到合适的位置即可,这就完成了堆的插入数据,这样还能让这个数组保持堆的性质,不会破坏整个堆的父子关系结构。
那么就来看代码叭!
void HeapPush(HP* php, HPDataType x)
{
assert(php);
//push之前判断堆满了没
if (php->capacity == php->size)
{
HPDataType* tmp = (HPDataType*)realloc(php->data, sizeof(HPDataType) * php->capacity * 2);
if (tmp == NULL)
{
perror("realloc fail");
return;
}
php->capacity = php->capacity * 2;
php->data = tmp;
}
php->data[php->size] = x;
(php->size)++;
AdjustUp(php->data, php->size - 1);
}当然啊,一定要判断这个堆是否满了,满了一定要先realloc一下这个数组,让我们的数组能够正常地存入数组当中,将数组的有效元素个数自增1。
10.出堆顶数据操作
还是先来问一个问题,直接让数组的第一个元素出堆能不能直接解决问题?
是的,不能,我们不能直接删除,如果删了之后,我们需要一个个元素移动,而且我们上面已经提到过了,如果移动整个数组,会影响我们的堆的父子关系的结构,所以我们不能直接删除。
那么我们应该如何删除呢?
来看下面的图:
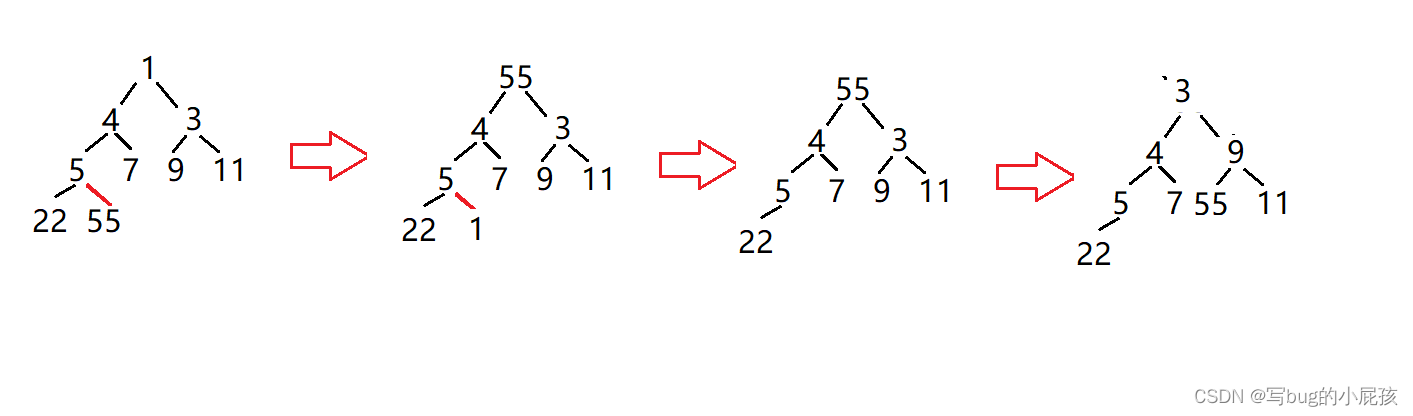
这图直接就能让我有了思路:
1.先将数组的首元素和数组的尾元素调换位置
2.之后将size--,我们就可以直接删除这个元素了。
3.我们再让堆顶的元素向下调整,就能让我们的数组重新变成一个堆。
嗯,完美!
直接来看代码叭!
void HeapPop(HP* php)
{
assert(php);
//删除数据的时候要判断堆是否为空
assert(!HeapEmpty(php));
Swap(&(php->data[0]), &(php->data[php->size - 1]));
(php->size)--;
AdjustDown(php->data, php->size, 0);
}当然,还是要判断我们的堆是否为空,空了的话,我们就删了个寂寞了。
那么,这就是整个堆了啦!
那么堆排序到后面的排序算法的时候再将,拜拜~