2016-2017 ACM-ICPC Nordic Collegiate Programming Contest (NCPC 2016)
A - Artwork
题目描述:
给定N*M的网格,给出Q次询问,每次询问都给出一个小矩阵,保证每个矩阵要么长为1,要么宽为1,将网格中矩阵部分涂黑,每次询问都要回答到目前为止白色部分的联通块的数量
思路:
很经典的一种离线考察方法,先将所有询问保存下来,离线并查集处理
从后往前去取消覆盖,来获得答案
开一个二维数组记录网格被涂黑的次数,当次数变成0以后,就把它与上下左右四个方向进行合并,并更新联通块的数量
很简单的思路,不过写起来有点恶心
#include<bits/stdc++.h>
using namespace std;
#define m_p(a, b) make_pair(a, b)
#define endl '\n'
#define io ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)
#define pb push_back
typedef long long ll;
typedef pair<int, int> pii;
#define MAX 1000050
#define y1 y114514
#define lowbit(x) (x&(-x))
int x, y, z, n, m, k;
int num[1005][1005];
struct ran{
int x1, y1, x2, y2;
}tr[MAX];
int fa[1500005];
int getfa(int x){
return fa[x] == x ? x : fa[x] = getfa(fa[x]);
}
int getid(int x, int y){
return (x-1)*m + y;
}
bool judge(int x, int y){
if(x > n || x < 1 || y > m || y < 1)return false;
if(num[x][y])return false;
return true;
}
int dx[] = {1, 0, -1, 0};
int dy[] = {0, 1, 0, -1};
void emerge(int x, int y){
fa[getfa(x)] = getfa(y);
}
int ar[MAX];
void work(){
cin >> n >> m >> k;
for(int i = 1; i <= 1500000; ++i)fa[i] = i;
for(int i = 1; i <= k; ++i){
cin >> tr[i].x1 >> tr[i].y1 >> tr[i].x2 >> tr[i].y2;
if(tr[i].x1 == tr[i].x2){
for(int j = tr[i].y1; j <= tr[i].y2; ++j)++num[tr[i].x1][j];
}
else for(int j = tr[i].x1; j <= tr[i].x2; ++j)++num[j][tr[i].y1];
}
for(int i = 1; i <= n; ++i){
for(int j = 1; j <= m; ++j){
if(num[i][j])continue;
for(int k = 0; k < 4; ++k){
int xx = i + dx[k];
int yy = j + dy[k];
if(judge(xx, yy))emerge(getid(i,j), getid(xx, yy));
}
}
}
set<int>se;
for(int i = 1; i <= n; ++i){
for(int j = 1; j <= m; ++j){
if(!num[i][j]){
se.insert(getfa(getid(i, j)));
}
}
}
int tot = (int)se.size();
ar[k] = tot;
for(int i = k; i > 1; --i){
if(tr[i].x1 == tr[i].x2){
for(int j = tr[i].y1; j <= tr[i].y2; ++j){
--num[tr[i].x1][j];
if(num[tr[i].x1][j] == 0){
set<int>se;
for(int p = 0; p < 4; ++p){
int xx = tr[i].x1 + dx[p];
int yy = j + dy[p];
if(judge(xx, yy)){
se.insert(getfa(getid(xx, yy)));
}
}
tot = tot - se.size() + 1;
int id = getid(tr[i].x1, j);
fa[id] = id;
for(auto x :se)fa[x] = id;
}
}
}
else{
for(int j = tr[i].x1; j <= tr[i].x2; ++j){
--num[j][tr[i].y1];
if(num[j][tr[i].y1] == 0){
set<int>se;
for(int p = 0; p < 4; ++p){
int xx = j + dx[p];
int yy = tr[i].y1 + dy[p];
if(judge(xx, yy)){
se.insert(getfa(getid(xx, yy)));
}
}
tot = tot - se.size() + 1;
int id = getid(j, tr[i].y1);
fa[id] = id;
for(auto x :se)fa[x] = id;
}
}
}
ar[i-1] = tot;
}
for(int i = 1; i <= k; ++i)cout << ar[i] << " ";
cout << endl;
}
int main(){
io;
work();
return 0;
}


C Card Hand Sorting
题目描述:
给出n张有花色有数字的卡片,你每次可以将一张卡片移动到任意一个位置,问最少需要多少次可以将相同花色的卡片放在一起,且保证花色相同的卡片中数字是有序的(无论升序还是降序)
思路:
比赛的时候读假题了,三个人对着假代码思考了半个小时也没找出来哪里有问题,后来发现我读漏条件了,md
首先思考一下,假设给定一个最终状态,从原始状态变成最终状态最少需要多少步该怎么求?我们可以用最长公共子序列来求,由于每次操作只是将一个数字移动到一个新的位置,所以不需要操作的数字的位置是相对不变的,我们跟最终状态求一个最长公共子序列就能求出不需要移动的数字的数量,用长度减去找个数字就能求出最小操作次数
花色的数量只有4种,所以最多枚举4!种花色的排列方式,再此基础上可以再枚举一下每种花色是升序还是降序,也就是24
复杂度是 o ( 4 ! ∗ 2 4 ∗ n 2 ) o(4! * 2^4*n^2) o(4!∗24∗n2)
#include<bits/stdc++.h>
using namespace std;
#define MAX 300050
int n, m;
string cao[100];
map<char, int>bijiao;
char sr[] = {'s', 's', 'h', 'd', 'c'};
int dp[60][60];
int fuck(vector<string> s, vector<string> t){
int len1 = s.size(), len2 = t.size();
memset(dp, 0, sizeof(dp));
for(int i = 1; i <= len1; ++i){
for(int j = 1; j <= len2; ++j){
if(s[i-1] == t[j-1]){
dp[i][j] = dp[i - 1][j - 1] + 1;
}
else dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
}
}
return dp[len1][len2];
}
vector<string> cnm(vector<string> v, bool op){
for(int i = 0; i < v.size(); ++i){
for(int j = i+1; j < v.size(); ++j){
if(bijiao[v[i][0]] > bijiao[v[j][0]]){
swap(v[i], v[j]);
}
}
}
if(op == 1)reverse(v.begin(), v.end());
return v;
}
void work(){
cin >> n;
for(int i = 2; i <= 9; ++i){
bijiao[(char)('0'+i)] = i;
}
bijiao['T'] = 10;
bijiao['J'] = 11;
bijiao['Q'] = 12;
bijiao['K'] = 13;
bijiao['A'] = 14;
char x;
map<char, int>mp;
map<char, vector<string>>mpp;
vector<string>s;
mp['s'] = 1;mp['h'] = 2;mp['d'] = 3;mp['c'] = 4;
for(int i = 1; i <= n; ++i){
cin >> cao[i];
s.push_back(cao[i]);
x = cao[i][1];
mpp[x].push_back(cao[i]);
}
int ar[] = {0, 1, 2, 3, 4};
int ans = 1e9;
do{
for(int i = 0; i < 16; ++i){
vector<string>t;
for(int j = 1; j <= 4; ++j){
vector<string>aa = cnm(mpp[sr[ar[j]]], (i>>(j-1)&1));
for(auto x : aa)t.push_back(x);
}
ans = min(ans, n - fuck(s, t));
}
}while(next_permutation(ar+1, ar+5));
cout << ans << endl;
}
int main(){
work();
return 0;
}
D Daydreaming Stockbroker
题目描述:
给出一支股票在接下来n天内的价格,你的启动资金有100$,你可以在任意的天内买入或者卖出股票,数量任意,但不超过100000股(即你手中最多持有100000股),问在最后一天结束以后,你最多能拥有多少钱
思路:
贪心
如果今天的股票价格大于上一天的,就在i-1天的价格购入能买的最大数量支股票,以第i天的价格全卖出去,更新钱的数量
#include<bits/stdc++.h>
using namespace std;
#define m_p(a, b) make_pair(a, b)
#define endl '\n'
#define io ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)
#define pb push_back
typedef long long ll;
typedef pair<int, int> pii;
#define MAX 1000050
#define y1 y114514
#define lowbit(x) (x&(-x))
ll x, y, z, n, m, k;
ll tr[MAX];
void work(){
cin >> n;
for(int i = 1; i <= n; ++i)cin >> tr[i];
m = 100;
for(int i = 2; i <= n; ++i){
if(tr[i] > tr[i - 1]){
k = min(100000ll, m / tr[i - 1]);
m += k * (tr[i] - tr[i - 1]);
}
}
cout << m << endl;
}
int main(){
io;
work();
return 0;
}
F Fleecing the Raffle
题目描述:
n个球抓k个球的游戏,现在你可以往里放若干个球,使得自己中奖的概率最高,问概率最高是多少
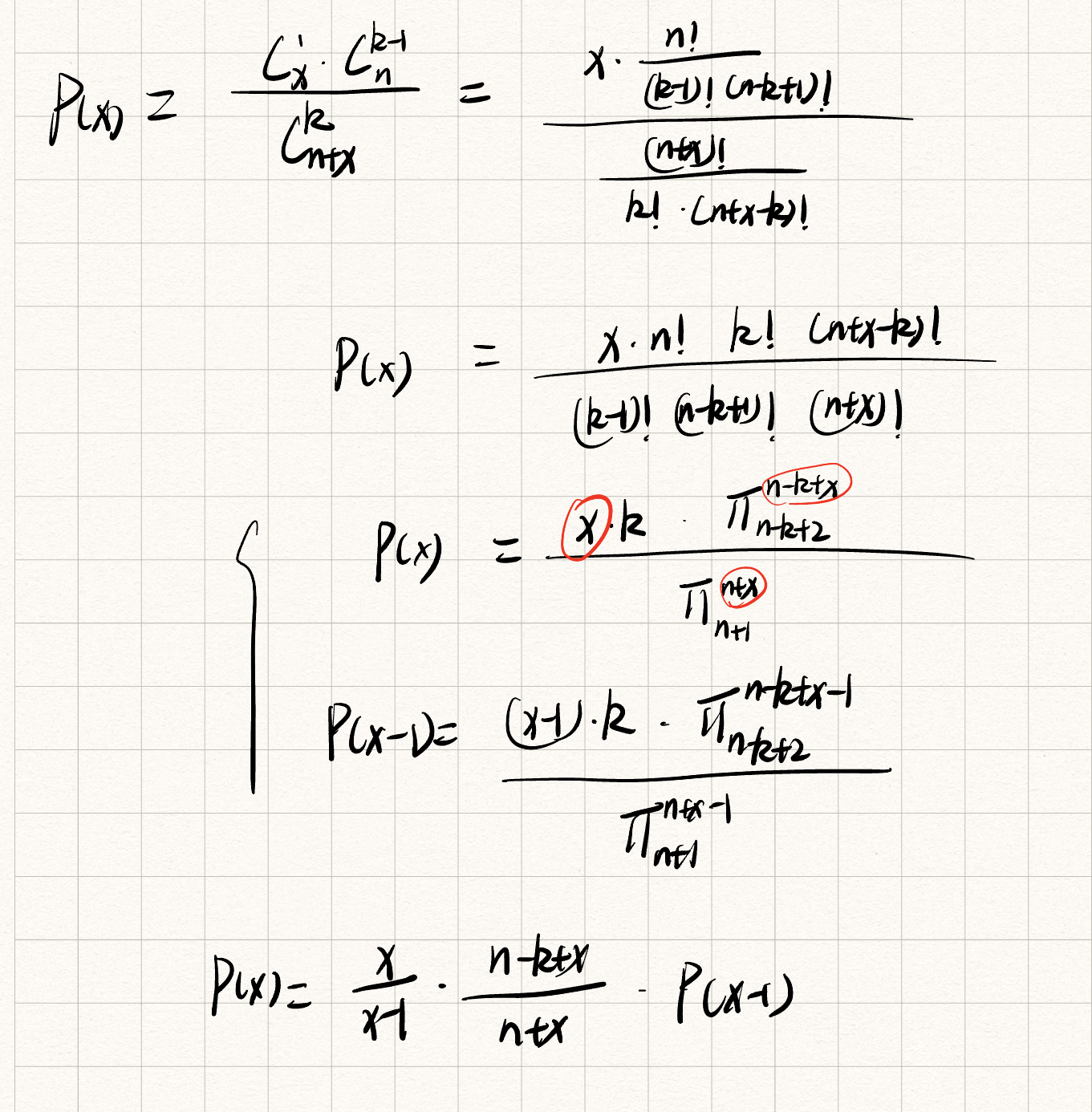
思路:
推公式
#include<bits/stdc++.h>
using namespace std;
#define MAX 300050
double n, p;
void work(){
cin >> n >> p;
double pre = 1.0*p/(n+1);
double now = pre;
for(double i = 2; ;++i){
now = now * i / (i - 1) * (n - p + i) / (n+i);
if(now<pre){
printf("%.10f\n", pre);
return;
}
pre = now;
}
}
int main(){
work();
return 0;
}
G Game Rank
题目描述:
模拟题,懒得复述题意了
#include<bits/stdc++.h>
using namespace std;
#define MAX 300050
int n, m;
int num[MAX] ;
void work(){
string s;cin>>s;
for(int i = 1; i <= 10; ++i)num[i] = 5;
for(int i = 11; i <= 15; ++i)num[i] = 4;
for(int i = 16; i <= 20; ++i)num[i] = 3;
for(int i = 21; i <= 25; ++i)num[i] = 2;
int star = 0;
int grade = 25;
int cont = 0;
for(auto x : s){
if(x == 'W'){
++cont;
++star;
if(cont >= 3 && grade>=6)++star;
if(star > num[grade] ){
star -= num[grade];
--grade;
}
if(grade == 0){
cout << "Legend\n";
return;
}
}
else{
cont = 0;
if(grade > 20 || grade == 0)continue;
if(star){
--star;
}
else{
if(grade == 20)continue;
++grade;
star = num[grade] - 1;
}
}
}
cout << grade <<endl;
}
int main(){
work();
return 0;
}
J Jumbled Compass
题目描述:
给你一个360度的罗盘,给出a和b所在的角度,问指针最少转动多少度可以从a转到b,顺时针是+,逆时针是-
思路:
枚举或者分类讨论一下
#include<bits/stdc++.h>
using namespace std;
void work(){
int n, m;
cin >> n >> m;
m = (m - n + 360) % 360;
int k = m - 360;
if(abs(k) < abs(m))cout << k << endl;
else cout << m << endl;
}
int main(){
work();
return 0;
}
总结
这是和wwy组队的第一场比赛,卡牌题我读漏了个条件,导致我们的思路虽然正确,但是漏了个花色内有序,所以卡了半个小时。而且由于时间限制,比赛只打了3个小时,导致A题一眼题但是没时间写,好像还有一个欧拉降幂的题,等有时间再补了