1. 题目介绍（55. 二叉树的深度）

面试题55：二叉树的深度，一共分为两小题：

题目一：二叉树的深度
题目二：平衡二叉树

2. 题目1：二叉树的深度

题目链接：https://leetcode.cn/problems/er-cha-shu-de-shen-du-lcof/

2.1 题目介绍

输入一棵二叉树的根节点，求该树的深度。从根节点到叶节点依次经过的节点（含根、叶节点）形成树的一条路径，最长路径的长度为树的深度。

【测试用例】：
在这里插入图片描述

【条件约束】：

提示：

节点总数 <= 10000

【相关题目】：

注意：本题与主站 104. 二叉树的最大深度题目相同。

2.2 题解 – 递归 – O(n)

时间复杂度O(n)，空间复杂度O(n)

【解题思路】：
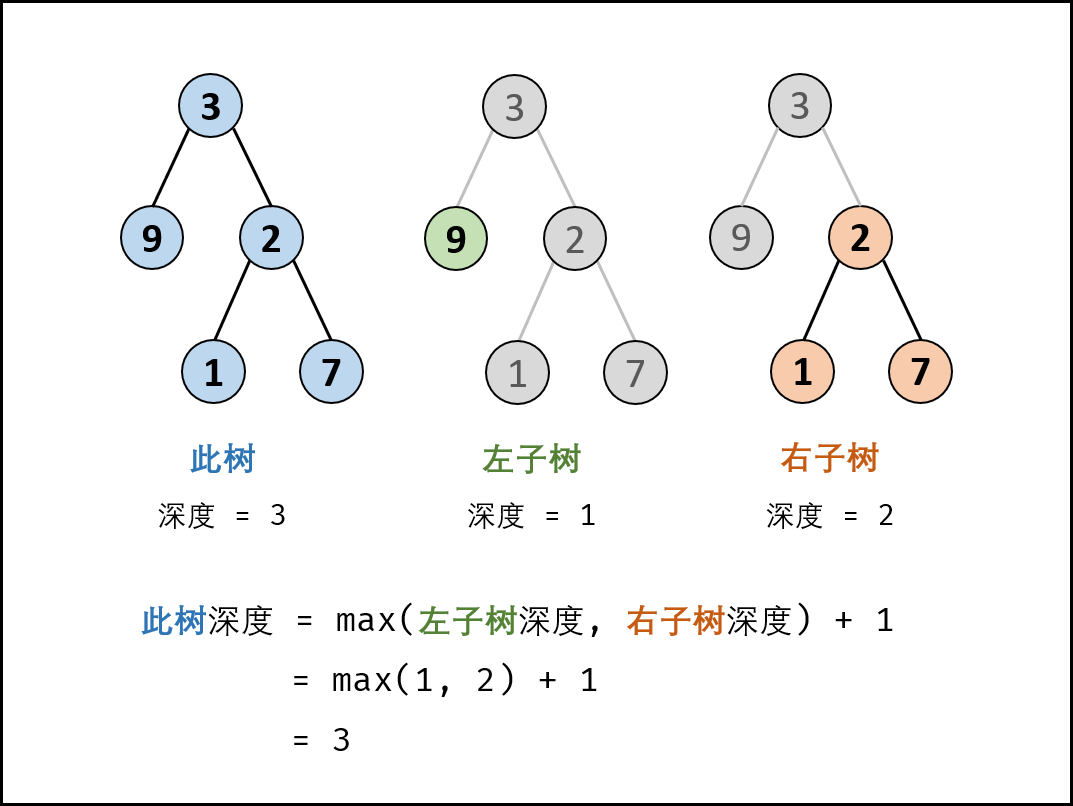
常规思路：遍历得到所有路径，并从中找出最长路径（可以用栈来实现）

简化思路：找出左右子树的深度，本质上属于后序遍历（用递归来实现）

如果一棵树 只有一个节点，那么它的深度为 1；
如果根节点 只有左子树 而没有右子树，那么树的深度应该是其左子树的深度加1；
同样，如果根节点 只有右子树 而没有左子树，那么树的深度应该是其右子树的深度加1；
如果 既有右子树又有左子树，那么该树的深度就是其左、右子树深度的 较大值 再加1.

……
【实现策略】：

首先还是进行无效输入判断，判断 根节点是否为空;
接着，我们通过递归来获取 左、右子树的深度；
最后，选择左、右子树深度的 较大值 再加1后，返回。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    // Solution1：递归
    public int maxDepth(TreeNode root) {
        // 无效输入判断
        if (root == null) return 0;
        // 递归获取左右子树深度
        int leftD = maxDepth(root.left);
        int rightD = maxDepth(root.right);
        // 返回树深
        return (leftD > rightD) ? leftD+1 : rightD+1;
    }
}

在这里插入图片描述

3. 题目2：平衡二叉树

3.1 题目介绍

输入一棵二叉树的根节点，判断该树是不是平衡二叉树。如果某二叉树中任意节点的左右子树的 深度相差不超过1 ，那么它就是一棵 平衡二叉树。

【测试用例】：
在这里插入图片描述

【条件约束】：

限制：

0 <= 树的结点个数 <= 10000

【相关题目】：

注意：本题与主站 110. 平衡二叉树题目相同。

3.2 题解 – 递归 – O(n)

时间复杂度O(n)，空间复杂度O(n)
在这里插入图片描述

【解题思路】：

平衡树(Balance Tree，BT) 指的是，任意节点的子树的 高度差 都小于等于1，即题目中的任意节点的左右子树的 深度相差不超过1。
那么，我们可以想到使用 后序遍历 ，来遍历二叉树的每个节点，在遍历到一个节点之前，我们就已经遍历了它的左、右子树。只要在 遍历每个节点的时候记录它的深度 ，我们就可以一边遍历一边判断每个节点是不是平衡的。
当然，我们也可以通过先序遍历 + 判断深度（从顶至底）的方法来判断该树是不是一棵平衡二叉树，但由于先序遍历是自顶向下的，会产生大量重复计算，时间复杂度较高，因此还是推荐使用 后序遍历（自底向下） 来解决该问题。
……
【实现策略】：

设置 递归终止条件，当递归到节点为空时，返回 0 ，代表当前节点深度为 0；
进行后序遍历的同时，记录下左、右子树的深度；
比较左、右子树的深度，判断当前树是不是一棵平衡二叉树，如果是则返回当前节点下的最大深度，如果不是返回 -1；
最后判断递归函数返回的值是不是 -1，如果不是，则说明该树是一棵平衡二叉树。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    // Solution1：后序遍历：可以保证节点不重复利用
    public boolean isBalanced(TreeNode root) {
        return recur(root) != -1;
    }
    // 递归
    private int recur(TreeNode root) {
        // 递归终止条件
        if (root == null) return 0;
        // 后序遍历
        int left = recur(root.left);
        if(left == -1) return -1;
        int right = recur(root.right);
        if(right == -1) return -1;
        // 如果左右子树的深度差不超过1，则说明该树是平衡二叉，返回其深度，如果超过，则返回-1
        return Math.abs(left - right) < 2 ? Math.max(left, right) + 1 : -1;
    }
}