排序-指标解读

news2025/1/18 8:53:26

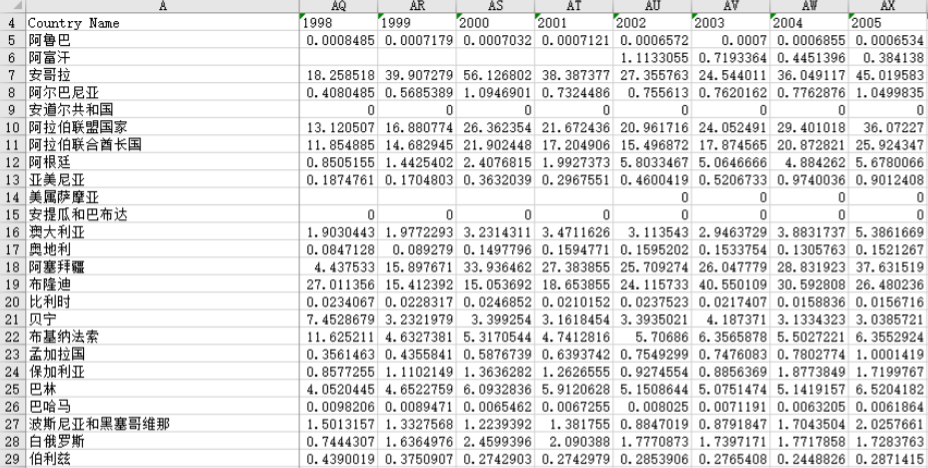
一、ROC

ROC曲线全称是(receiver operating characteristic cure)受试者工作特征曲线。

首先大家看到这里肯定会好奇，为啥名字这么奇怪，来一波背景介绍先。

“ROC起先应用于军事领域，据说在第二次世界大战期间，ROC 曲线最先是由战线前沿的电子工程师和雷达工程师联合发明的。雷达兵的任务很明确，就是盯着雷达显示屏，查看是否有敌机来袭（显然，有敌机和没有敌机是一个典型的二分类问题）。当然如果有飞鸟来袭，也会出现信号，如果过于谨慎有信号就报告，会增加误报风险，但如果过于大胆，凡是信号都认为是飞鸟这会出现很大风险。ROC曲线正是解决此类问题，即用于尽最大可能研究敌机信号和飞鸟信号之间的区别，以增加预报准确性。

于是嘞，军方的电子工程师汇总了所有雷达兵的预报数据，特别是漏报和误报的概率，并把这些概率一一绘制到一个二维坐标系中。这个坐标系的纵坐标为TPR（真阳性率，True Positive Rate），它表示敌机真的来袭时雷达兵能够预报正确的概率。横坐标为FPR（假阳性率，False Positive Rate，简称 FPR），它表示非敌机来袭（如飞鸟飞过）时，雷达兵将其误判为敌机来袭的概率。”

ok，基于以上背景，我相信大家都有了一定的背景铺垫了，这个里面引出了两个词TPR和FPR，我来在重解释一下。

TPR：代表纵坐标的值，该值的计算=(预测为正&&实际为正的样本数)/所有正样本数

FPR：代表横坐标的值，该值的计算=(预测为正&&实际为负的样本数)/所有负样本数

军官的期望是什么呢？他希望得到一个完全正确的分类，也就是当横坐标是0的时候，也就是所有的负样本都没有预测为正，此时的纵坐标对应的是1，也就是所有的正样本都预测为正。那么此时就不会误报了，模型很准确了，刚好可以分开，但是现实中的数据总会有交集，导致无法完全区分开。那我们如何判断这个雷达，或者说这个模型预测是否准确呢？就通过我们刚刚提到的roc曲线这个是方法，引出的auc这一概念来辅助我们判断雷达的预测准确率

二、AUC

AUC，不是我们经常提到的accuracy哈，是area under cure。

通过roc的方式，我们可以将现有的训练数据，计算纵坐标TPR和横坐标FPR，产生很多的点，通过描点连线，会产生如下的图，而其中的auc顾名思义，就是roc曲线下的面积，也就是阴影面积。

1>通过下图我们可以发现，什么时候是完美的模型？

当auc=1时，也就是全是阴影部分的时候，此时模型完美预测，也就是当横坐标是0的时候，纵坐标为1.

2>什么时候是个好模型？

0.5<auc<1时，这个区间比较常见。

3>当auc = 0.5的时候呢？

盲猜咯，已经没有什么价值了。

综上3点，也就是说auc越大越好，但是这么理解可能还是有点生硬，全体坐好，跟着我在升华一下理解！究竟这个auc也就是这个积分的面积，是啥呢？我们已经知道了是通过TPR和FPR围起来的面积了，但实际的意义是什么呢？

回归一下，TPR和FPR的概念，我们上图画的是归一化后的曲线，但如果不做归一化呢？假设有M个正样本，N个负样本，那纵坐标的最高点从1->M,横坐标的最远点从1->N。

auc = S(阴影面积)/S(矩形面积)

阴影面积代表着:这个正样本预测为正的概率在多少个负样本前，它的后面有多少个负样本。

这里再具体一点，就是每个样本会有个模型预测的概率，[0-1]之间，假设(完美模型的例子)

3个正样本的概率: 0.9,0.8,0.7 4个负样本的概率是:0.6,0.5,0.2,0.1

那么此时当我们选阈值为0.9时，就是我们用0.9来做分界线，我们认为预测概率大于等于0.9才是正样本，预测概率小于0.9就是负样本，此时当阈值是0.9时，该正样本后有4个负样本。

一种极端情况就是，当横坐标是0时，也就是没有样本实际为负但预测为正，此时，纵坐标是M，也就是所有的正样本都预测为正。也就是说，完美模型，正负样本完全分开。

那整个矩形面积就从1*1->M*N。

极端情况下，完美模型，auc=（遍历所有正样本，每个正样本都比N个负样本大）/M*N

= M次的N相加/M*N = 1

代码层面，这个原理，就是上面的升华理解，有不太理解的地方，欢迎踊跃留言哈！:

true_arr = [1, 1, 1, 1, 1, 0, 0, 0, 0]
pred_arr = [0.9, 0.8, 0.7, 0.6, 0.6, 0.5, 0.4, 0.3, 0.2]
def cal_auc(true_arr, pred_arr):
    #首先按照概率从高到低排序
    list_ori = []
    for i in range(len(true_arr)):
        list_ori.append((true_arr[i],pred_arr[i]))
    new_list = sorted(list_ori,key = lambda x:x[1],reverse = True)
    print(new_list)
    auc = 0
    #正样本个数M，负样本个数N
    M,N = 0,0
    #Z代表，负样本前有多少个正样本，和正样本之后有多少个负样本
    Z = 0
    for item in new_list:
        #如果是负样本的话
        if item[0] == 0:
            N += 1
            Z += M
        elif item[0] == 1:
            M += 1
    auc = Z/(M*N)
    return auc
cal_auc(true_arr,pred_arr)