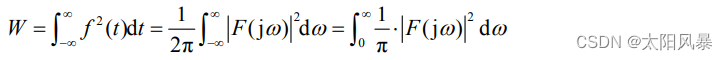傅立叶变换的性质与应用
- 一、傅里叶变换性质表
- 二、傅里叶性质详细
- 1. 线性性质
- 2. 尺度变换特性
- 3. 时移特性
- 4. 频移特性
- 5. 时域微分特性
- 6. 频域微分特性
- 7. 时域积分特性
- 8. 频域积分特性
- 9. 卷积定理
- 1. 时域卷积定理
- 2. 频域卷积定理
- 10. 对称性
- 11. 帕塞瓦尔定理
依据傅里叶变换对概念,一个非周期连续时间信号可以表述为指数函数的积分。根据这个积分的性质可以联系起时域和频域的关系。推导出一些非常好用的公式,以简化运算。
一、傅里叶变换性质表

二、傅里叶性质详细
- 傅里叶变换式:

该变换式建立起了信号时域与频域间的联系,因而,一个信号可以有两种描述,而且形式可以相互转换,这里主要记录一下信号在时域中进行运算或变化时,在频域引起的效应。
1. 线性性质
用这个就能复合信号分解,然后分别求单独的傅里叶变换,最后再合并,主要就是分解来分步骤解决问题。和LTI 的线性齐次变换一致的。
- 定义:

例题:

2. 尺度变换特性
尺度变换特性说明,连续时间信号在时域展宽(0 < a < 1),对应其频谱信号在频域压缩;时域压缩(a >1),对应频域展宽;如果a < 0 ,则时域波形反转并压缩或展宽。这一特性说明了时间和频率之间的反比关系,通常称为时频展缩。
(F = 1 / T) 所以成反比哈
该性质在信号处理系统设计时,常常是一重要的衡量因素。例如,希望提高系统的传输效率时,需要对待传输的信号进行压缩,但压缩后的信号则需要设计频带更宽的传输系统。
- 定义:

证明:

例题:

3. 时移特性
这一性质说明,当信号在时间域有移位(表示信号的接入时间有变化),其幅度频谱不变,相位频谱将增加一个附加相移 ±ωt0,并且与ω 成线性关系。
- 定义:

证明:

例题:

4. 频移特性
这个用的非常多,他能频谱搬移,用的非常多。
- 定义:

证明:

例题:

频移特性在各类电子系统中应用广泛,如调幅、同步解调等都是在频谱搬移基础上实现的,实现频谱搬移的原理如下图所示。它将信号 f(t) (常称为调制信号)在时域上乘以载波信号 cos(ω0t) 或 sin(ω0t) ,从而得到高频已调信号 y(t) ,即
- y(t) = f(t) · cos(ω0t)

下面举出门函数及高频脉冲信号的时域波形及其频谱例子

可见,当用某低频信号 f (t) 去调制角频率为 ω0 的正弦信号的振幅时,高频已调信号的频谱是将 f (t) 的频谱 F(jω) 按比例复制为二,分别向左和向右搬移 ω0 ,在搬移的过程中,幅度频谱的形式未改变。上述频率搬移的过程,在电子技术中就是调幅的过程。
5. 时域微分特性
时域的微分运算用频域中的乘法运算代替,这样就简化运算了
- 定义:

证明:

例题:

6. 频域微分特性
- 定义:

证明:

7. 时域积分特性
- 定义:

例题:


8. 频域积分特性
- 定义:

例题:

9. 卷积定理
1. 时域卷积定理
两个时域内相卷积信号的傅里叶变换为其分别求频谱的乘积。通过这一性质,我们可以将时域的卷积运算映射到频域进行。
- 定义:

证明:

2. 频域卷积定理
一个信号乘以另一个信号,可以理解为用一个信号去调制另一个信号的振幅,因此,频域卷积定理有些书上也称为(幅度)调制定理
- 定义:

例题:

例题:

10. 对称性
该性质说明,时间变量和频率变量交换后,都有一种对称关系(也称对偶关系)存在。利用这一性质,可以比较方便地分析某些信号的傅里叶正变换和傅里叶反变换。
- 定义:

证明:

例题:

11. 帕塞瓦尔定理
- 定义:

一般来说,非周期信号不是功率信号,其平均功率为零,但其能量为有限值,故是一个能量信号,其总能量W 为

非周期信号的帕塞瓦尔定理表明:对于非周期信号而言,在时域中求得的信号能量与在频域中求得的信号能量相等。由于|F(jw)|2 是 w 的偶函数, 也可以写做: