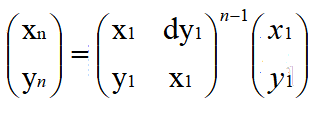给定两个整数 a 和 b ，求它们的除法的商 a/b ，要求不得使用乘号 '*'、除号 '/' 以及求余符号 '%' 。

注意：

• 整数除法的结果应当截去（truncate）其小数部分，例如：truncate(8.345) = 8 以及 truncate(-2.7335) = -2
• 假设我们的环境只能存储 32 位有符号整数，其数值范围是 [−231, 231−1]。本题中，如果除法结果溢出，则返回 231 − 1

输入：a = 15, b = 2
输出：7
解释：15/2 = truncate(7.5) = 7

力扣https://leetcode.cn/problems/xoh6Oh/description/思路:不断寻找当前最大的可被减掉但是被除数剪完不会小于零的数,这个搜索过程类似二分法.

本题思路其实很简单,就是用减法代替除法.主要优化在减数的选择上.

算法流程:

        1.初始化结果re = 0;

        2.如果被除数大于除数,则除数扩大一倍

        3.如果被除数仍然大于除数,则继续扩大一倍.

        4.直到除数下一次翻倍的时候大于被除数,则被除数减掉此时的除数(剪完的结果是大于零的),将倍数累加到re中,结束当前轮次的循环.

        5.重复上述步骤,直到被除数小于除数.

在整个过程中要注意一点:

        java的int范围,-2 ^ 31,2 ^ 31−1,所以负数转整数会存在越界问题(负数比正数的范围大1),同时要注意,如果a,b一正一负,那么结果要取反

        不用abs函数的原因也在于如果a = -2 ^ 31,abs会报错的

class Solution {
    public int divide(int a, int b) {
        int flag = 0;
        if(a > 0){
            a = -a;
            flag += 1;
        }
        if(b > 0){
            b = -b;
            flag += 1;
        }

        int res = cal(a, b);
        
        if(flag != 1 && res == Integer.MIN_VALUE ){
            res += 1;
        }

        return flag == 1 ? res : -res; 
    }

    public int cal(int a ,int b){
        int re = 0;
        while ( a <= b){
            int maxData = b;
            int num = 1;
            while(maxData >= Integer.MIN_VALUE >> 1 && a <= maxData << 1){
                maxData += maxData;
                num += num;
            }
            a -= maxData;
            re -= num;
        }
        return re;
    }
}