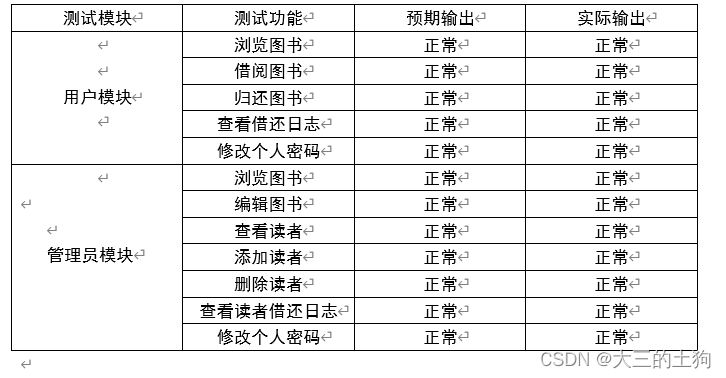
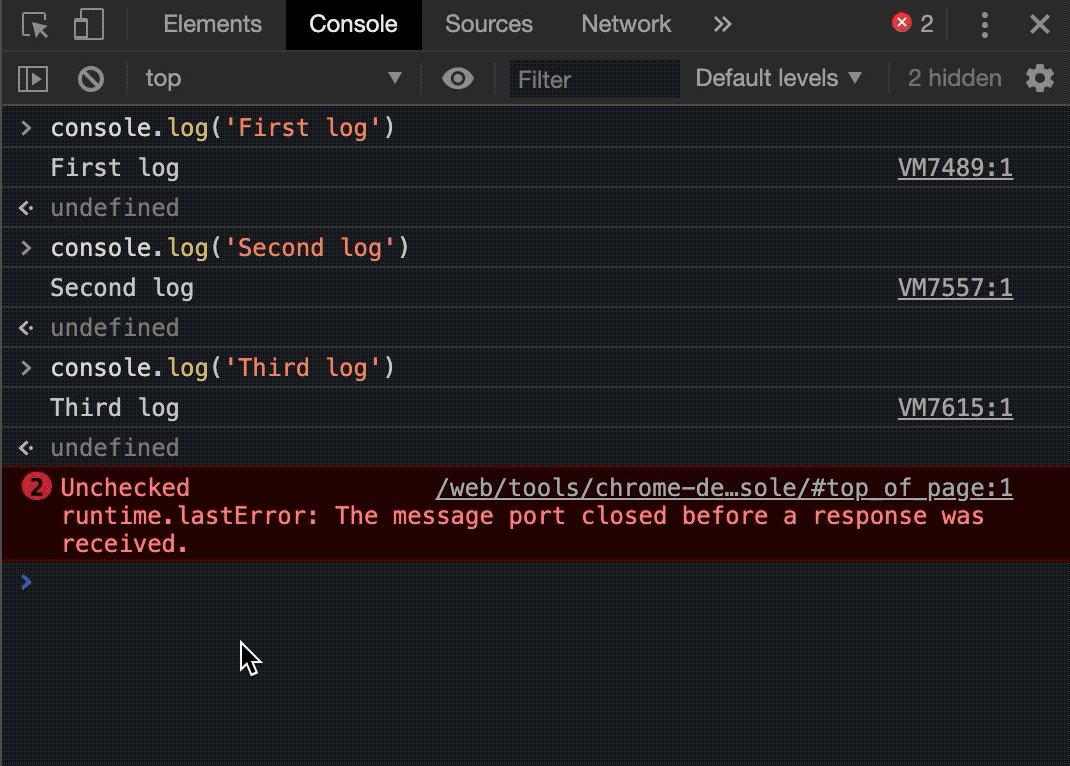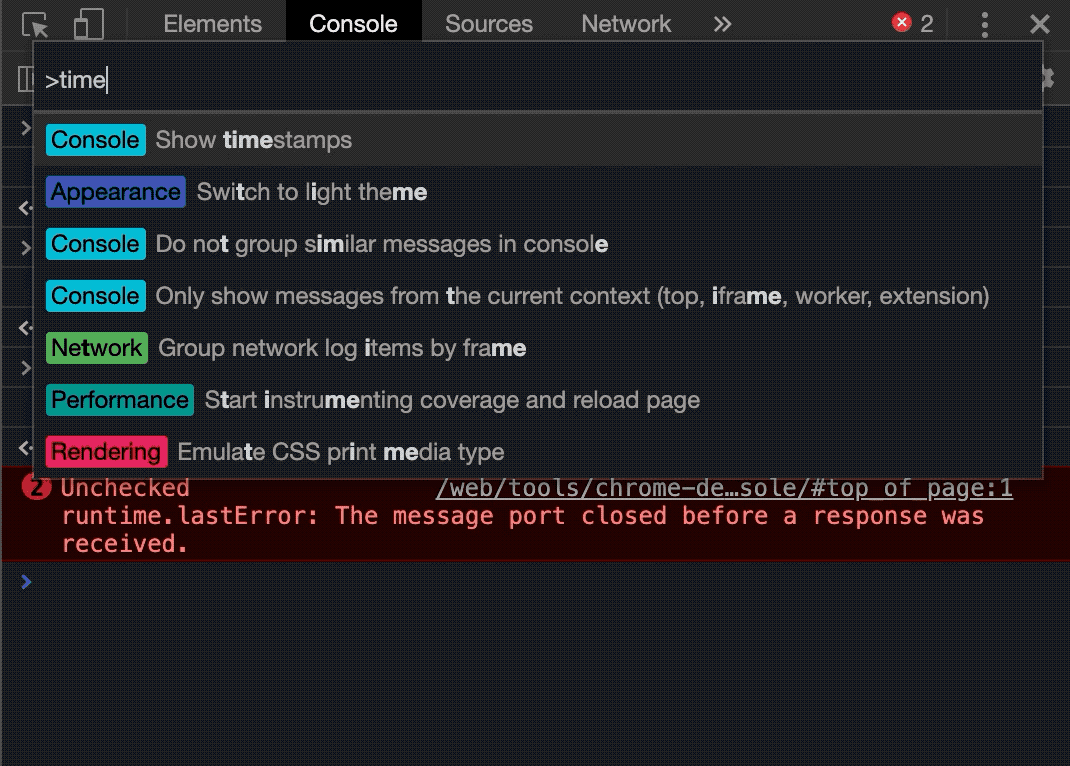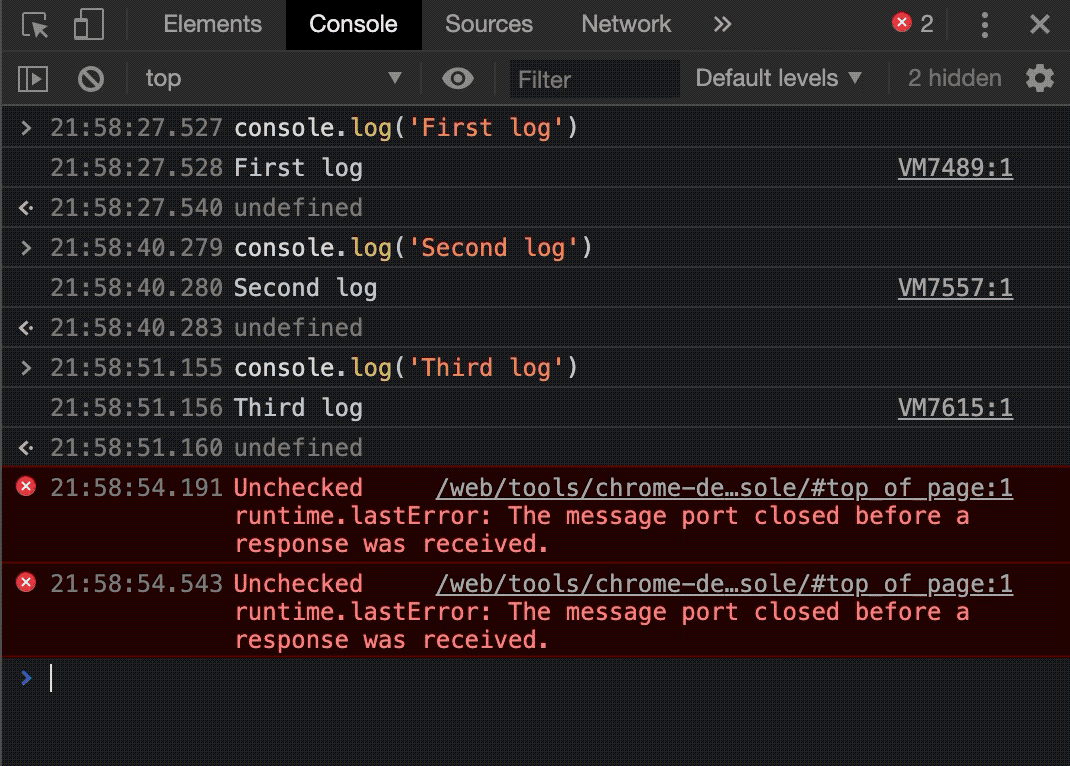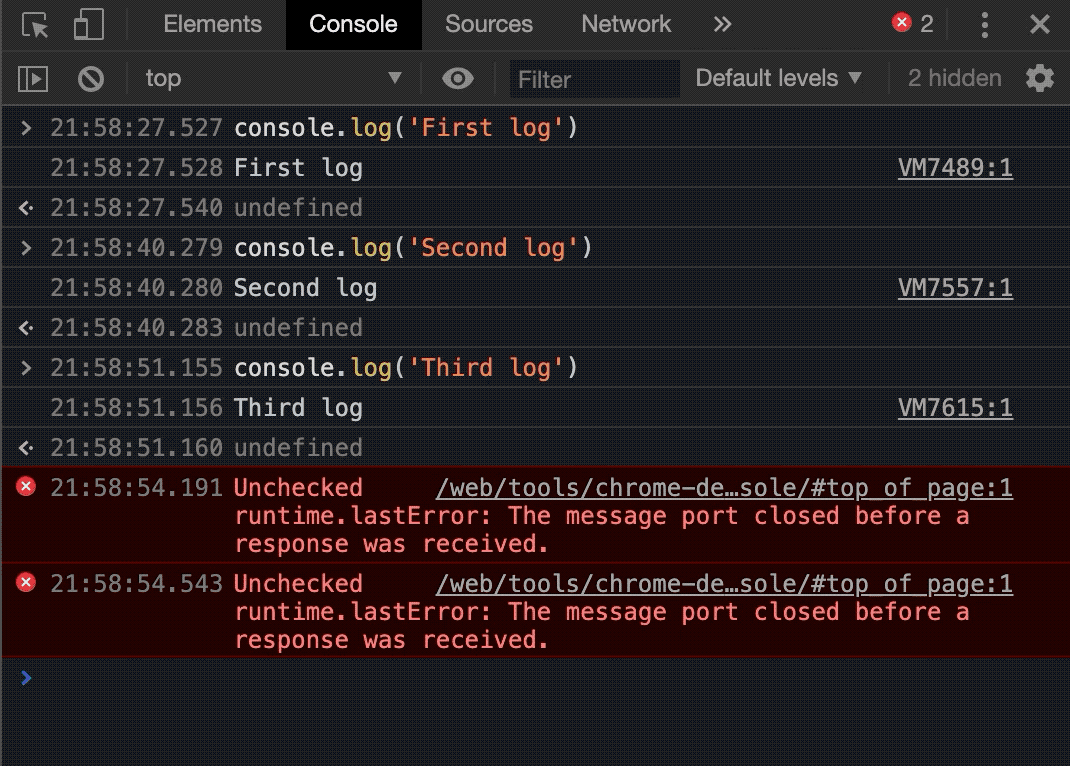
这周我来总结一下数论分块和佩尔方程：

已知正整数n，求，对n/i下取整，相当于把一组数分块了，首先我们来找一下规律：n=20时

1    2   3  4  5  6  7  8  9  10  11  12  13  14  15  16  17  18  19  20                                                  20 10  6  5  4  3  2  2  2   2    1    1    1    1    1    1    1    1    1    1

一个明显的规律时存在多个区间，使得某个区间内，有连续的  数值相同，如果设某个区间的左端点是L，那么这个区间的右端点就是n/  ；如上，如果L=7，那么n/  =10

若求*i，在一段区间内n/i的值是相同的，∑i的求和是一个明确了左端点和右端点的等差数列求和，∑i=n*(a1+a2)/2，n为区间长度，a1是左端点，a2是右端点

例题：1、约数研究 P1403 [AHOI2005]约数研究 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

每个正约数  在 1 ~ n 中出现的次数为  ，所以问题可以转换成求 的值，套用模板即可。

 2、约数和P2424 约数和 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

问题就转换成了求  ，可以分块处理，用等差数列的求和可以得到答案，注意求的是  区间的答案，可以转换成求 。

 佩尔方程：

第一类：x2−dy2=1

1)如果d为平方数时，此时只有x = 1或-1，y=0，这两组特定解。2)当d不为平方数时，方程有无穷多组整数解。

第二类：x2−dy2=k

对于佩尔方程这周开了个头，了解了佩尔方程的背景形式，

可以用矩阵快速幂求解，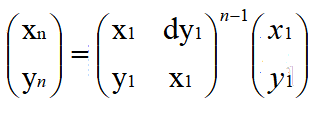

暴力求解：

void search(int d,int &x,int &y) //x^2 - d*(y^2) = 1
{
	y=1;
	while(1)
	{
		x=(long long )sqrt(d*y*y+1);
		if(x*x-d*y*y==1)
			break;
		y++;
	}
}