目录
1.每日一句
2.作者简介
『LeetCode|每日一题』最小路径和
1.每日一题
2.解题思路
2.1 思路分析
2.2 核心代码
2.3 完整代码
2.4 运行结果
1.每日一句
希望冬天的风能吹散一年里所有的遗憾
2.作者简介
🏡个人主页:XiaoXiaoChen-2716
📚学习专栏:力扣专栏
🕒发布日期:2022/11/27

『LeetCode|每日一题』最小路径和
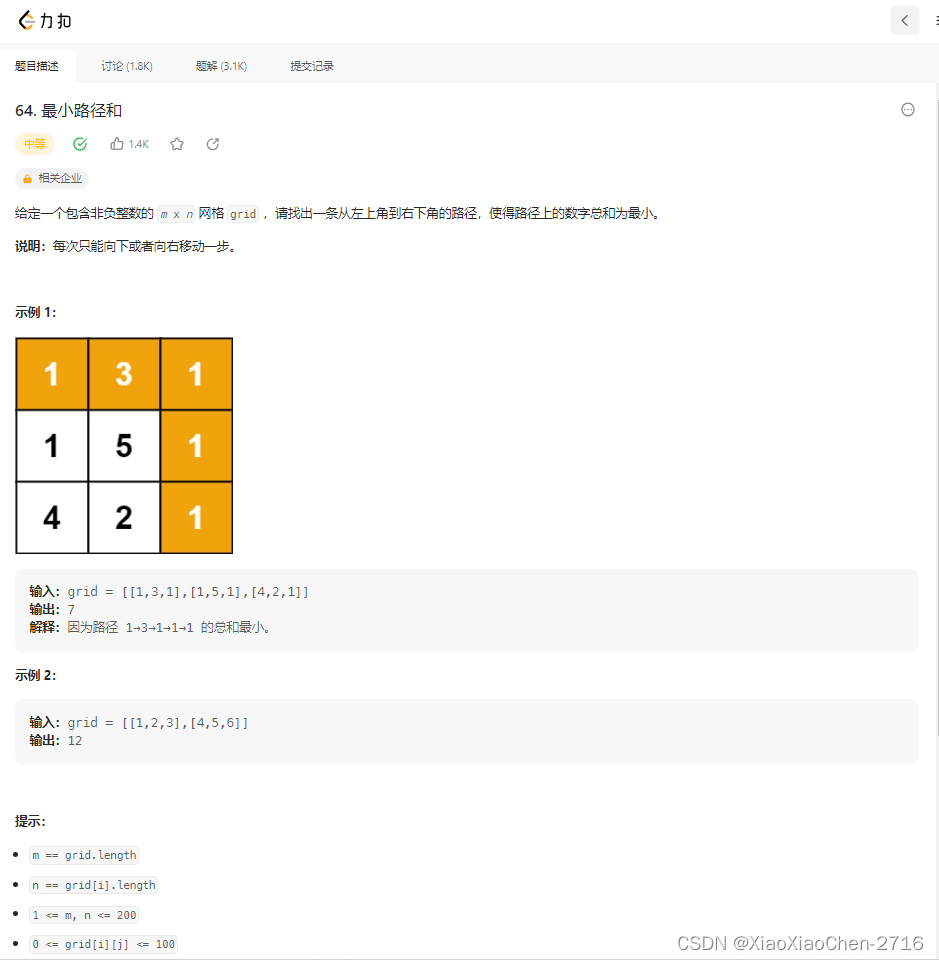
1.每日一题
原文链接--->点我
2.解题思路
2.1 思路分析
典型的动态规划题,相信很多小伙伴可以用一个dp数组轻松解决,但是也可以在原数组上改动,这样空间复杂度就只有O(1)了
S1:首先是特殊情况判断,矩阵为空的情况就直接返回0即可;
S2:因为终点已经规定了,方向也已经规定了,所以第一列和第一行的所有位置的值都是确定的,我们用两个for循环就可以初始化了;
S3:接下来就是动态规划的方程式,我们每次选取当前位置的左边或者上面值小的那个就可以了,用一个双层for循环即可实现,当前位置i , j,那么它的上面就是i - 1 , j,它的左边位置就是i , j - 1,选最小的那个即可;
S4:最后返回矩阵右下角的位置的值即可
2.2 核心代码
for(int i = 1 ; i < col ; i++){
for(int j = 1 ; j < row ; j++){
grid[i][j] = Math.min(grid[i - 1][j] , grid[i][j - 1]) + grid[i][j];
}
}2.3 完整代码
class Solution {
public int minPathSum(int[][] grid) {
int col = grid.length; //行
int row = grid[0].length; //列
if(col == 0 && row == 0) return 0;
for(int i = 1 ; i < col ; i++){
grid[i][0] += grid[i - 1][0];
}
for(int i = 1 ; i < row ; i++){
grid[0][i] += grid[0][i - 1];
}
for(int i = 1 ; i < col ; i++){
for(int j = 1 ; j < row ; j++){
grid[i][j] = Math.min(grid[i - 1][j] , grid[i][j - 1]) + grid[i][j];
}
}
return grid[col - 1][row - 1];
}
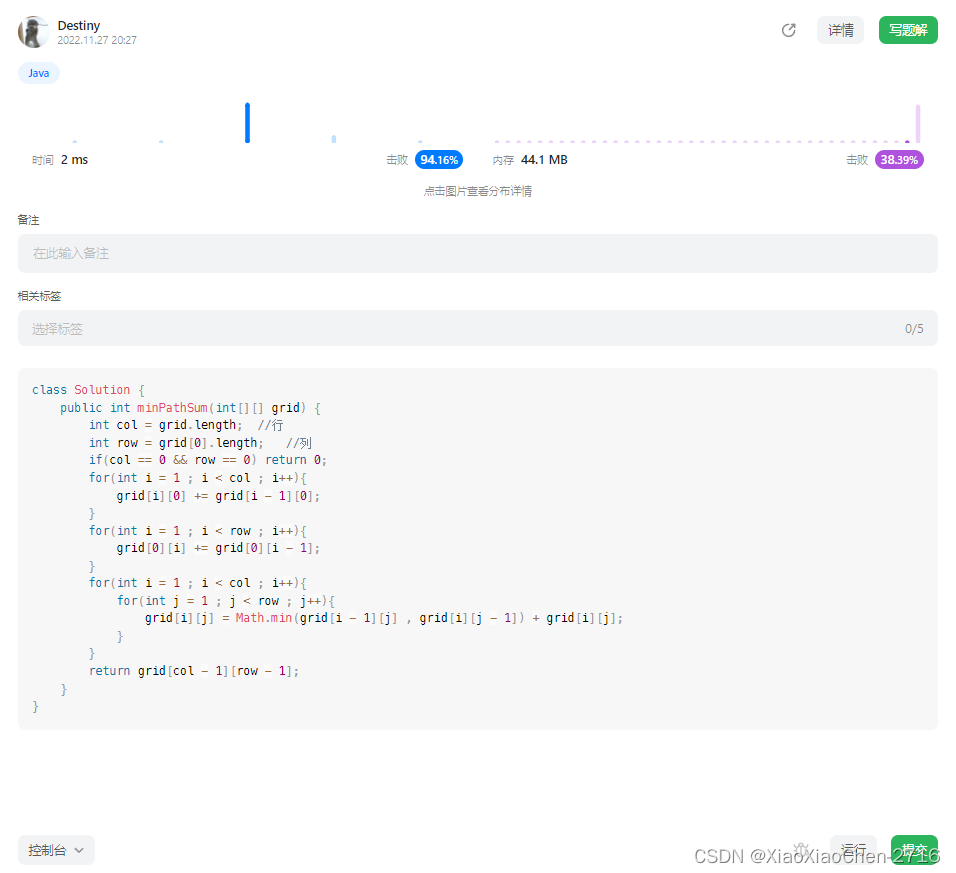
}2.4 运行结果
🍁 类似题目推荐:
1.数据结构基础
2.算法专项练习
3.剑指offer专项练习
4.推荐一个学习网站:LeetCode,算法的提升在于日积月累,只有每天练习才能保持良好的状态
如果文章对各位大佬有帮助就支持一下噢,不好的地方请各位大佬多多指教!