队列——算法专项刷题（七）

七、队列

常用于辅助遍历树，设计队列先进先出特性的数据结构

7.1 滑动窗口的平均值

给定一个整数数据流和一个窗口大小，根据该滑动窗口的大小，计算滑动窗口里所有数字的平均值。

实现 MovingAverage 类：

MovingAverage(int size) 用窗口大小 size 初始化对象。
double next(int val) 成员函数 next 每次调用的时候都会往滑动窗口增加一个整数，请计算并返回数据流中最后 size 个值的移动平均值，即滑动窗口里所有数字的平均值。

示例：

输入：
inputs = [“MovingAverage”, “next”, “next”, “next”, “next”]
inputs = [[3], [1], [10], [3], [5]]
输出：
[null, 1.0, 5.5, 4.66667, 6.0]

解释：

MovingAverage movingAverage = new MovingAverage(3);
movingAverage.next(1); // 返回 1.0 = 1 / 1
movingAverage.next(10); // 返回 5.5 = (1 + 10) / 2
movingAverage.next(3); // 返回 4.66667 = (1 + 10 + 3) / 3
movingAverage.next(5); // 返回 6.0 = (10 + 3 + 5) / 3

提示：

1 <= size <= 1000
-105 <= val <= 105
最多调用 next 方法 104 次

思路： 使用队列定义一个size表示队列最大元素个数，如果在添加元素时，队列元素个数等于size，就出队一个元素，再添加。维护一个sum，记录队列中元素和

注意点： sum最好直接定义为浮点类型

class MovingAverage {

    Queue<Integer> queue;
    int size;
    double sum;

    /**
     * Initialize your data structure here.
     */
    public MovingAverage(int size) {
        queue = new LinkedList<>();
        this.size = size;
        sum = 0.0;

    }

    public double next(int val) {

        if(queue.size() == size){
            sum = sum - queue.poll();
        }
        
        queue.offer(val);
            sum += val;

        return sum / queue.size();

    }
}

7.2 最近请求次数

原题链接

写一个 RecentCounter 类来计算特定时间范围内最近的请求。

请实现 RecentCounter 类：

RecentCounter() 初始化计数器，请求数为 0 。
int ping(int t) 在时间 t 添加一个新请求，其中 t 表示以毫秒为单位的某个时间，并返回过去 3000 毫秒内发生的所有请求数（包括新请求）。确切地说，返回在[t-3000, t]内发生的请求数。

保证每次对 ping 的调用都使用比之前更大的 t 值。

示例：

输入：
inputs = [“RecentCounter”, “ping”, “ping”, “ping”, “ping”]
inputs = [[], [1], [100], [3001], [3002]]
输出：
[null, 1, 2, 3, 3]

解释：

RecentCounter recentCounter = new RecentCounter();
recentCounter.ping(1); // requests = [1]，范围是 [-2999,1]，返回 1
recentCounter.ping(100); // requests = [1, 100]，范围是 [-2900,100]，返回 2
recentCounter.ping(3001); // requests = [1, 100, 3001]，范围是 [1,3001]，返回 3
recentCounter.ping(3002); // requests = [1, 100, 3001, 3002]，范围是 [2,3002]，返回 3

提示：

1 <= t <= 109
保证每次对 ping 调用所使用的 t 值都 严格递增
至多调用 ping 方法 104 次

思路： 使用队列数据结构，在ping时先将不符合的条件的值出队，然后返回队列元素个数即为符合条件的

注意点： 无

class RecentCounter {

    Queue<Integer> queue;

    public RecentCounter() {
        queue = new ArrayDeque<>();
    }

    public int ping(int t) {
  int num = t - 3000;
  while(!queue.isEmpty() && queue.peek() < num){
      queue.poll();
  }
  queue.offer(t);
        
  return queue.size();
        
    }
}

7.3往完全二叉树添加结点

完全二叉树是每一层（除最后一层外）都是完全填充（即，节点数达到最大，第 n 层有 2n-1 个节点）的，并且所有的节点都尽可能地集中在左侧。

设计一个用完全二叉树初始化的数据结构 CBTInserter，它支持以下几种操作：

CBTInserter(TreeNode root) 使用根节点为 root 的给定树初始化该数据结构；
CBTInserter.insert(int v) 向树中插入一个新节点，节点类型为 TreeNode，值为 v 。使树保持完全二叉树的状态，并返回插入的新节点的父节点的值；
CBTInserter.get_root() 将返回树的根节点。

示例 1：

输入：inputs = [“CBTInserter”,“insert”,“get_root”], inputs = [[[1]],[2],[]]
输出：[null,1,[1,2]]

提示：

最初给定的树是完全二叉树，且包含 1 到 1000 个节点。
每个测试用例最多调用 CBTInserter.insert 操作 10000 次。
给定节点或插入节点的每个值都在 0 到 5000 之间。

思路： 通过辅助队列层序遍历，将所有结点放入list集合中。由于完全二叉树的特性，若父节点序号为i，那么子节点序号为 2i，2i+1，因此我们通过list集合size /2 -1 就是父节点下标（下标从0开始需要-1）

注意点：先添加子节点，然后再根据 size /2-1计算父节点下标（（2i/2） -1 、（2i+1/2）-1）

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */

class CBTInserter {

    List<TreeNode> list;
    Queue<TreeNode> queue;
  
    public CBTInserter(TreeNode root) {
        list = new ArrayList();
        queue = new LinkedList();
        
      
          queue.offer(root);
          
          while(!queue.isEmpty()){
               TreeNode node = queue.poll();
              list.add(node);
               if(node.left != null){
                   queue.offer(node.left);
               }
                if(node.right != null){
                   queue.offer(node.right);
               }
          }

    }

    public int insert(int v) {
    TreeNode node = new TreeNode(v);
     list.add(node);
    // 结点 个数 /2 -1 就是 父节点下标 
         TreeNode parent= list.get(list.size() / 2 - 1);
         

         if(parent.left == null){
             parent.left = node;
         }else if(parent.right == null){
             parent.right = node;
         }
         
         return parent.val;
         

    }

    public TreeNode get_root() {
  
        return list.get(0);

    }
}

7.4二叉树的右侧视图

原题链接

给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

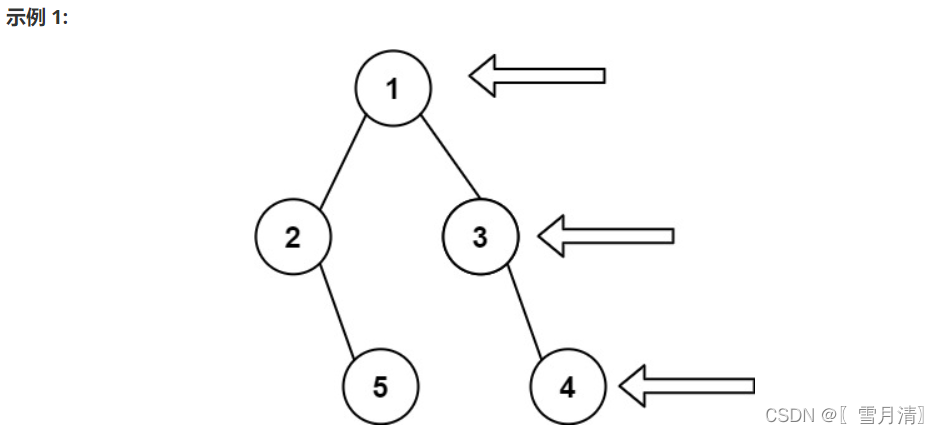
在这里插入图片描述

输入: [1,2,3,null,5,null,4]
输出: [1,3,4]

提示:

二叉树的节点个数的范围是 [0,100]
-100 <= Node.val <= 100

思路： 层序遍历，每一层的最后一个结点即为所求。使用队列辅助层序遍历，维护一个count记录每层结点的个数，如果为0，就表示当前结点就是每一层最后一个结点，并使用队列长度更细count

注意点： count为每层的结点个数，并非队列中的节点个数，只有当一层遍历结束的时候，count为0才会使用队列长度更新count

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> rightSideView(TreeNode root) {

        Queue<TreeNode> queue = new LinkedList();
        List<Integer> list = new ArrayList();

        if(root == null) return list;

        int count = 1;
        queue.add(root);
        while (!queue.isEmpty()){
             TreeNode node = queue.poll();
             count--;
             
             if(node.left != null){
                 queue.offer(node.left);
                
             }
             if(node.right != null){
                 queue.offer(node.right);
                
             }
             if(count == 0){
                 // 遍历完一层 更新count 并记录最后一个结点
                 list.add(node.val);
                 count = queue.size();
             }

        }
        
        return list;



    }
}

7.5二叉树每层的最大值

给定一棵二叉树的根节点 root ，请找出该二叉树中每一层的最大值。

示例1：

输入: root = [1,3,2,5,3,null,9]
输出: [1,3,9]
解释:

1

/ \

3 2

/ \ \

5 3 9

提示：

二叉树的节点个数的范围是 [0,104]
-231 <= Node.val <= 231 - 1

思路： 二叉树层序遍历，维护一个count记录每层结点个数，遍历每层时，一直更新max，在每层遍历结束，添加max，重置max和count

注意点： max在count为0就是每层遍历结束后要重新置为最小值

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> largestValues(TreeNode root) {

  Queue<TreeNode> queue = new LinkedList();

  List<Integer> list = new ArrayList();
  if(root == null) return list;
  queue.offer(root);
  // 表示每层元素
     int count = 1;
     int max = Integer.MIN_VALUE;
       
       while(!queue.isEmpty()){
       
           TreeNode node =  queue.poll();
              count--;

              max = Math.max(max,node.val);

              if(node.left != null){
                  queue.offer(node.left);
              }
              if(node.right != null){
                  queue.offer(node.right);
              }
              if(count == 0){
                  // 加入每层最大值
                  list.add(max);
                  // 重置 max 和 count
                  max = Integer.MIN_VALUE;
                  count = queue.size();
              }
           

       }

       return list;


    }
}

7.6二叉树最底层最左边的值

给定一个二叉树的 根节点 root，请找出该二叉树的 最底层最左边 节点的值。

假设二叉树中至少有一个节点。

示例 1:

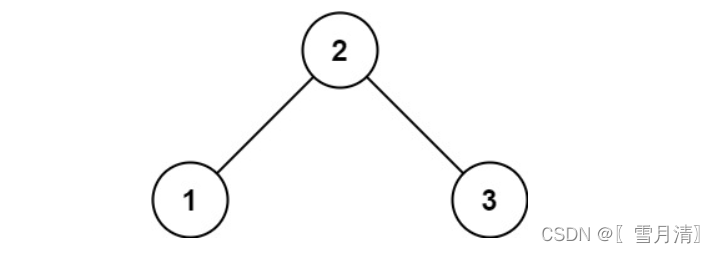
在这里插入图片描述

输入: root = [2,1,3]
输出: 1

提示:

二叉树的节点个数的范围是 [1,104]
-231 <= Node.val <= 231 - 1

思路： 深度优先遍历，维护一个curHight记录二叉树的最大高度，在dfs的时候计算更新当前遍历的高度hight，如果hight大于curHight说明遍历到了新的一层，此时的结点就是这一层最左边的结点

注意点： 先遍历左节点

class Solution {
    int curHight = 0;
    int cur = 0;
    public int findBottomLeftValue(TreeNode root) {
       

           dfs(root,0);

           return cur;


    }

    void dfs(TreeNode node, int hight){
        if(node == null) return;
       
        // 更新高度
        hight++;
        if(hight > curHight){
            curHight = hight;
            cur = node.val;
        }

        dfs(node.left,hight);
        dfs(node.right,hight);


    }
}