基于三相坐标系状态方程的感应电动机起动动态计算matlab程序
1 异步电动机动态数学模型的性质
电磁耦合是机电能量转换的必要条件,电流与磁通的乘积产生转矩,转速与磁通的乘积得到感应电动势。无论是直流电动机,还是交流电动机均如此。
交、直流电动机结构和工作原理的不同,其表达式差异很大。
异步电动机的动态数学模型是一个高阶、非线性、强耦合的多变量系统。
(1)异步电动机变压变频调速时需要进行电压(或电流)和频率的协调控制,有电压(或电流)和频率两种独立的输入变量。在输出变量中,除转速外,磁通也是一个输出变量。
(2)异步电动机无法单独对磁通进行控制,电流乘磁通产生转矩,转速乘磁通产生感应电动势,在数学模型中含有两个变量的乘积项。
(3)三相异步电动机三相绕组存在交叉耦合,每个绕组都有各自的电磁惯性,再考虑运动系统的机电惯性,转速与转角的积分关系等,动态模型是一个高阶系统。
2 异步电动机的三相数学模型
作如下的假设:(1)忽略空间谐波,三相绕组对称,产生的磁动势沿气隙按正弦规律分布。(2)忽略磁路饱和,各绕组的自感和互感都是恒定的。(3)忽略铁心损耗。(4)不考虑频率变化和温度变化对绕组电阻的影响。无论异步电动机转子是绕线型还是笼型的,都可以等效成三相绕线转子,并折算到定子侧,折算后的定子和转子绕组匝数相等。异步电动机三相绕组可以是Y连接,也可以是Δ连接。若三相绕组为Δ连接,可先用Δ—Y变换,等效为Y连接。然后,按Y连接进行分析和设计。定子三相绕组轴线A、B、C在空间是固定的。转子绕组轴线a、b、c随转子旋转。
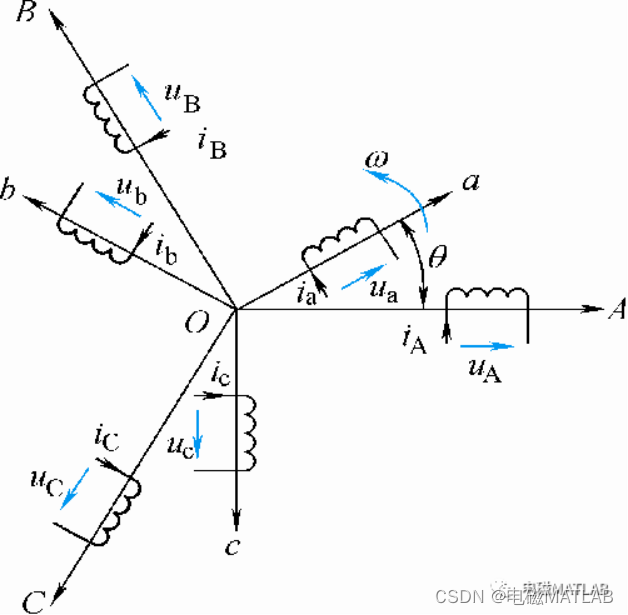
异步电动机的动态模型由磁链方程、电压方程、转矩方程和运动方程组成。磁链方程和转矩方程为代数方程,电压方程和运动方程为微分方程。
2.1 磁链方程异步电动机每个绕组的磁链是它本身的自感磁链和其它绕组对它的互感磁链之和.
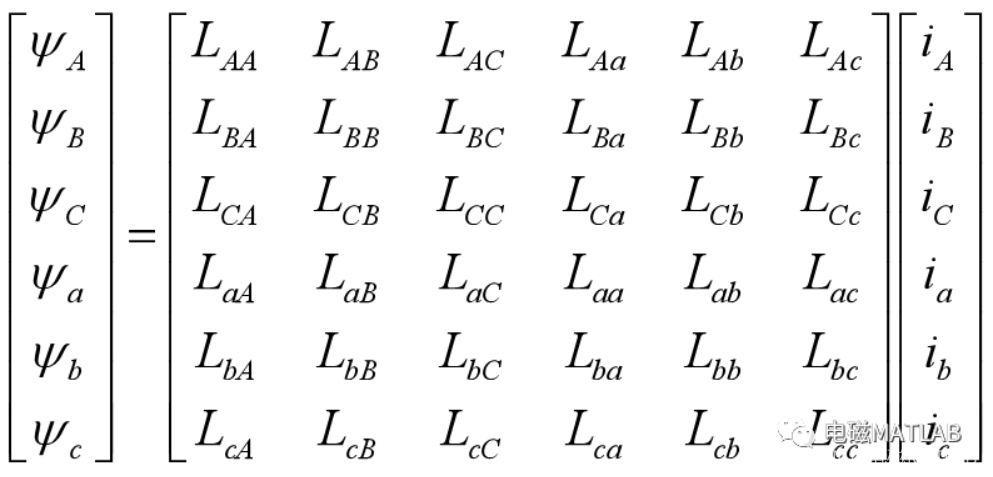
2.1.1 自感
定子各相自感

转子各相自感

2.1.2互感
绕组之间的互感又分为两类:①定子三相彼此之间和转子三相彼此之间位置都是固定的,故互感为常值;②定子任一相与转子任一相之间的相对位置是变化的,互感是角位移的函数。
定子三相间或转子三相间互感
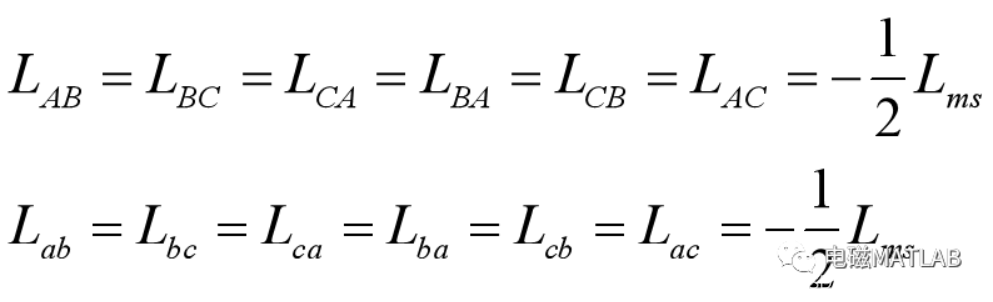
定、转子绕组间的互感
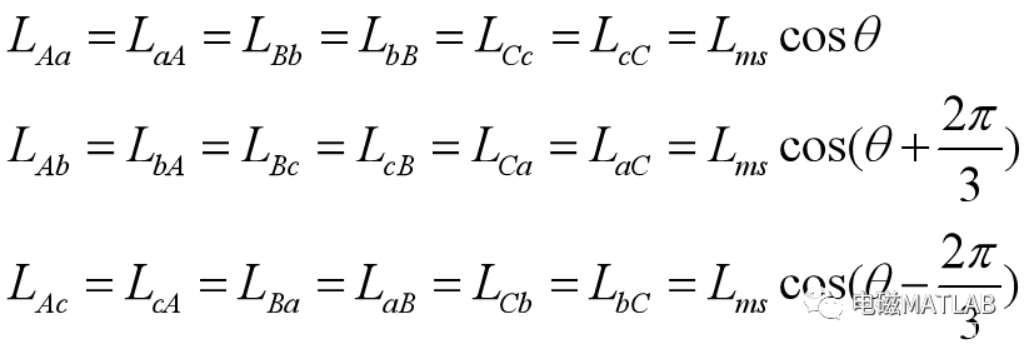
2.2 电压方程
三相绕组电压平衡方程
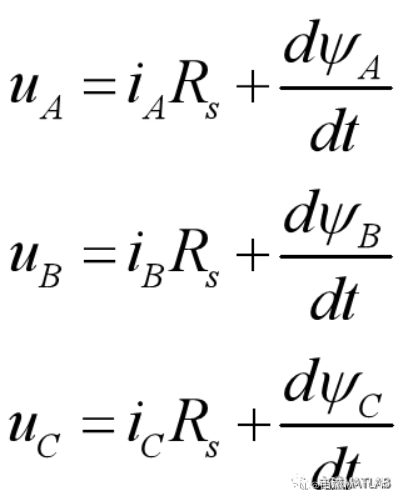
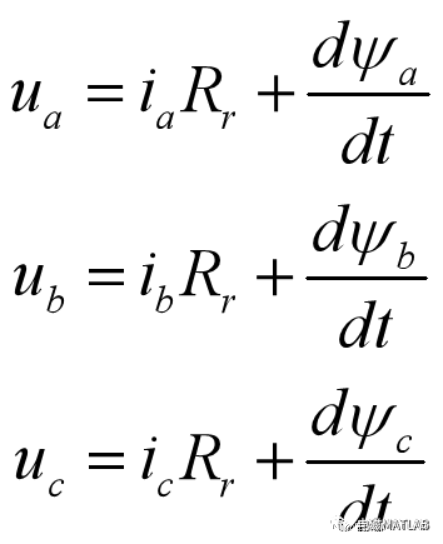
将电压方程写成矩阵形式


把磁链方程代入电压方程,展开
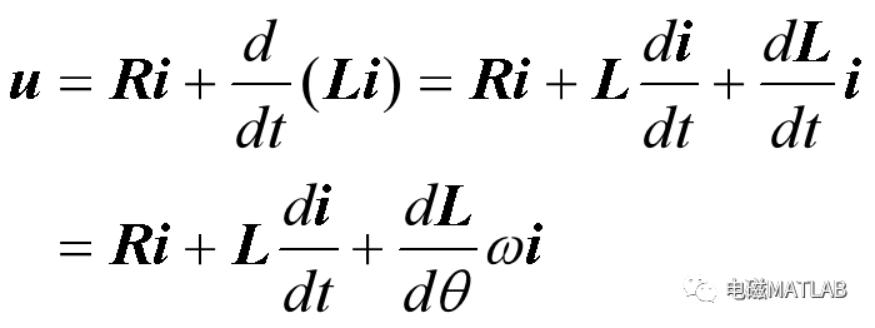
2.3 转矩方程和运动方程
转矩方程

运动方程

转角方程

2.4 动态数学模型
微分方程为
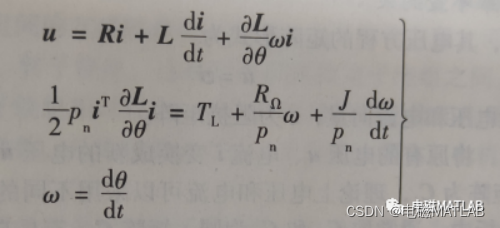
整理后为状态方程为
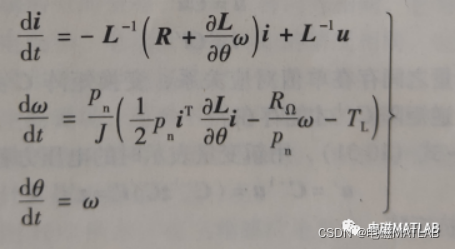
写成矩阵

即
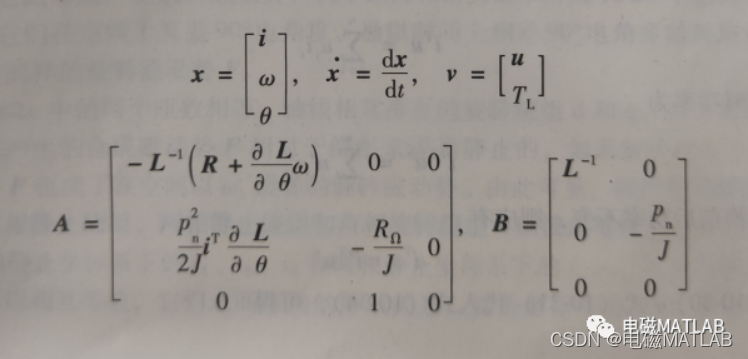
3 算例

5 matlab程序
clc
clear
close all
f=50;
Un=220;
Rs=2.68;
Rr=2.85;
LAA=0.265;
Laa=0.265;
Lms=0.253;
M12=-Lms/2;
pn=2;
J=0.02;
Romega=0;
TL=0;
%% 设置参数
y0=zeros(8,1);
TF=0.2;
options=odeset('RelTol',1e-3,'AbsTol',1e-4,'MaxStep',1e-3);
%% 调用ode45
[T,Y]=ode45(@IM,[0,TF],y0,options,f,Un,Rs,Rr,LAA,Laa,Lms,M12,pn,J,Romega,TL);
%% 计算电磁转矩
ANG=2*pi/3;
Te=zeros(length(T),1);
for k=1:1:length(T)
Theta=Y(k,8);
i=Y(k,1:6)';
DL_Theta=Lms*[0,0,0,-sin(Theta),-sin(Theta+ANG),-sin(Theta-ANG);
0,0,0,-sin(Theta-ANG),-sin(Theta),-sin(Theta+ANG);
0,0,0,-sin(Theta+ANG),-sin(Theta-ANG),-sin(Theta);
-sin(Theta),-sin(Theta-ANG),-sin(Theta+ANG),0,0,0;
-sin(Theta+ANG),-sin(Theta),-sin(Theta-ANG),0,0,0;
-sin(Theta-ANG),-sin(Theta+ANG),-sin(Theta),0,0,0];
Te(k)=0.5*pn*i'*DL_Theta*i;
end
%% 输出数据
iA=Y(:,1);
Omega=Y(:,7);
n=Omega/pn*60/2/pi;
%% 画图
figure
plot(T,n)
xlabel('时间(s)')
ylabel('nr')
title('转速曲线')
figure
plot(T,Te)
xlabel('时间(s)')
ylabel('Te')
title('转矩曲线')
。。。。。。。略