研究分类型自变量对数值型因变量的影响。检验统计的设定和检验方法与变量间的方差是否相等有关。

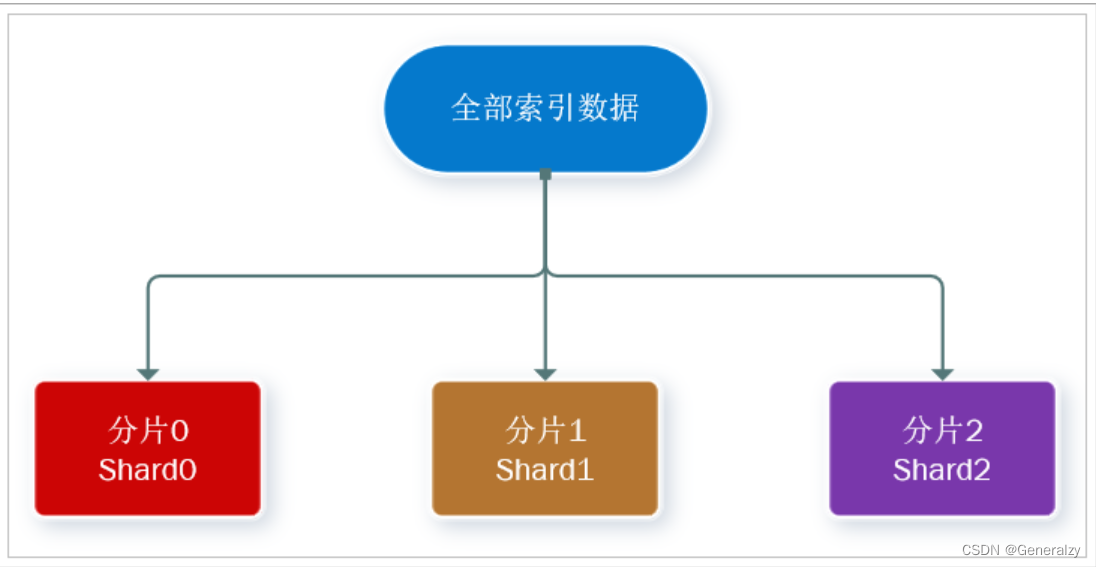
例如研究行业、服务等级对投诉数的影响：如表格中给出4个行业、每个行业有3个服务等级、样本容量为7、观测值为投诉数。则构成一个3维的矩阵。

在上述基础上，提出几个定义：

因素：行业（电网客服、电信公司客服等）、服务等级（上中下），他们都是分类变量。

水平：一个因素下有多少个分类。如服务等级这一因素有3个水平（上中下）。

因变量：受到的投诉数。

检验统计量：选择t统计量作为检验统计了，具体请自行查阅资料。

验后多重比较：检验完分类自变量对数值因变量是否有影响后，比较因素的方差。使用LSD方法，类似于双变量检验。

LSD方法：最小显著性差异法，用T检验完成各组间的配对比较，检验的敏感性比较高。

原理

条件：总体服从正态分布。同一因素不同水平之间相互独立。

ANOVA的思路为：

一个因素不同水平下的差距主要来自于抽样时的随机误差，和不同水平固有的系统误差。（合称组间误差）

同一因素的同一水平下个案的差距主要来自于抽取的随机误差（合称组内误差）

故若判断差距的主要来源为系统固有误差，则认定该分类变量对因变量有显著影响。

检验统计量F

F = 组间均方/组内均方

若F>1，则说明影响因素来自于系统误差，若<1，则说明随机误差影响比较大。

单因素方差分析

若给定4个行业，观测值为投诉数，每个行业下样本容量不唯一。

原假设：投诉数与行业有关。

检验统计量为：F，设定为与组间偏差与组内偏差有关，可自行查阅资料。

在spss打开数据文件one_waynaova1.sav  下载地址：https://download.csdn.net/download/weixin_42141390/11701140；路径为：.\10

在比较均值、单变量ANOVA操作：

4

结果为：

1、方差齐性检验表

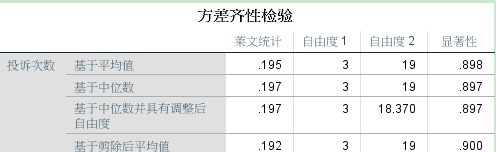
以平均值为基础，方差齐性检验的检验统计量levene F的显著水平为0.898，大于0.05，故接受原假设，即满足方差齐性。

即认为，不同行业（水平）的投诉数来自方差相等的总体。

2、单因素方差分析表：

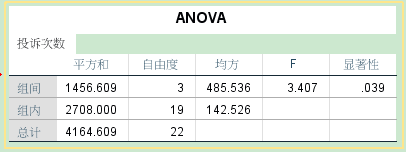
从ANOVA方差分析表中可以看出，检验统计量F的显著水平为0.04，小于0.05，故拒绝原假设，即投诉数与行业类型有关。

PS:

组间平方和为：每一组（水平）的平均投诉数与4个组的总平均投诉数之差的平方的和。

组内平方和是：20个变量于其所属水平的平均投诉数之差的平方和

均分是平方和除以自由度。

下面为验后多重比较（两两比较。）

上表为行业两两均值分析。

从表中可以看出：行业3与行业4的投诉数的均值具有显著差异。