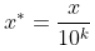有关深度前馈网络的部分知识，我们已经在吴恩达的机器学习课程中有过了解了，本章主要是对《深度学习》花书中第六章：深度前馈网络的总结笔记。我希望你在看到这一章的时候，能回忆起机器学习课程中的一些环节或者细节，这对理解本文很有帮助。

参考笔记：
前馈神经网络初探——深度学习花书第六章（一）
神经网络损失函数、输出层、隐藏层详解——深度学习第六章（二）
反向传播算法——深度学习第六章（三）
(逮住大佬的文章使劲薅）

---

---

认识深度前馈网络

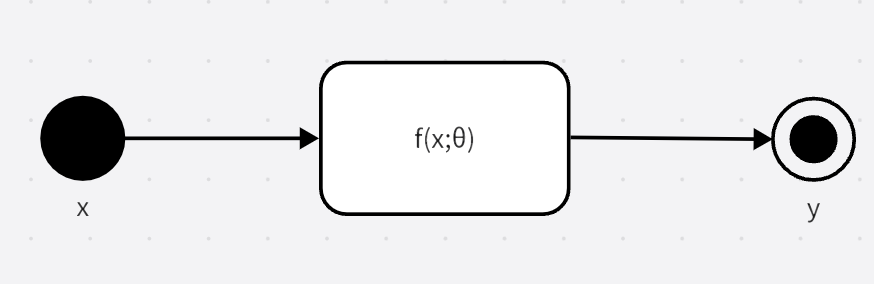
深度前馈网络，也叫前馈神经网络或者多层感知机，这是一种典型的深度学习模型，其目的是为了近似某个函数$f^{\ast }$,函数$f^{\ast }$被我们称为近似原函数$f$的一个拟合函数。我们想要得到这个函数$f^{\ast }(x)$,使得我们输入$x$能够得到近似结果$y=f^{\ast }(x)\approx f(x)$。整个神经网络相当于一个映射$y=f(x;\theta )$

像这样，信息流为$x$，过定义$f$的中间计算过程，最后达到输出$y$,在模型的输出和模型本身没有反馈连接（即输出结果作为下次输入），存在反馈连接的被我们称为循环神经网络。

假设一个神经网络函数被描述为$f(x)=f^{(3)}(f^{(2)}(f^1(x)))$，其中$f^{(1)}$被称为第一层，$f^{(2)}$被称为第二层，以此类推。链的全长称为模型的深度，前馈网络的最后一层被称为输出层，第一层被称为输入层。整个神经网络的目的是想要使$y$能够匹配$f^{\ast }(x)$的值，但是训练数据并不能告诉我们其他层该怎么做，而应该让学习算法来决定如何使用中间层来很好地近似$f^{\ast }(X)$,由于训练数据并未给出中间层所需的输出，因此我们把中间的那些层称为隐藏层。

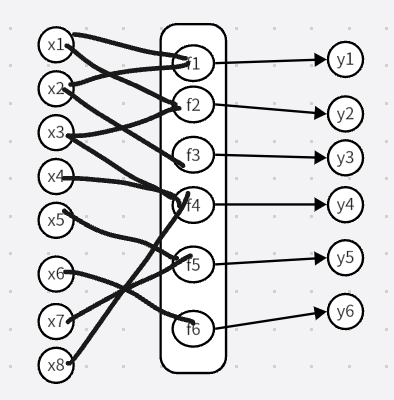
神经网络中的每个隐藏层通常都是向量值，这些隐藏层的维度决定了模型的宽度。我们最好把每层隐藏层想象成许多并行处理的单元，每个单元表示一个处理x个向量成为一个标量的函数。每个单元类似于神经元，它接受来自其他多个单元的输入并计算它自己的激活值，每个神经元进行了矢量到标量的映射操作（这一操作又被称作激活函数，activation function），而每一层是不同的神经元并行运算的综合。

偏爱线性模型

建立深度前馈网络的一个考虑是从线性模型开始，并设法克服它的局限性，例如线性回归和逻辑回归，它们无论是通过闭解形式还是使用凸优化，都能高效且可靠地拟合。但是线性模型也有明显的缺陷，那就是模型的能力被局限于线性函数，它无法理解任何两个输入变量间的相互作用。

• 为了拓展线性模型来表示x的非线性函数，我们可以不把线性模型应用于x本身，而是用于一个变换后的输入$\varphi (x)$上，$\varphi$指的是一个非线性的变换，这种方法将线性模型拓展为非线性模型，并利用线性模型的性质来解决。
• 如果你还记得我们讲过的核函数，我们也可以隐含地使用$\varphi$映射的非线性学习算法，将一个非线性问题转化为一个线性问题再解决。

$\varphi$可以简单地理解为对原函数$f(x)$或者对x内所隐含特征的映射。

1. 对于如何选取映射 $\varphi$有如下几种思路：选取一个比较通用的 $\varphi$，例如核技巧中的RBF kernel（也称作Gaussian kernel），如果$\varphi (x)$的维度足够高，我们总能够使其匹配训练集，但很难推广到测试集。因为这种模型只是假设了局域变化不大的前提，而并没有包含任何有价值的先验信息。
2. 人工选取合适的 $\varphi$，实际上这是在深度学习流行之前的主流方法，但是这需要大量的相关经验与人力资源，而且不同领域间的知识很难迁移。
3. 深度学习的策略是利用神经网络学习合适的用隐藏层代表的映射$\varphi$，即模拟$y=f(x;\theta ,w)=\varphi (x;\theta {)}^{T}w$,其中$\theta$是$\varphi$的模拟参数，我们需要从一大类函数中进行学习得到，以及用于将$\varphi$映射到所需的输出的参数$w$。这种方法可以兼具方法一二的优点，如果我们想要得到高度通用的$\varphi$，只需使用一个非常广泛的函数族（函数集合)$\varphi (x;\theta )$来训练参数$\theta$
   我们也可以人为的设置表现优异的函数族$\varphi (x;\theta )$重新训练，与第二种方法相比，优点在于我们只需找到一个比较合适的函数族而不需要知道确切的函数。

第三种方法可以对应我们之前学到的：预训练可以在不同功能的同一模型内迁移参数并微调。并且这个方法不仅适用于深度前馈网络，甚至可适用所有种类的深度学习模型（指的是同一种模型内迁移参数都适用）。

实例：学习XOR

XOR指的是异或函数，对于两个二进制输入$x_1,x_2$（即输入结果只有0和1），若有且仅有一个输入为1则输出1，反之其余情况都输出0，如下图所示：

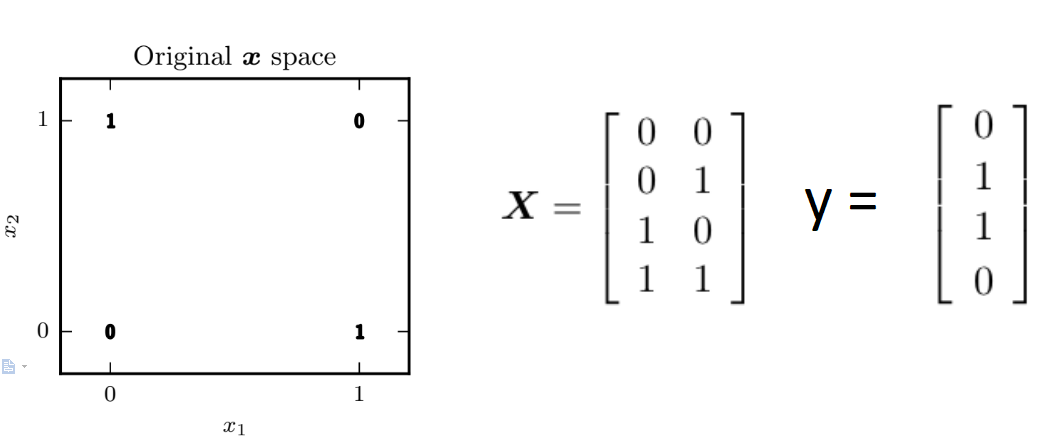
由于它的输出只有这四个，因此我们要用这四个样本来训练我们的网络。

很明显，我们无法对当前的向量空间进行线性分割，使得两种的输出结果被分别分割到线性函数的两侧。

当然书上给出了一个证明过程:假设线性回归模型$f(x;w,b)=x^{T}w+b$
其MSE(均方误差)代价函数为:$J(\theta )=\frac{1}{4}\sum _{x\in \mathbb{X}}(f^{\ast }(x)-f(x;\theta ){)}^2$（线性回归的代价函数基本都是均方误差）

运用梯度下降或者正规方程，我们找到使得$min(MSE)$的参数$\theta 或者说(w,b)$，我们得到$w=0$,$b=\frac{1}{2}$,意味着$f(x;w,b)=0.5$在任意点都是这个输出，和我们的结果不能说没有关系，只能说八竿子打不到一块。也就证明了一个我们一眼就看出来的结论：线性回归不适合拟合这个模型。

这种时候想想核技巧会怎么做，其中一个方法就是：使用一个模型将其映射到一个新的特征空间，在这个特征空间内，我们可以用线性模型来解决。

我们引入一个如下图所示的简单的具有一层隐藏层的前馈网络模型：

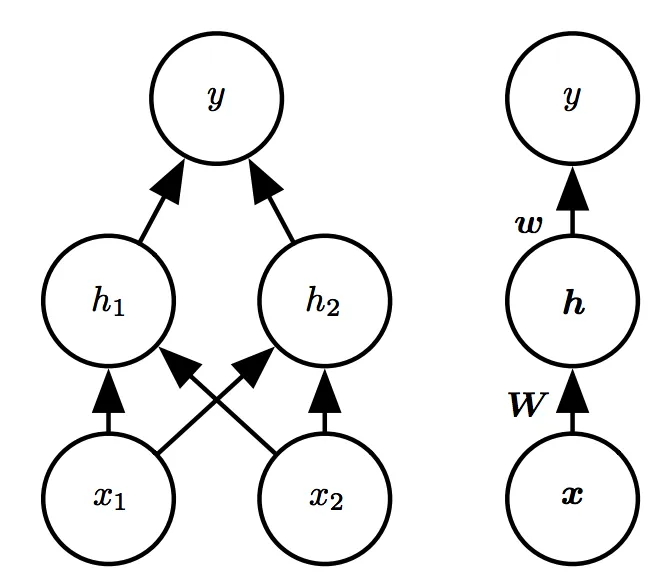
注意图中两种方式表示是等价的，左图是具体画出每个节点，而右图是简化为层。并且用$W\&w$来表示了不同层次间的映射关系。

这个简单的神经网络甚至简单到只有两层，$x$层不在神经网络内，它代表的是输入特征，$h$层是神经网络的第一层隐藏层，也是输入层，$y$层是第二层，但不是隐藏层，是输出层。

在上述模型中包含了两个函数$h=f^{(1)}(x;W,c)$和$y=f^{(2)}(h;w,b)，$完整的模型是$f(x:W,c,w,b)=f^{(2)}(f^{(1)}(x))$，如果详细地展开整个映射：
$h1=W_{11}\ast x1+W_{21}\ast x2+b_{11}；$
$h2=W_{12}\ast x1+W_{22}\ast x2+b_{12}；$
$y=w_{11}\ast x1+w_{21}\ast x2+b_{21}$，
其中$W_{11}$代表第1层从$x_1,x_2\to h_1$的参数$W$,$b_{21}$代表第2层第1个神经元的常数参数，以此类推。

好处之一就是我们现在构建这个模型不用知道具体函数，只需要写出函数族即可，所以我们可以简单地把神经网络的层次先建立起来。现在让我们思考应该选择哪个函数来表示$f^{(1)}$?似乎线性函数可以，遗憾的是线性函数的线性函数，也就是$F(x)=f(f(x))$，若$f(x)$是线性函数,则$F(x)$也是线性函数，证明略，自己代入可证。因此我们肯定不能选择线性函数了。

当然，我们学习过神经网络了，知道现在我们应该采用一些非线性的激活函数来实现这个目的，现在我们需要一个偏置参数$W^T$来描述从$\vec{x}\to \vec{h}$的仿射变换，我们需要一整个向量的偏置参数，因此激活函数$g$通常需要选择对每个元素$x_i$分别起作用的函数，从而有$h_i=g(x^{T}W;i+c_i)$。在现代神经网络中，我们默认的推荐是ReLu函数 g ( z ) = m a x { 0 , z } g(z)=max\{{0,z}\} g(z)=max{0,z}

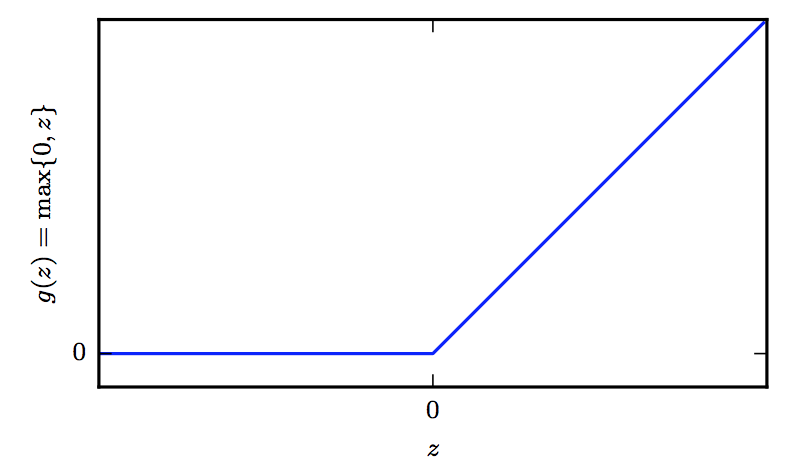
(整流线性激活函数ReLu非常接近线性，本质上它是具有两个线性部分的分段线性函数，ReLu几乎是线性的，因此保留了线性模型能够泛化良好的属性。就像计算机一样，我们可以从0和1构建一个复杂的系统，因此我们也可以通过整流线性函数构建一个万能函数近似器）

因此我们带入$f^{(1)}=g(z)$，得到完整模型 f ( x ; W , c , w , b ) = w T   m a x { 0 , W T x + c } + b f(x;W,c,w,b)=w^T\space max\{{0,W^Tx+c}\}+b f(x;W,c,w,b)=wT max{0,WTx+c}+b

那么我们开始训练数据了，按照真值表的输出，我们需要使得模型拟合下面的训练样本：

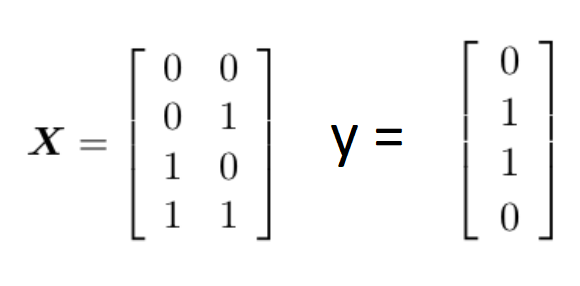
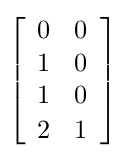
那么我们可以找到一个解：

此时b=0，将训练集带入验证，
在第一层中，我们用输入矩阵 $X$*权重矩阵$W$,得到$XW=\left[\begin{array}{cc}0& 0\\ 1& 1\\ 1& 1\\ 2& 2\end{array}\right]$,再加上偏置向量$c$得到$XW+c^T=\left[\begin{array}{cc}0& -1\\ 1& 0\\ 1& 0\\ 2& 1\end{array}\right]$，这是由输入层到ReLu的映射，接下来我们用ReLu对每个样本进行处理，得到隐藏层的输出值：

我们说这是非线性模型到线性模型的拓展，这个输出值从原空间通过映射$\varphi$到隐藏层的特征空间$h$，在特征空间上我们可以用线性模型来解决。

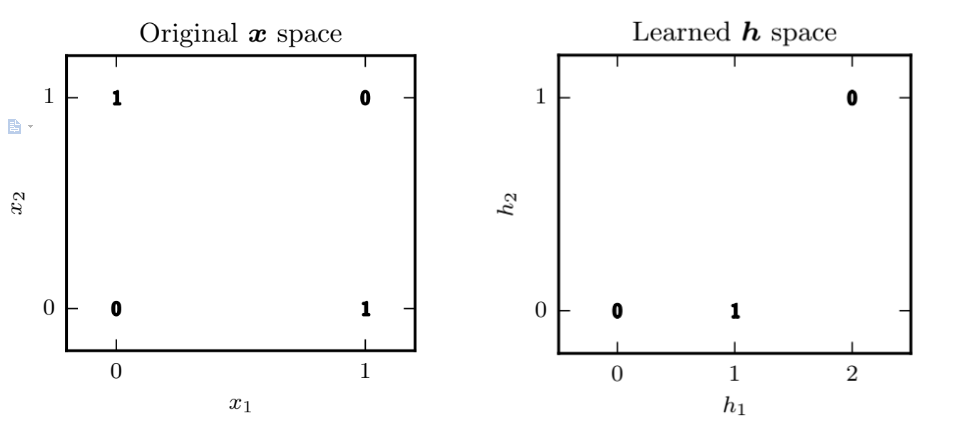
(左图是原空间，右图就是特征空间$h$,与原空间相比，$h$将$x=[1,0{]}^T和x=[0,1{]}^T$这两个点映射到了$h=[1,0{]}^T$，使得原来无法用线性模型拓展的原空间为了可以可以使用线性模型的特征空间)
最后乘以权重向量$w=\left[\begin{array}{c}1\\ -2\end{array}\right]$,$(XW+c^T)w+b=\left[\begin{array}{c}0\\ 1\\ 1\\ 0\end{array}\right]$

这个例子中，我们用简单的神经网络并找到合适的解来模拟XOR操作，实际中问题要复杂得多，而我们不能这么容易的猜到合适的解，这时候我们就需要利用梯度下降算法来逼近合适的解。下一篇继续总结利用梯度下降算法的前馈神经网络模型的基本组成包含模型的损失函数，输出层函数，隐藏层函数以及整体架构的选择。