安装 scikit-learn
术语理解
- 1. 特征（feature ）和样本（ sample / demo）的区别？
- 2. 关于模型的概念
一、机械学习概念
- 1. 监督学习
- 总结：
- 2. 非监督学习
- 总结：
- 3. 强化学习
- 总结：
- 三种学习的特点总结
- scikit-learn 说明
二、机械学习的基本实操逻辑
- 1. 采集数据
- 2. 数据预处理(Preprocessing)
- - 预处理算法：
  - - 归一化：
    - - 1.normalize()
- 3. 数据降维处理 (Dimensionality reduction)
- 4. 分类(Classification)、回归(Regression)、聚类(Clustering)处理三选一
- 5. 模型选择 (Model selection)
三、数据预处理 —— 数据分析
- 数据规范化详解 —— 归一化 / 标准化
- 如何区分归一化和标准化
- - 数据归一化 —— 范围缩放(scale)及映射
  - 1. 最大最小规范化(归一化)(Min-Max Normalization) [0,1] / 范围缩放（Scaling）
  - - 功能：
  - 2. Mean normalization (均值归一化)[-1,1]：
  - 前两种归一化方法应用场景：
  - 前两种归一化方法不适用场景：
  - 3. 小数定标规范化(归一化) （normalization by decimal scaling）
  - - 功能：
  - 什么时候用归一化？
  - 数据标准化 std
  - 1. 零-均值规范化 (标准化)（z-score standardization）/ 均值移除(Mean removal)
  - - 功能：
    - 意义：
    - 应用场景：
  - 什么时候用标准化？
归一化与标准化资料链接：
下一章节跳转链接

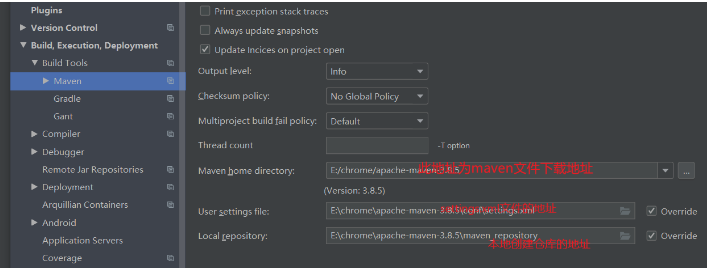
安装 scikit-learn

记得在虚拟环境下安装，这里推荐 Virtualenv

pip install scikit-learn

链接：Windows 10 - Python 的虚拟环境 Virtualenv - 全局 python 环境切换问题

在这里 scikit-learn框架的核心模块 —— sklearn，而不是 scikit

import sklearn

测试环境：（请注意这里是虚拟环境 Virtualenv）

操作系统： Window 10
工具：Pycharm
Python: 3.7
scikit-learn: 1.0.2
numpy: 1.21.6
scipy: 1.7.3
threadpoolctl: 3.1.0
joblib: 1.1.0

术语理解

1. 特征（feature ）和样本（ sample / demo）的区别？

一个样本由多个特征组成，而特征是一个样本的元素；
对于数据的处理，通过设置轴参数axis 为 0 或 1 ，可以选择对样本们，进行特征向量运算(纵向)或样本特征运算(横向)；
样本指横向的元素，特征指纵向的元素。这句话的意思是，当你设置axis = 0 或 axis = 1时，那么当为 0 时，指向纵向的特征元素，为 1 时，则指向横向的样本元素，举个例子，假如有样本 A 和样本 B，其中样本 A 和样本 B 都有特征 a、b、c ，那么当axis = 0 时，则按顺序取样本 A 和样本 B 的特征 [Aa, Ba]，[Ab, Bb]，[Ac, Bc]，当 axis = 1 时，则按顺序取样本 A 的特征 [Aa, Ab, Ac] ，然后再取样本 B 的 [Ba, Bb, Bc]

具体演示：

0|1		  	a   	b		c   
样本 A		Aa		Ab		Ac
样本 B		Ba		Bb		Bc

某个矩阵内的所有的输入值 x ,最终经过算法转换，得到输出值特征 y

2. 关于模型的概念

所谓的机器学习模型，本质上是一个函数，其作用是实现从一个样本 $X$ 到样本的标记值 $\rightarrow x$ 的映射
通俗概括：可以从数据中学习到的，可以实现特定功能（映射）的函数。
进一步专业性概括：模型是在指定的假设空间中，确定学习策略，通过优化算法去学习到的由输入到输出的映射。

现实中，我们可以看到一些用塑料制造出来的人物、机器等模型，这就是相当于一个映射，从脑海里的想法 x 中，映射为塑料模型 y ，还有3D模型，也是同理，通过构建模型 y，映射出脑海里的 x ，但是机械学习的模型，也是一样的吗？
那是自然，通过已知的数据 x 映射出未知的数据 y，来构建出一个预测模型，该模型是通过监督、非监督、强化等学习策略，以算法为工具，来构建一个模型。

实际理解：编程语言的函数 $f (x)$ ，输入矩阵 $X$ ，也就是样本 $X$ ，返回值是一个模型对样本的转换后的映射 $Y$ ， $Y$ 是一个预测值。

一、机械学习概念

机械学习共分为三种学习：

监督学习
非监督学习
强化学习

1. 监督学习

监督学习（Supervised Learning）的任务是学习一个模型，使模型能够对任意给定的输入，对其相应的输出做出一个好的预测。
即：利用训练数据集学习一个模型，再用模型对测试样本集进行预测。

通俗理解：每个数据点都被标记或关联一个类别或者分值。

例（类别）：输入一张图片，判断该图片中的动物是猫还是狗；

例（分值）：通过大量数据预测一辆二手车的出售价格；

监督学习的目的就是学习大量的样本（称作训练数据），从而对未来的数据点做出预测（称作测试数据）。

分类和回归，从根本上来说，分类是预测一个标签，回归是预测一个数量。

分类是给一个样本预测离散型类别标签的问题。

回归是给一个样本预测连续输出量的问题。

这段引用，笔者个人理解是，模型是具备输入值和输出值的，即 $X$ 和 $Y$ ，当统计完这个模型内的一般规律，就可以用这个统计出来的一般规律，来预测其他的输入值 $X$ 的可能性，即输出值 $Y$ ，当然这一点，其实就很麻烦，现实世界可无法仅仅通过一个模型的规律，就能预测的了结果，所以只能说模型多多益善。

对于分类，笔者认为是点状预测，一个点一个点的预测出来，而不是像一条线那样；
回归则是线性预测，例如可以预测股票的线性变化，笔者个人大致是这样认为的。

总结：

监督学习，需要人去找模型去喂给它，还要多多观察该模型的准确性，也就是要监督并观察该算法的性能及准确度，就好比如有的小孩子需要我们大人去监督它们的学习，这样它们会在我们的监督下，认真学习，并提高成绩，这里指的是提升算法的性能和模型的准确度。
所以哪些需要模型的，都是监督学习。

2. 非监督学习

非监督学习（Unsupervised Learning）为直接对数据进行建模。没有给定事先标记过的训练范例，所用的数据没有属性或标签这一概念。事先不知道输入数据对应的输出结果是什么。

自动对输入的资料进行分类或分群，以寻找数据的模型和规律。

例：聚类

总结：

非监督学习，孩子需要靠自己自学成才，不应该需要我们去监督它们学习，这样才能独立自主，由于现实生活中的变化，我们不太可能拥有全部的现实模型，在某种情况下，我们不太可能一直监督它们学习，所以需要它拥有自学的能力，通过自主收集现实的样本特征，自动的对自己进行变量输入，从而获取一个又一个的模型，然后对于模型进行一个性能或准确度的评估等等。

3. 强化学习

强化学习（Reinforcement Learning）是机器学习中的一个领域，强调如何基于环境而行动，以取得最大化的预期利益。其灵感来源于心理学中的行为主义理论，即有机体如何在环境给予的奖励或惩罚的刺激下，逐步形成对刺激的预期，产生能获得最大利益的习惯性行为。

总结：

强化学习，孩子在学会了自主学习后，对它们进行一个激励的学习奖励措施，那么其会有可能形成一个应激性的行为，然后孩子就会容易去做某种对自己有利的事，比如设计一个撞墙的强化学习算法，那么对于撞墙就会执行一个闪避的有利选择，所以我们可以利用这一点，设计出一个符合该设想的机器学习算法，即强化学习。

三种学习的特点总结

有监督学习、无监督学习、强化学习具有不同的特点：

监督学习是有一个label（标记）的，这个label告诉算法什么样的输入对应着什么样的输出，常见的算法是分类、回归等；
无监督学习则是没有label（标记），常见的算法是聚类；
强化学习强调如何基于环境而行动，以取得最大化的预期利益。

scikit-learn 说明

scikit-learn库主要功能分六大部分：分类，回归，聚类，降维，模型选择，数据预处理

分类、回归 ——> 监督学习
聚类 ——> 非监督学习

二、机械学习的基本实操逻辑

1. 采集数据

这里先不介绍采集数据，笔者还没涉猎。

2. 数据预处理(Preprocessing)

在真实的世界中，经常需要处理大量的原始数据，这些原始数据是机器学习算法无法理解的，为了让机器学习算法理解原始数据，需要对数据进行预处理。

所谓的预处理，也叫规范化，其实就是提取复杂数据里的有价值的内容，这里用到了归一化或标准化：

数据归一化/标准化 —— 将原始数据分为训练用数据和测试数据，测试数据是从原始数据中抽出一部分充当测试用的数据（这在监督学习中很常见）

预处理算法：

归一化：

1.normalize()

3. 数据降维处理 (Dimensionality reduction)

通常而言，做机器学习时，你的数据量越大，维度越多，考虑的因素越多，你的分类、回归的预测就会越准确，但也因为是考虑的太多了，你的计算也就会越慢，所以在这里就会考虑要怎么权衡预测的准确度和计算速度。
在保证最大信息量的情况下，减少维度，降低计算的时间。

减少维度，可以更好的可视化，超过了三维，人就会难以理解，所以降维可以将数据更好的可视化，还有提升计算的效率(机器学习最根本的一点)

降维算法：

4. 分类(Classification)、回归(Regression)、聚类(Clustering)处理三选一

分类算法：

回归算法：

聚类算法：

5. 模型选择 (Model selection)

三、数据预处理 —— 数据分析

数据规范化详解 —— 归一化 / 标准化

数据规范化处理是数据挖掘的一项基础工作。不同评价指标往往具有不同的量纲，数值见的差别可能很大，不进行处理可能会影响到数据分析的结果。为了消除指标之间的量纲（不同的物理量）和取值范围差异的影响，需要进行标准化处理(对数据进行预处理)，将数据按照比例进行缩放(归一化处理)，使之落入一个特定的区域，便于进行综合分析。如将工资收入属性值映射到 $[- 1, 1]$ 或者 $[0, 1]$ 内（这是归一化例子）

数据规范化对于基于距离的挖掘算法尤为重要。（这里的基于距离指的是变量输出值之间的距离）

规范化指归一化或标准化

如何区分归一化和标准化

归一化和标准化都是对数据做变换的方式，将原始的一列数据转换到某个范围，或者某种形态，具体的：

归一化(Normalization)：数据归一化用于需要对特征向量的值进行调整时，以保证每个特征向量的值都缩放到相同的数值范围，将一列数据变化到某个固定区间(范围)中，通常，这个区间是 $[0, 1]$ ，广义的讲，可以是各种区间，比如映射到 $[0, 1]$ 一样可以继续映射到其他范围，图像中可能会映射到 $[0, 255]$ ，其他情况可能映射到 $[- 1, 1]$ ；
标准化(Standardization)：将数据变换为均值为0，标准差为1的分布 $[0, 1]$ ，切记，并非一定是正态的；
中心化：另外，还有一种处理叫做中心化，也叫零均值处理，就是将每个原始数据减去这些数据的均值。(其实也就是上面的标准化)

有时候会看到标准归一化，其实也差不多，说是标准化，其实这个定义早就被归一化的概念给覆盖了，标准化归一化都可以这么叫，但是具体到它们的实现公式就得考虑清楚，名字随意，实现它们时，就得看看是怎么个处理方法。
一个是等比例缩放、一个是去均值中心化缩放。

数据归一化 —— 范围缩放(scale)及映射

scale n. 天平，磅秤；；刻度，标度；标尺，刻度尺；v 缩放

广义的说，标准化和归一化同为对数据的线性变化，所以我们没必要规定死，归一化难道就必须到 $[0, 1]$ 之间，我到 $[0, 1]$ 之间后，然后再乘一个255，你奈我何？所以切记不要被概念所束缚住，常见的有以下几种：

1. 最大最小规范化(归一化)(Min-Max Normalization) [0,1] / 范围缩放（Scaling）

功能：

归一化的最通用模式Normalization，也称线性归一化、最小-最大规范化，也称为离散标准化，是对原始数据的线性变换，将数据值映射到 $[0, 1]$ 之间

转换公式如下：

$X_{new}=\frac{X_{i}-X_{min}}{X_{max}-X_{min}}$ ，范围 $[0, 1]$

$X_{i}$ : 指的是要归一化的数据，通常是二维矩阵
$X_{max}$ : 每列中的最大值组成的行向量
$X_{min}$ : 每列中的最小值组成的行向量
$X_{new}$ : 指的是占比结果，到了这一步其实还不算完整，看下面的公式中的 $X_{scaled}$

或

$X_{std}=\frac{X_{}-X_{.}min(axis=0)}{X_{.}max(axis=0)-X_{.}min(axis=0)}$

$X_{scaled}=X_{std}\times(max-min)+min$ ，范围 $[0, 1]$

乍看一下很懵逼，解释一下：

$X$ :要归一化的数据，通常是二维矩阵，例如

[[4,2,3]
[1,5,6]]

$X . min (a x i s = 0)$ ：每列中的最小值组成的行向量，如上面的例子中应该是[1,2,3]
$X . ma x (a x i s = 0)$ ：每列中的最大值组成的行向量，如上面的例子中应该是[4,5,6]
$ma x$ : 要映射到的区间最大值，默认是1 ，可以根据情况更改，不要被束缚住
$min$ ：要映射到的区间最小值，默认是0 ，可以根据情况更改，不要被束缚住
$X_{std}$ : 占比结果
$X_{scaled}$ : 最终的归一化结果，映射到范围 $[0, 1]$ 而已，借助 $X_{std}$ 完成最后一步的 $X_{scaled}$ ， $min$ 为 0.

再用朴实的语言描述一下上面公式所做的事：

第一步求每个列中元素到最小值距离占该列最大值和最小值距离的比例，这实际上已经是将数据放缩到了 $[0, 1]$ 区间上
第二步将占比结果数据按同等比例缩放映射到指定的 $[min, ma x]$ 区间

2. Mean normalization (均值归一化)[-1,1]：

若要转换到 $[- 1, 1]$ 之间，则

$X_{std}=\frac{X-X_{mean}}{X_{max}-X_{min}}$
$X_{scaled}=X_{std}\times(max-min)+min$ ，范围 $[- 1, 1]$

$X_{std}$ : 去除均值的占比结果
$X_{mean}$ 代表了 $X$ 的每一列的均值
$X . min (a x i s = 0)$ ：每列中的最小值组成的行向量
$X . ma x (a x i s = 0)$ ：每列中的最大值组成的行向量
$X_{scaled}$ : 最终的归一化结果，所谓的映射，本质是放大了 $X_{std}$ 的数值，映射到范围 $[- 1, 1]$ 而已
$ma x$ : 要映射到的区间最大值，默认是1 ，可以根据情况更改，不要被束缚住
$min$ ：要映射到的区间最小值，默认是0 ，可以根据情况更改，不要被束缚住

前两种归一化方法应用场景：

在不涉及距离度量、协方差计算、数据不符合正太分布的时候，可以使用该方法或其他归一化方法（不包括Z-score方法）。比如图像处理中，将RGB图像转换为灰度图像后将其值限定在 $[0 - 255]$ 的范围

前两种归一化方法不适用场景：

原始数据存在小部分很大或很小的数据时，会造成大部分数据规范化后接近于 0 或 1，区分度不大，比如 ( 1， 1.2， 1.3， 1.4， 1.5， 1.6，8.4）这组数据。若将来遇到超过目前属性[min, max]取值范围的时候，会引起系统报错，需要重新确定 $min$ 和 $ma x$ —— 将这组数据标准化(归一化)，然后得到的一组规范化后各值接近于0的数据，假如以后加入新的数据，会有可能超过该数据标准化后的最大最小的范围，就需要重新确定 $min$ 和 $ma x$

3. 小数定标规范化(归一化) （normalization by decimal scaling）

功能：

通过移动属性值的小数位数，将属性值映射到[-1, 1]之间，移动的小数位数取决于属性值绝对值的最大值。

转化公式为： 原始值 / 10^k
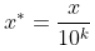
在这里插入图片描述
$X_{new}=\frac{X}{10^k}$

k 取决于 $X$ 内的属性取值中的最大绝对值
小数定标规范化就是通过移动小数点的位置来进行规范化。
小数点移动多少位取决于 $X$ 内的属性的取值中的最大绝对值。

这里的 $X$ 内的属性代指样本实例的某种属性，比如长度、宽度、数量等。
也就是说找的是矩阵内绝对值化后的最大的输入值元素x，并且使用恰当的对数函数方法 log10 ，以10为底，值为该绝对值化的最大值 max(x) ，即 $log_{10} max(X) = k$ ，得到 k 值，还要注意的一点是 $k$ 值必须是向上取整，这里提供一个方法是numpy模块的 ceil(k)方法，向上取整方法，注意不是四舍五入，而是整个小数点后的值都被舍去了。完整公式： $X_{new} = ceil(log_{10} max(abs(X)))$ ，abs() 是绝对值函数