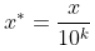本章是比较独特的一章,相对于前面的内容,内容较为独立,主要描述的是力学相关的一些理论。因此,读者也完全不必根据题目产生一些不必要的幻想,认为似乎看完这章我就可以学会机器人抓取。
不过,我仍然认为这章的内容是好的,且是必要的,因为实践的内容做的多了,往往就麻木了,纯粹变成一个工具人了,而不去思考背后深刻的原因。本章以可视化分析的形式,分析了接触运动学与接触力学的一些理论知识,非常有趣,建议阅读。
ps:年后的工作一下子忙了许多,每天就面向业务在做一些很繁琐的事情。静下心来想一想,每天忙忙碌碌,只有产出,却没有提升。回到家总是筋疲力尽,以至于根本没有精力去打开电脑,自己学习提升。
希望这种状态是短暂的吧。
接触运动学
令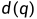 为两个刚体之间的距离,q为两个刚体的位形,
为两个刚体之间的距离,q为两个刚体的位形, 为距离关于位形的导数,
为距离关于位形的导数,
那么显而易见, 时两刚体保持接触,并且
时两刚体保持接触,并且 是刚体接触的必要条件。
是刚体接触的必要条件。
(dq>0时为分离,<0时为穿透)
而不可穿透约束则可以写为:

可以看出如果物体A的接触点以及物体B的接触点的速度如果相同,或者虽然不同但是它俩和接触法线垂直,则保持接触,即 ,如果大于等于0则未接触。
,如果大于等于0则未接触。
当然,根据本书的惯例,一切都要表示成旋量的形式,参考最开始刚体运动这节课:
【现代机器人学】学习笔记二:刚体运动
我们知道旋量中的线速度v是沿轴的速度v与沿轴旋转引起的速度,即

移项推导,最后引入力旋量,得到新的不可穿透约束:

另外对于接触状态,还定义了有效约束:(注意书中印刷错了)

满足有效约束的运动旋量VA和VB称为 一阶滚动-滑动运动。
这里区分滚动和滑动:
滚动约束:

即两个接触点的速度在某个坐标系下保持一致,那么这个接触叫做“滚动”rolling contact。
滑动:
满足有效约束,但是不满足滚动约束的,称为滑动约束。
用人话来说,就是两个物体的接触点是变化的,但是他们变化的方向和接触的法向量是垂直的,好比你穿上了时尚的滑板鞋,在这光滑的地上摩擦,鞋子并未脱离地面,所以鞋子和地面就是滑动。但是你的脚带着鞋一起动,脚底板和鞋垫之间就算是滚动摩擦。
多刚体接触
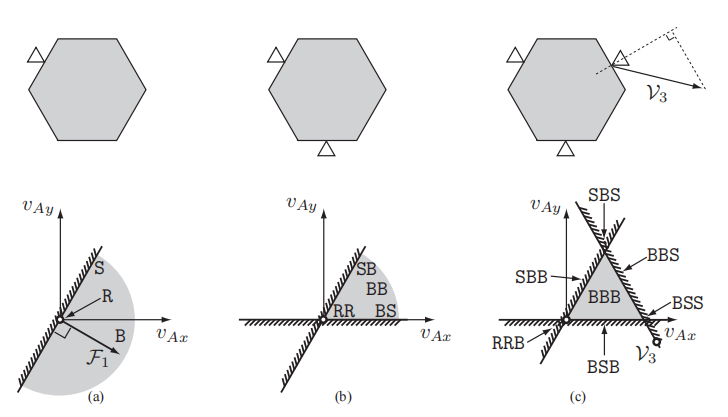
B表示脱离,S表示滑动,R表示滚动接触。
图a里,左上有一个手指。S那个面上属于滑动,因为可以顺着它滑。R的那一个点,算是滚动接触。而B整个区域则是脱离的接触。
图b中,也可以同样的分析,可以看到图中字母变成了两个,分别代表两个手指的接触状态。
图c中,假设右上方的手指在沿着V3方向移动,一共有七种可能的结果,我们可以看到,最后一个接触点不可能是R,因为如果是R的话,物块得沿着V3方向运动,那就得穿透第二个手指了,违反了不可穿透约束。
可行旋量多面体凸锥
如例题12.4,给了三个力旋量,然后给了限制即物体在平面上移动,即限制了vz,wx,wy,最后套入不可穿透约束的公式,运动约束表示为:

然后用锥体对它进行可视化:
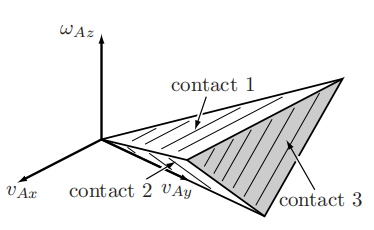
则这个锥体内部的旋量,属于脱离类型的接触。
锥体的边缘和平面上的值对应的旋量,是有效约束。(即不可穿透约束刚好等于0的情况)
注意:
对于多个接触体,复合运动旋量空间,是以原点为顶点的。(上图就是一个例子)
m个物体构成的组合中,运动旋量的空间为6m维,每个接触就对这个维度产生一个约束。接触模式则像再上方的那个abc的图一样,是每个接触点接触方式的级联。
但是如果手指是机器人手指,是受到控制的,那么这样抓握的物体的可行的旋量锥体就不一定是以原点为顶点了。
其他类型接触
之前介绍的接触,都是至少有一个物体唯一的定义了接触的法线。(即12.6 a)
但是还有一些其他类型的接触,作者罗列了出来,意味着不再是手指的一个尖触点来接触物体的面。

作者提到e是退化场景不再考虑。
平面图形化方法
这一节的内容是用来分析单个物体的可行运动的。直接啃的话,说实话看起来是有些抽象的。不过我在这里直接用简单的方法描述它,让大家减少一些阅读的痛苦:

我们用旋转中心来描述物体的旋转,其中+为右手定则,逆时针旋转,0为不转,-为顺时针旋转。
然后这个图就只是一个对可行运动旋量的一个可视化,它分布在两个平面或者中间的球上:
(我们本节的运动是平面运动,因此只有wz,vx,vy有效,其他是0)

暂停一下:我觉得读者应该清楚的认识到作者是在讲些什么内容,不应该糊里糊涂的。我觉得对读者而言,可以不理解他的细节,但是应该知道他想表达什么内容。
现在在讲的CoR的分析是用来干嘛的?
是用来表示“与静止物体相接触的可移动物体的可行运动”。
对于一个静止手指,加上一个物体,可行的运动方式为:
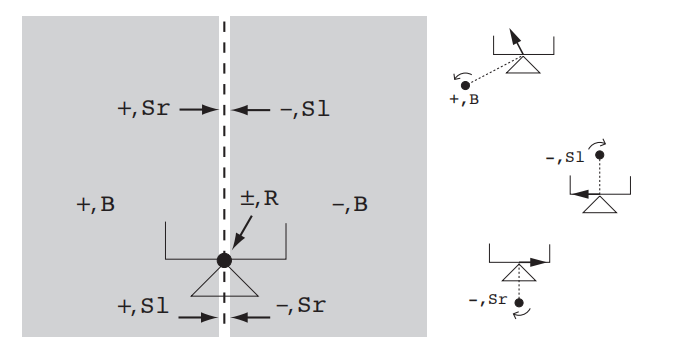
这个图看似抽象,实际还是比较简单的。Sl表示物体向左滑动,Sr表示向右滑动。图里的+,Sl表示物体在接触点这里,关于接触点一瞬间是以逆时针在转,同时有向左的滑动。。其他以此类推,读者别被这些符号吓傻了。
为什么要分析单个物体的接触?
因为分析清楚了单个物体,多个物体的接触就是各自把这些东西画出来,舍去不合理的地方。例如:
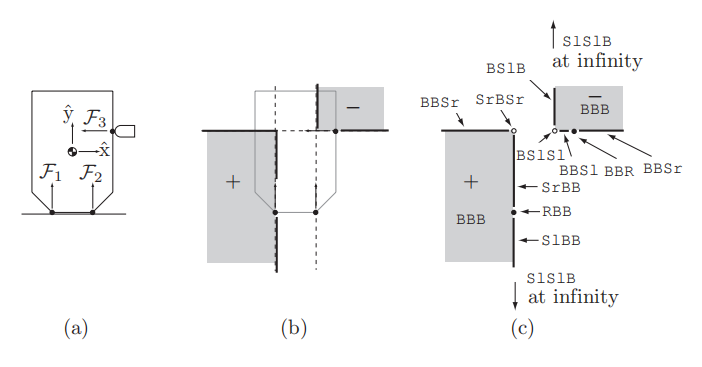
我们可以看到,F1左边是+,那么F1右边是-,但是F2左边又是+,因此这里正负就抵消掉了。所以从b图可以看出,只有灰色的区域是能转动的。那么根据c图,也类似分析,Sl和Sr抵消的内容,就可以得到一系列候选的运动方案。
但这种只是一个简单的推理,并不是保证正确的,例如+SrBSr,这种用图的方式分析出来,似乎是合理的。但是这意味着,物体在左边+的区域逆时针转,同时对F1的接触往右滑动,对F2处的接触脱离,对F3处的接触向上滑动,即保持F1和F3的接触,脱离F2的接触。这怎么可能?直观上想象一下这个运动就不可能,根本就抬不起右下角的接触,因为它会穿透F3手指。
难道我们现在的分析不对吗?作者对这种原因给出了解释:
我们是采用一阶分析。
因此,结论是,n阶的滚动-滑动运动,可能被n+1阶的分析,分析为是穿透接触或者是脱离接触。但是一旦n阶已经分析称为穿透或脱离,更高阶的分析也不会再改变结论。
形封闭
如果一组静止约束可以阻止物体的所有运动(即抓牢了),可实现物体的形封闭。
线性代数理论:
1.空间R^n最少由n个向量线性组合表示。即n个坐标表示n维欧几里德空间。
2.空间R^n最少由n+1个向量正线性组合表示。即取作为多出的一个向量,然后就可用这个多出的向量和原本的向量的正线性组合来表示空间了。
一阶形封闭需要的接触数量:
对于空间物体,需要6+1=7个接触。因为空间物体时6维,而限制了正线性组合,因为

我之所以把线性代数的引用放到这里,而不是最开始就介绍,这是因为这里才用到。哪里用到在哪里提嘛!那么对于平面物体,则需要3+1=4个接触,也是同样的原因。
当然有个特例,就是圆。不管怎么接触,它理论上讲都能转。
参见12.14图,根据+-的分析方式,三角形也能绕中心旋转。但实际上不可能。
因此结论是:
一阶形封闭 ----> 高阶形封闭
一阶滚动滑动 ------> 高阶形封闭 或 不封闭。
一阶形封闭的线性规划测试
令F作为一个列向量由j个接触力旋量组成的矩阵。
矩阵F不满秩,则不处于形封闭。
矩阵F满秩,计算Fk=0是否有正系数k>0的解,有解则形封闭,无解则不封闭。
评:这种方式跳过了画图分析,直接通过数学的方式判断是否属于一阶形封闭。
形封闭质量的度量
同样是两个抓握,哪个质量更好?这是个好问题。
我们需要定义一个抓握度量,Qual(F),当它小于0的时候抓握不是形封闭,大于0时越大抓握质量越好。
首先,为了避免把物体抓坏,我们对每个抓握点i处,根据物体情况,设置一个最大抓握力。即最后总的力旋量的集合,为CF:
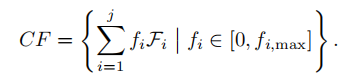
最后我们的度量Qual(F),就可以看能装到这个多面体内部的单位球的半径。

另外由于力和力矩单位不同,因此选取被抓握物体的特征长度r,通过m/r把力矩m变为力。另外由于力矩的大小和原点选择有关,可以同意选在质心处进行衡量。
为形封闭选取接触
首先根据平面或空间物体,选取4个或7个候选抓握点,确认好初值以后,再进行优化。优化的目标函数就是形封闭质量的度量。
接触力和摩擦力
这个明天再写,太晚了。待续....




![[ROC-RK3399-PC Pro] 手把手教你移植主线Buildroot(基于2023.02-rc3版本)](https://img-blog.csdnimg.cn/a4a420ba60fb4a618bb8ea1b3a9e4f53.png)