一.快速排序
1.基本介绍
快速排序(Quicksort〉是对冒泡排序的一种改进,都属于交换排序。基本思想是:通过一趟排序将要排序的数据分割成独立的两部分(每次选择中轴值),中轴值左边的元素小于中轴值,中轴值右边的元素全部大于中轴值(但不要求有序),然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列

2.基本思路
我们每次选择一个中轴值,将中轴值和最后一个元素交换位置,对left到right-1的元素进行交换,当r<=l,此时l停留到的位置和right位置上的元素(中轴值)进行交换,这个时候,l停留的位置上是中轴值,并且左边的元素比中轴值小,右边的元素比中轴值大,然后递归对左边和右边的元素进行快速排序,直到left>=right的时候停止,此时数组便是有序的了.
1.关于中轴值的选择
大部分的可能给出的是选择第一个元素作为中轴值,但是这种做法有一定的弊端,如果是数组的元素是随机排序的,是可以接受的,但是如果数组的元素是预排序或者反序的,这样所有的元素不是全被划入到中轴值左边,就是划入到中轴值右边,那么时间复杂度就会很高
一种有效的方法时是采用随机产生一个下标为[left,right]的下标,这种情况下虽然可能会产生上面描述的情况,但总的来说可能性还是很小的.
还有一种方法是:三数中值分割法,我们选取三个数,使得三个数的最大值作为中轴值进行分割,一般来说我们选取左端,中端,右端的三个元素的终止作为中轴值,这种选取的方法还是
2.小数组情形
对于很小的数组(数组元素个数小于20),快速排序不如插入排序,因为快速排序是递归的.我们通常的做法是对于小的数组采用插入排序,一种好的截止范围是n=10,同时这种做法也避免了三数中值分割法的错误情况,比如最终数组的元素只有一个元素或者两个元素,而无法三数分割
3.时间复杂度
快速排序的平均时间复杂度:O(nlogn)
最好情况:O(nlogn)
最坏情况:O()
空间复杂度:O(logn)
同时快速排序不稳定,也就说元素相同的时候,原本在前边的元素,可能会最终被排序到后边
3.代码实现
1.随机值分割
public void quickSort(int[] nums, int left, int right) {
if (left >= right)
return;
int index = (int) (left + Math.random() * (right - left + 1));
int pivot = nums[index];//随机值生成index
swap(nums, index, right);
int l = left, r = right - 1;
while (true) {
while (l < right && nums[l] < pivot) {//找到第一个比pivot大的数
l++;
}
while (r > 0 && nums[r] > pivot) {//
r--;
}
if (l < r)
swap(nums, l++, r--);
else
break;
}
swap(nums, l, right);
quickSort(nums, left, l - 1);
quickSort(nums, l + 1, right);
}
2.三数中值分割法
public static final int CUTOFF = 10;
public int median(int[] nums, int left, int right) {
int center = (left + right) / 2;
if (nums[left] > nums[center])
swap(nums, left, center);//此时center大于left
if (nums[left] > nums[right])
swap(nums, left, right);//此时left为最小
if (nums[center] > nums[right])
swap(nums, center, right);
//把center值放到right-1的位置
swap(nums, center, right - 1);
return nums[right - 1];
}
public void quickSort2(int[] nums, int left, int right) {
//cutoff为截断值
if (left + CUTOFF <= right) {
int pivot = median(nums, left, right);//随机值生成index
int l = left+1, r = right - 2;
while (true) {
while (nums[l] < pivot) {//找到第一个比pivot大的数
l++;
}
while (nums[r] > pivot) {//
r--;
}
if (l < r)
swap(nums, l++, r--);
else
break;
}
swap(nums, l, right-1);
quickSort2(nums, left, l - 1);
quickSort2(nums, l + 1, right);
} else {
insertSort(nums, left, right);
}
}
public void insertSort(int[] nums, int left, int right) {
int j;
for (int i = left; i <= right; ++i) {
int temp = nums[i];
//寻找插入的位置
for (j = i; j > left && temp < nums[j - 1]; j--) {
nums[j] = nums[j - 1];
}
nums[j] = temp;
}
}
public void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}2.快速选择
1.基本介绍
快速选择算法其实是快速排序算法的变形,主要用于解决寻找第k大元素或者第k小元素,当我们需要寻找找到(排序后)第k个元素的时候,不要求数组的所有元素必须有序,这个时候我们可以选择使用快速选择算法,因为快速选择算法的时间复杂度比直接使用快速排序的时间复杂度低
快速选择的时间复杂度:O(n)
快速排序的时间复杂度:O(nlog(n))
①中轴值最终能交换到第k个位置,说明我们找到了第k个元素
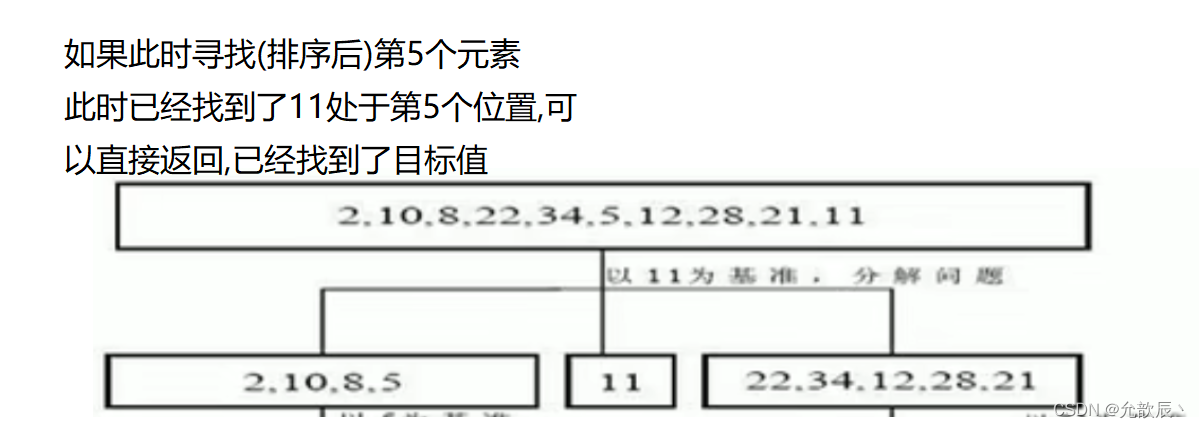
②中轴值最终的位置大于第k个位置,此时我们只需要对中轴值左边的元素进行快速排序
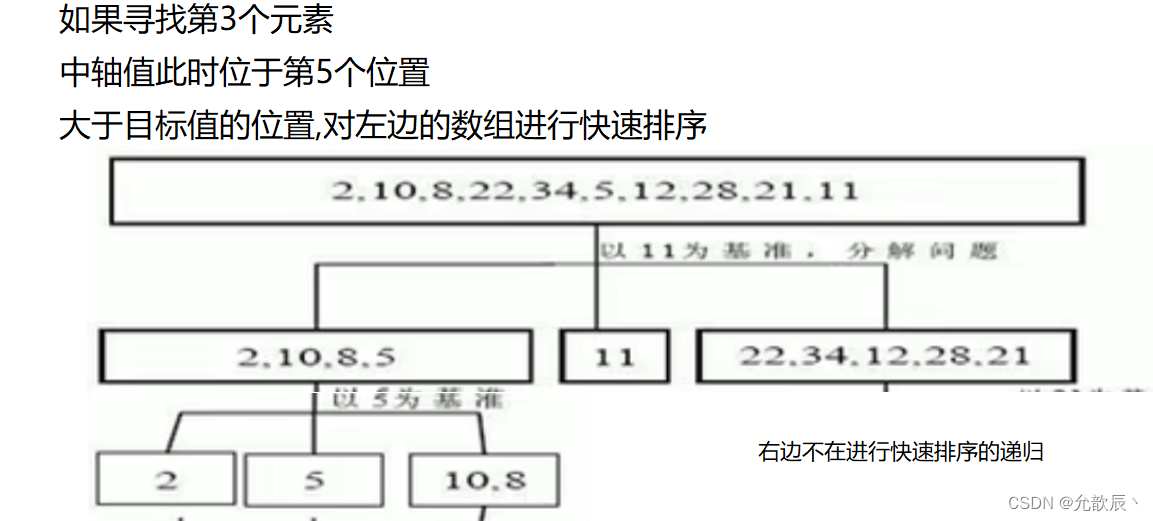
③中轴值最终的位置小于第k个位置,此时我们只需要对中轴值右边的元素进行快速排序
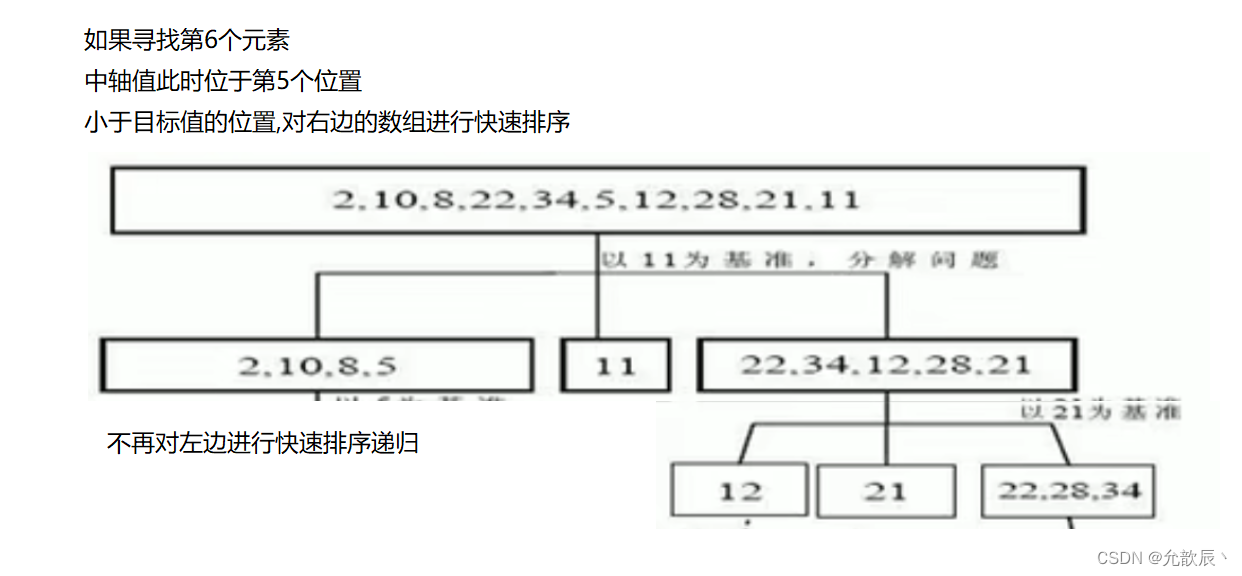
2.基本思路
快速选择的基本思路和快速排序算法还是一样的,无非就是多加了一个判断,判断是对中轴值左边进行快速排序,还是右边进行.
3.代码实现
1.随机值分割
public void quickSelect(int[] nums, int left, int right, int k) {
if (left >= right)
return;
int index = (int) (left + Math.random() * (right - left + 1));
int pivot = nums[index];//随机值生成index
swap(nums, index, right);
int l = left, r = right - 1;
while (true) {
while (l < right && nums[l] < pivot) {//找到第一个比pivot大的数
l++;
}
while (r > 0 && nums[r] > pivot) {//
r--;
}
if (l < r)
swap(nums, l++, r--);
else
break;
}
swap(nums, l, right);
if (l > k) {
quickSelect(nums, left, l - 1, k);
} else if (l < k) {
quickSelect(nums, l + 1, right, k);
}
}
2.三数中值分割法
public static final int CUTOFF = 10;
public int median(int[] nums, int left, int right) {
int center = (left + right) / 2;
if (nums[left] > nums[center])
swap(nums, left, center);//此时center大于left
if (nums[left] > nums[right])
swap(nums, left, right);//此时left为最小
if (nums[center] > nums[right])
swap(nums, center, right);
//把center值放到right-1的位置
swap(nums, center, right - 1);
return nums[right - 1];
}
public void quickSelect2(int[] nums, int left, int right, int k) {
if (left + CUTOFF <= right) {
int pivot = median(nums, left, right);
int l = left + 1, r = right - 2;
while (true) {
while (l < right && nums[l] < pivot) {//找到第一个比pivot大的数
l++;
}
while (r > 0 && nums[r] > pivot) {//
r--;
}
if (l < r)
swap(nums, l++, r--);
else
break;
}
swap(nums, l, right - 1);
if (l > k) {
quickSelect2(nums, left, l - 1, k);
} else if (l < k) {
quickSelect2(nums, l + 1, right, k);
}
} else {
insertSort(nums, left, right);
}
}
public void insertSort(int[] nums, int left, int right) {
int j;
for (int i = left; i <= right; ++i) {
int temp = nums[i];
//寻找插入的位置
for (j = i; j > left && temp < nums[j - 1]; j--) {
nums[j] = nums[j - 1];
}
nums[j] = temp;
}
}
public void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}3.数组中的第K个最大元素
1.题目描述
给定整数数组
nums和整数k,请返回数组中第k个最大的元素。请注意,你需要找的是数组排序后的第
k个最大的元素,而不是第k个不同的元素。你必须设计并实现时间复杂度为
O(n)的算法解决此问题。
力扣:力扣
2.思路分析
看到题目我们就可以想到这一题可以使用快速选择算法肯定会更加高效,寻找第k个最大的元素,也就是寻找到nums.length-k个元素是什么即可,当然我们也可以直接快速排序,直接返回nums.length-k个元素
3.代码实现
1.直接使用快速排序
public int findKthLargest(int[] nums, int k) {
quickSort(nums, 0, nums.length - 1);
return nums[nums.length - k];
}
public void quickSort(int[] nums, int left, int right) {
if (left >= right)
return;
int index = (int) (left + Math.random() * (right - left + 1));
int pivot = nums[index];//随机值生成index
swap(nums, index, right);
int l = left, r = right - 1;
while (true) {
while (l < right && nums[l] < pivot) {//找到第一个比pivot大的数
l++;
}
while (r > 0 && nums[r] > pivot) {//
r--;
}
if (l < r)
swap(nums, l++, r--);
else
break;
}
swap(nums, l, right);
quickSort(nums, left, l - 1);
quickSort(nums, l + 1, right);
}
public void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}2.快速选择
public int findKthLargest(int[] nums, int k) {
quickSelect(nums, 0, nums.length - 1,nums.length-k);
return nums[nums.length - k];
}
public void quickSelect(int[] nums, int left, int right, int k) {
if (left >= right)
return;
int index = (int) (left + Math.random() * (right - left + 1));
int pivot = nums[index];//随机值生成index
swap(nums, index, right);
int l = left, r = right - 1;
while (true) {
while (l < right && nums[l] < pivot) {//找到第一个比pivot大的数
l++;
}
while (r > 0 && nums[r] > pivot) {//
r--;
}
if (l < r)
swap(nums, l++, r--);
else
break;
}
swap(nums, l, right);
if (l > k ) {
quickSelect(nums, left, l - 1,k);
} else if (l < k ) {
quickSelect(nums, l + 1, right,k);
}
}
public void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}4.数组中的第K个最大元素
1.题目描述
给你一个二维矩阵
matrix和一个整数k,矩阵大小为m x n由非负整数组成。矩阵中坐标
(a, b)的 值 可由对所有满足0 <= i <= a < m且0 <= j <= b < n的元素matrix[i][j](下标从 0 开始计数)执行异或运算得到。请你找出
matrix的所有坐标中第k大的值(k的值从 1 开始计数)。
力扣:力扣
2.思路分析
这一题首先需要解决的就是将所有坐标的异或运算的结果表达出来,然后用一个ArrayList存起来,然后这个时候我们就可以使用快速选择求出来第k大的值了.
首先我们需要解决的就是各个位置的异或结果的值,一想到异或,并且题目中明确表达出 满足0 <= i <= a < m 且 0 <= j <= b < n 的元素 matrix[i][j],这个时候我们可以想到使用异或前缀和进行解答,我们这个时候需要找到进行递推的异或表达式
借用力扣官方题解的一幅图片,我们可以看出来异或递推公式为
prefix[i][j] = prefix[i - 1][j] ^ prefix[i][j - 1] ^ prefix[i - 1][j - 1] ^ matrix[i - 1][j - 1];
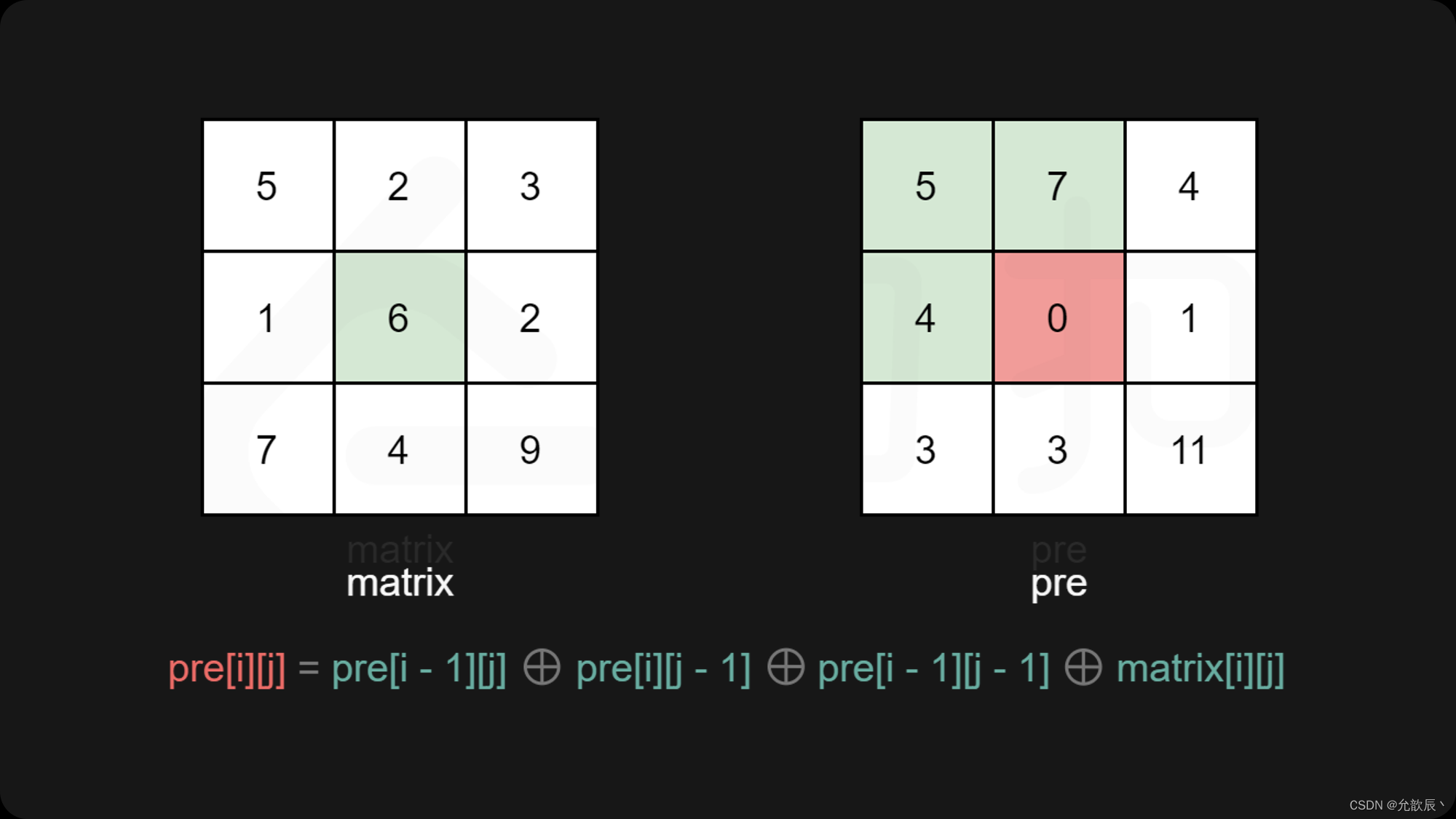
但我们我们看出(i,j)需要上一层的元素进行递推得到,如果我们定义的前缀异或的表达式长度为二维数组的大小的话,这个时候我们需要对第一行和第一列进行初始化,这个时候是很麻烦的,这个时候我们不妨定义的长度为m+1和n+1,刚开始元素的值都为1,并且一个值异或0还是本身,正好符合本题的意思
接下来进行快速选择,和上一题一样
3.代码实现
1.直接使用快速排序
public int kthLargestValue(int[][] matrix, int k) {
int m = matrix.length;
int n = matrix[0].length;
int[][] prefix = new int[m + 1][n + 1];
ArrayList<Integer> list = new ArrayList<>();
for (int i = 1; i <= m; ++i) {
for (int j = 1; j <= n; ++j) {
prefix[i][j] = prefix[i - 1][j] ^ prefix[i][j - 1] ^ prefix[i - 1][j - 1] ^ matrix[i-1][j-1];
list.add(prefix[i][j]);
}
}
quickSort(list, 0, list.size() - 1);
return list.get(list.size() - k);
}
public void quickSort(List<Integer> list, int left, int right) {
if (left >= right)
return;
int index = (int) (left + Math.random() * (right - left + 1));
int pivot = list.get(index);//随机值生成index
swap(list, index, right);
int l = left, r = right - 1;
while (true) {
while (l < right && list.get(l) < pivot) {//找到第一个比pivot大的数
l++;
}
while (r > 0 && list.get(r) > pivot) {//
r--;
}
if (l < r)
swap(list, l++, r--);
else
break;
}
swap(list, l, right);
quickSort(list, left, l - 1);
quickSort(list, l + 1, right);
}
public void swap(List<Integer> list, int i, int j) {
int temp = list.get(i);
list.set(i, list.get(j));
list.set(j, temp);
}2.快速选择
public int kthLargestValue(int[][] matrix, int k) {
int m = matrix.length;
int n = matrix[0].length;
int[][] prefix = new int[m + 1][n + 1];
ArrayList<Integer> list = new ArrayList<>();
for (int i = 1; i <= m; ++i) {
for (int j = 1; j <= n; ++j) {
prefix[i][j] = prefix[i - 1][j] ^ prefix[i][j - 1] ^ prefix[i - 1][j - 1] ^ matrix[i-1][j-1];
list.add(prefix[i][j]);
}
}
quickSelect(list, 0, list.size() - 1, list.size() - k);
return list.get(list.size() - k);
}
public void quickSelect(List<Integer> list, int left, int right, int k) {
if (left >= right)
return;
int index = (int) (left + Math.random() * (right - left + 1));
int pivot = list.get(index);//随机值生成index
swap(list, index, right);
int l = left, r = right - 1;
while (true) {
while (l < right && list.get(l) < pivot) {//找到第一个比pivot大的数
l++;
}
while (r > 0 && list.get(r) > pivot) {//
r--;
}
if (l < r)
swap(list, l++, r--);
else
break;
}
swap(list, l, right);
if (l > k) {
quickSelect(list, left, l - 1, k);
} else if (l < k) {
quickSelect(list, l + 1, right, k);
}
}
public void swap(List<Integer> list, int i, int j) {
int temp = list.get(i);
list.set(i, list.get(j));
list.set(j, temp);
}
![[ROC-RK3399-PC Pro] 手把手教你移植主线Buildroot(基于2023.02-rc3版本)](https://img-blog.csdnimg.cn/a4a420ba60fb4a618bb8ea1b3a9e4f53.png)

![[计算机组成原理(唐朔飞 第2版)]第三章 系统总线(学习复习笔记)](https://img-blog.csdnimg.cn/a79ef94d6a4c4fe984f1428eee44cb0c.png)

![[洛谷-P3698][CQOI2017]小Q的棋盘](https://img-blog.csdnimg.cn/bffd61adb75448848235fbf907371e8c.png)



