作者 | FesianXu

前言

最近基于AI的换脸应用非常的火爆，同时也引起了新一轮的网络伦理大讨论。如果光从技术的角度看，对于视频中的人体动作信息，通常可以通过泰勒展开分解成零阶运动信息与一阶运动信息，如文献[1,2]中提到的，动作的分解可以为图片动画化提供很好的光流信息，而图片动画化是提供换脸技术的一个方法。笔者在本文将会根据[1,2]文献中的内容，对其进行笔记和个人理解的探讨。 如有谬误请联系指出，转载请联系作者并注明出处，谢谢。

---

注意：本文只是基于[1,2]文献的内容阐述思路，为了行文简练，去除了某些细节，如有兴趣，请读者自行翻阅对应论文细读。

$\Delta$ 本文使用术语纪要：

<1>. 指引视频(Guided Video)，驱动视频(Driving Video)：指的是给定的用于提供动作信息的视频，该视频负责驱动，引导图片的动态信息，这两个术语在本文中将会视场合混用。

<2>. 静态图(Source Image, Source Frame)：需要被驱动的图片，其主体类别通常需要和指引视频中的类别一致，主体身份可以不同。

<3>. 泰勒展开(Taylor Expansion)：将复杂的非线性函数通过展开的方式变换成若干项的线性组合。

<4>. 变形(deformation)：指的是通过某些控制点去操控一个图片的某些部位，使得图片像素发生移动或者插值，从而形成一定程度空间上变化。

<5>. 主体（entity）：指的是图片或者视频中的活动主体，该主体不一定是人体，也可能是其他任意的物体。这里要明确的是本文提到的 主体类别（entity category） 和 主体身份（entity identity），主体身份不同于类别，比如都是人脸，一个张三的人脸，而另一个是李四的人脸。

<6>. 稀疏光流图（Sparse Optical Flow Map）：表示不同帧之间，稀疏的关键点之间的空间变化，是一个向量场。

<7>. 密集光流图（Dense Optical Flow Map）：表示不同帧之间，每个像素之间的空间变化，是一个向量场。

---

从图片动画化说起

我们知道最近的基于AI的换脸应用非常火爆，也引起了一轮轮关于AI使用的伦理大讨论，这从侧面反映了AI技术应用在我们日常生活的渗透。如Fig 1.1所示，给定一个指引视频，让一张静态图片跟随着该视频表演其中的表情（或者动作），这种技术的主要框架在于需要分离指引视频中的动作信息（motion）和外观信息（appearance），将提取出的动作信息以某种形式添加到静态图上，让静态图达到一定程度的变形（deformation），以达到图片动态化表演特定动作的目的。

这类型的工作可以称之为图片动画化 （image animation），指的是给定一张具有某个主体的静态图（Source Image）（主体不一定是人体，如Fig 1.2所示，不过我们这里主要以人体做例子），再给定一个由该主体表演某个动作的视频，一般称之为驱动视频（Driving Video），让静态图跟随着驱动视频的动作“活动”起来。注意到静态图和驱动视频中的主体是同一类型的主体，但是身份可能是不同的，比如都是人脸，但是不是同一个人的人脸。如Fig 1.3所示，给定了一个驱动视频，其主体是一个人脸的表情序列，给定了一个静态图，主体是一个不同身份的人，然后任务期望提取出序列中的动作信息，期望以某种方法添加到静态图上，使得静态图可以通过像素变形的方式，形成具有指定动作，但是主体身份和静态图一致的新的动作序列。

当然，该任务不一定被局限在人脸上，如Fig 1.2所示，事实上，只要输入驱动视频和静态图的主体类别一致，就可以通过某些自监督的方法进行动作信息提取，并且接下来进行动作信息迁移到目标静态图上的操作。

我们现在已经对图片动画化有了基本的认识，那么从技术上看，这整个任务的难点在于哪儿呢？主要在于以下几点：

1. 如何表征运动信息？
2. 如何提取驱动视频中的运动信息？
3. 如何将提取到的动作信息添加到静态图中，让静态图变形？

通常来说，表征一个主体的运动信息可以通过密集光流图的方式表达，光流（optical flow）[5] 表示的是某个局部运动的速度和方向，简单地可以理解为在时间很短的两个连续帧的某个局部，相对应像素的变化情况。如Fig 1.4所示，如果计算(a)(b)两帧关于蓝色框内的光流，我们可以得到如同（c）所示的光流图，表征了这个“拔箭”动作的局部运动速度和方向，因此是一个向量场，我们通常可以用$\mathcal{F}\in {\mathbb{R}}^{H\times W\times 2}$表示，其中的$H\times W$表示的是局部区域的空间尺寸，维度2表示的是二维空间$(\Delta x,\Delta y)$偏移。如果该局部区域的每一个像素都计算光流图，那么得到的光流图就称之为 密集光流图（Dense Optical Flow Map），如Fig 1.4 （c）所示。密集光流图中的每一个像素对应的向量方向，提供了从一个动作转移到下一个动作所必要的信息，是图片动画化过程中的必需信息。

如果能够给出某个运动的密集光流图，那么就可以根据每个像素对应在光流图中的向量方向与大小对像素进行位移插值后，实现图像的变形的过程。然而，在图片动画化过程中，我们的输入通常如Fig 1.5所示，其静态图和驱动视频中的某一帧（称之为驱动帧）之间的动作差别很大，而且主体的身份还不一定一致，能确定的只有 一点，就是： 稀疏的关键点可以视为是一一配对的。 如Fig 1.3所示，蓝色点是人体的稀疏关键点，通常存在一对一的配对映射（暂时不考虑遮挡），如黄色虚线所示，这种稀疏关键点的映射图，我们称之为 稀疏光流图 （Sparse Optical Flow Map）。我们接下来介绍的文章，都是 **从不同方面考虑从稀疏光流图推理出密集光流图，从而指引图片变形的。 **

到此为止，我们之前讨论了如何定义一个动作的运动信息，也就是用密集光流图表示。同时，我们也分析了一种情况，在实际任务中，很难直接得到密集光流图，因此需要从一对一配对的稀疏光流图中加入各种先验知识，推理得到密集光流图。我们接下来的章节讨论如何添加这个先验知识。

为了以后章节的讨论方便，我们给出图片动画化模型的基本结构，如Fig 1.6所示，需要输入的是驱动视频和静态图，静态图具有和驱动视频相同的主体类别（比如都是人）但是身份可以不同（比如是不同的人），期望生成具有和静态图相同身份和主体，动作和驱动视频一致的视频，通常是提取驱动视频中每帧的动作信息，结合静态图生成期望的视频帧，在拼接成最终的视频输出。

无监督关键点提取

在继续讨论密集光流图提取之前，我们首先描述下如何提取稀疏光流信息，也即是稀疏的关键点信息，如Fig 1.5所示。当然，对于人体而言，目前已经有很多研究可以进行人体姿态估计，比如OpenPose [6]，AlphaPose [7]等，这些研究可以提取出相对不错的人体关键点。就人脸这块的关键点提取而言，也有很多不错的研究[8]，可以提取出相对不错的人脸稀疏或者密集关键点，如Fig 2.1所示。

但是，我们注意到，为了提取人体或者人脸的关键点，目前的大多数方法都需要依赖于大规模的人体/人脸标注数据集，这个工作量非常大，因此，假如我们需要对某些非人脸/人体的图片进行图片动画化，比如Fig 2.2所示的动画风格的马，我们将无法通过监督学习的方式提取出关键点，因为没有现存的关于这类型数据的数据集。为了让图片动画化可以泛化到人体/人脸之外更广阔的应用上，需要提出一种无监督提取特定主体物体关键点的方法。

文献[1,2,11]利用了一种无监督的关键点提取方法，这里简单介绍一下，为之后的章节提供铺垫。如Fig 2.3所示，对于输入的单帧RGB图片$\mathbf{I}\in {\mathbb{R}}^{H\times W\times 3}$来说，利用U-net [12]提取出$K$个热值图$H_k\in [0,1{]}^{H\times W},k\in [1,\cdots ,K]$，每$k$个热值图表示了第$k$个关节点的分布情况。当然，U-net的最后一层需要用softmax层作为激活层，这样解码器的输出才能解释为每个关键点的置信图(confidence map)。

然而，我们还需要从置信图中计算得到关键点的中心位置和关节点的方差¹（方差以超像素的角度，表示了对关键点预测的可靠性），因此用高斯分布去对置信图进行拟合，得到均值和方差。对于每个关键点的置信图$H_k\in [0,1{]}^{H\times W}$，我们有：
$$\begin{array}{rl}{\mathbf{h}}_k& =\sum _{p\in \mathcal{U}}{H}_k[p]p\\ {\Sigma }_k& =\sum _{p\in \mathcal{U}}{H}_k[p](p-{\mathbf{h}}_k)(p-{\mathbf{h}}_k{)}^{\mathrm{T}}\end{array}\text{\hspace{1em}(2.1)}$$
其中${\mathbf{h}}_k\in {\mathbb{R}}^2$表示了第$k$个关键点的置信图的中心坐标，而${\Sigma }_k\in \mathbb{R}$则是其方差。$\mathcal{U}$表示了图片坐标的集合，而$p\in \mathcal{U}$则是遍历了整个置信图。整个过程如Fig 2.4所示，通过式子(2.1)，最终需要将置信图更新为以高斯分布表示的形式，如(2.2)所示。
$$\begin{gathered} H_k(\mathbf{p})=\frac{1}{\alpha }\exp (-(\mathbf{p}-{\mathbf{h}}_k){\Sigma }_k^{-1}(\mathbf{p}-{\mathbf{h}}_k)) \\ \forall p\in \mathcal{U}\text{\hspace{1em}(2.2)} \end{gathered}$$
其中的$\alpha$为标准化系数。最终得到的置信图如Fig 2.4的右下图所示。

至今，我们描述了如何提取关键点，但是这个关键点还没有经过训练，因此其输出还是随机的，不要担心，我们后续会一步步介绍如何进行无监督训练。不过这一章节就此为止吧，为了后续章节的方便，我们先假设我们的 关键点提取是经过训练的，可以提取出较为完美的关键点 。

稀疏光流图

在引入动作分解的概念之前，我们先花时间去讨论下稀疏光流图。如Fig 3.1所示，假设我们有训练好的关键点检测器，表示为$\Delta$，那么输入同一个视频中的不同两帧（我们在后面会解释为什么在训练时候是输入同一个视频的不同两帧），其中用$\mathbf{x}$表示静态图，用${\mathbf{x}}^{\prime }$表示驱动视频（训练时候是和静态图一样，出自同一个视频）中的其中一帧，那么，检测出的关键点可以表示为:
$$\begin{array}{rl}H& =\Delta (\mathbf{x})\\ H^{\prime }& =\Delta ({\mathbf{x}}^{\prime })\end{array}\text{\hspace{1em}(3.1)}$$
那么，自然地，这两帧之间的对应关键点的相对变化可以简单地用“代数求差”表示，为：
$$\dot{H}=H^{\prime }-H\text{\hspace{1em}(3.2)}$$
这里的$\dot{H}$称之为稀疏光流图，其表示了稀疏关键点在不同帧之间的空间变化，其中每一个关键点的光流表示为$h_k=[\Delta x,\Delta y]$。可知$\dot{H}\in {\mathbb{R}}^{K\times 2}$，其中$K$是关键点的数量。

但是得到稀疏光流图只能知道关键点是怎么位移形变的，我们该怎么求出关键点周围的像素的位移变化数据呢？

动作分解与泰勒展开

知道了稀疏光流图，我们只知道关键点是怎么变化的，但是对关键点周围的像素的变化却一无所知，我们最终期望的是通过稀疏光流图去推理出密集光流图，如Fig 4.1所示。

为了实现这个过程，我们需要引入先验假设，而最为直接的先验假设就是动作分解。

零阶动作分解

一种最简单的动作分解假设就是：

每个关键点周围的主体部件是局部刚性的，因此其位移方向和大小与关键点的相同，我们称之为动作零阶分解。

这个假设通过Fig 4.2可以得到很好地描述，我们通过关键点检测模型可以检测出对应的关键点位移，根据假设，那么周围的身体部分，如橘色点虚线框所示，是呈现刚体变换的，也就是说该区域内的所有和主体有关的部分的像素的位移向量，都和该关键点相同。

那么现在问题就在于，这里谈到的每个关键点的“周围区域”到底有多大，才会使得刚体性质的假设成立。于是问题变成去预测对于每个关节点来说，能使得刚体性质成立的区域了。对于每个关键点，我们通过神经网络预测出一个掩膜$M_k\in {\mathbb{R}}^{H\times W}$，那么我们有：
$${\mathcal{F}}_{\mathrm{coarse}}=\sum _{k=1}^{K+1}{M}_k\otimes \rho (h_k)\text{\hspace{1em}(4.1)}$$
其中的$\rho (\cdot )$表示对每个关键点的光流重复$H\times W$次，得到$\rho (\cdot )\in {\mathbb{R}}^{H\times W\times 2}$的张量，该过程如Fig 4.3所示，当然这里用箭头的形式表示了光流向量，其实本质上是一个${\mathbb{R}}^2$的向量；而$\otimes$表示逐个元素的相乘。

通常这个掩膜$M_k$通过U-net去进行学习得到，这里的U-net也即是Fig 4.1中的Dense Motion Network，用符号$M$表示，其设计的初衷是可以对某个关键点$k$呈现刚体区域进行显著性高亮，如Fig 4.4所示，并且为了考虑相对不变的背景，实际上需要学习出$K+1$个掩膜，其中一个掩膜用于标识背景，同时也需要$\rho ([0,0])$用于表示背景区域不曾出现位移。

除了掩膜之外，模块$M$同样需要预测${\mathcal{F}}_{\mathrm{residual}}$，作为${\mathcal{F}}_{\mathrm{coarse}}$的补充，其设计的初衷是预测某些非刚体性质的变换，非刚体性质的变换不能通过之前提到的分割主体部分然后进行掩膜的方法得到，因此需要独立出来，通过网络进行预测。于是我们有：
$$\mathcal{F}={\mathcal{F}}_{\mathrm{coarse}}+{\mathcal{F}}_{\mathrm{residual}}\text{\hspace{1em}(4.2)}$$
现在Dense Motion Network的框图如Fig 4.5所示，我们以上阐述了该模块的输出，现在考虑这个模块的输入。输入主要有稀疏光流图$\dot{H}$和静态图$\mathbf{x}$，然而在整个优化过程中，由于$\mathcal{F}$其实是和${\mathbf{x}}^{\prime }$对齐的，而输入如果只是$\mathbf{x}$的信息，那么就可能存在优化过程中的困难，因为毕竟存在较大的差别，因此需要显式地先对输入静态图进行一定的变形，可以用双线性采样（Bilinear Sample）[17] 进行，记$f_w(\cdot )$为双线性采样算符，我们有：
$${\mathbf{x}}_k=f_w(\mathbf{x},\rho (h_k))\text{\hspace{1em}(4.3)}$$
关于双线性采样的具体细节可见[17]，双线性采样可显式地实现图片变形，并且是可微分的，式子(4.3)中的$\mathbf{x}$就是采样输入input，而$\rho (h_k)$就是采样网格grid。其中的${\mathbf{x}}_k$是根据$\rho (h_k)$只对每个关键点光流进行变形形成的，将$\dot{H}$和 { x k } k = 1 , ⋯   , K \{\mathbf{x}_k\}_{k=1,\cdots,K} {xk​}k=1,⋯,K​以及$\mathbf{x}$在通道轴进行拼接，然后作为U-net的输入。

一阶动作分解

零阶动作分解的假设还是过于简单了，即便是关键点局部区域也不一定呈现出良好的刚体性质，在存在柔性衣物的影响下更是如此，因此引入了一阶动作分解的假设，除了引入的基本假设不同之外，模型其他大部分和零阶动作分解类似。在一阶动作分解下，基本假设变成了

每个关键点周围的主体部件是局部仿射变换[13]的，我们称之为一阶动作分解。

我们接下来会更加形象地用图示解释这个假设，在此之前为了和论文[2]保持一致，先定义一些符号。

我们称静态图为$\mathbf{S}\in {\mathbb{R}}^{3\times H\times W}$，相当于之前谈到的$\mathbf{x}$；称驱动视频中的某一个驱动帧为$\mathbf{D}\in {\mathbb{R}}^{3\times H\times W}$，相当于之前谈到的${\mathbf{x}}^{\prime }$。其中密集光流图$\mathcal{F}\in {\mathbb{R}}^{H\times W\times 2}$用一个变换表示，有${\mathcal{T}}_{\mathbf{S}\leftarrow \mathbf{D}}:{\mathbb{R}}^2\to {\mathbb{R}}^2$，表示从驱动帧到静态图的密集像素位置映射，我们称之为 密集光流映射。和在零阶动作分解章节不同的是，因为驱动帧的主体和静态图的主体可能差别较大（比如人体的衣着方式等），因而导致的不对齐性会影响效果，因此假设存在着一个中间态的抽象参考帧$\mathbf{R}$作为过渡，如Fig 4.6所示，其中我们称在驱动帧里面的点为$z_k\in {\mathbb{R}}^2$，在参考帧的点为$p_k\in {\mathbb{R}}^2$，在静态图的点为$w_k\in {\mathbb{R}}^2$， 不难知道有$p_k={\mathcal{T}}_{\mathbf{R}\leftarrow \mathbf{D}}(z_k)$。那么此时，我们知道密集光流映射可以分解为：
$${\mathcal{T}}_{\mathbf{S}\leftarrow \mathbf{D}}={\mathcal{T}}_{\mathbf{S}\leftarrow \mathbf{R}}\circ {\mathcal{T}}_{\mathbf{R}\leftarrow \mathbf{D}}\text{\hspace{1em}(4.4)}$$
如果假设${\mathcal{T}}_{\mathbf{R}\leftarrow \mathbf{D}}$在每个关键点局部是双射的，也即是有${\mathcal{T}}_{\mathbf{R}\leftarrow \mathbf{D}}={\mathcal{T}}_{\mathbf{D}\leftarrow \mathbf{R}}^{-1}$，那么此时式子(4.4)变为：
$${\mathcal{T}}_{\mathbf{S}\leftarrow \mathbf{D}}={\mathcal{T}}_{\mathbf{S}\leftarrow \mathbf{R}}\circ {\mathcal{T}}_{\mathbf{R}\leftarrow \mathbf{D}}={\mathcal{T}}_{\mathbf{S}\leftarrow \mathbf{R}}\circ {\mathcal{T}}_{\mathbf{D}\leftarrow \mathbf{R}}^{-1}\text{\hspace{1em}(4.5)}$$
我们发现${\mathcal{T}}_{\mathbf{S}\leftarrow \mathbf{R}},{\mathcal{T}}_{\mathbf{D}\leftarrow \mathbf{R}}$都存在一个模式，那就是都是从$\mathbf{X}\leftarrow \mathbf{R}$，因此不妨假设有一个映射${\mathcal{T}}_{\mathbf{X}\leftarrow \mathbf{R}}$，其中$\mathbf{X}$为任意帧。

精彩的地方来了！因为该映射是一个函数，因此可以通过泰勒函数展开，对于关键点$p_k$周围领域$p$进行泰勒展开，有：
$${\mathcal{T}}_{\mathbf{X}\leftarrow \mathbf{R}}(p)={\mathcal{T}}_{\mathbf{X}\leftarrow \mathbf{R}}(p_k)+(\frac{\mathrm{d}}{\mathrm{d}p}{\mathcal{T}}_{\mathbf{X}\leftarrow \mathbf{R}}(p){|}_{p=p_k})(p-p_k)+o(||p-p_k||)\text{\hspace{1em}(4.6)}$$
其中$o(||p-p_k||)$为高阶无穷小项，可以忽略，而$(\frac{\mathrm{d}}{\mathrm{d}p}{\mathcal{T}}_{\mathbf{X}\leftarrow \mathbf{R}}(p){|}_{p=p_k})(p-p_k)$就是一阶近似项，我们通过这个一阶近似项去估计关键点周围领域的变换。从式子(4.6)中我们可以发现，映射${\mathcal{T}}_{\mathbf{X}\leftarrow \mathbf{R}}(p)$取决于每个关键点以及其对应的Jacobians矩阵[14] ²，有：
$$\begin{gathered} {\mathcal{T}}_{\mathbf{X}\leftarrow \mathbf{R}}(p)\simeq \left\{\right\{{\mathcal{T}}_{\mathbf{X}\leftarrow \mathbf{R}}(p_1),\frac{\mathrm{d}}{\mathrm{d}p}{\mathcal{T}}_{\mathbf{X}\leftarrow \mathbf{R}}(p){|}_{p=p_1}\},\cdots , \\ \{{\mathcal{T}}_{\mathbf{X}\leftarrow \mathbf{R}}(p_k),\frac{\mathrm{d}}{\mathrm{d}p}{\mathcal{T}}_{\mathbf{X}\leftarrow \mathbf{R}}(p){|}_{p=p_k}\left\}\right\}\text{\hspace{1em}(4.7)} \end{gathered}$$
类似地，对式子(4.5)进行泰勒展开（具体推导见[2]的Sup. Mat.），有：
$${\mathcal{T}}_{\mathbf{S}\leftarrow \mathbf{D}}(z)\approx {\mathcal{T}}_{\mathbf{S}\leftarrow \mathbf{R}}(p_k)+J_k(z-{\mathcal{T}}_{\mathbf{D}\leftarrow \mathbf{R}}(p_k))\text{\hspace{1em}(4.8)}$$
其中：
$$J_k=(\frac{\mathrm{d}}{\mathrm{d}p}{\mathcal{T}}_{\mathbf{S}\leftarrow \mathbf{R}}(p){|}_{p=p_k})(\frac{\mathrm{d}}{\mathrm{d}p}{\mathcal{T}}_{\mathbf{D}\leftarrow \mathbf{R}}(p){|}_{p=p_k}{)}^{-1}\text{\hspace{1em}(4.9)}$$
而式子(4.8)中的${\mathcal{T}}_{\mathbf{S}\leftarrow \mathbf{R}}(p_k),{\mathcal{T}}_{\mathbf{D}\leftarrow \mathbf{R}}(p_k)$实际上关键点的稀疏光流映射，可以用之前在零阶动作分解一章中谈到的无监督关键点提取的方式获得，唯一不同的是，无论是对$\mathbf{S}$还是$\mathbf{D}$的每个关键点 $k$ 预测都要附带输出四个通道，这些输出是作为对式子(4.9)中的$\frac{\mathrm{d}}{\mathrm{d}p}{\mathcal{T}}_{\mathbf{S}\leftarrow \mathbf{R}}(p){|}_{p=p_k}$和$\frac{\mathrm{d}}{\mathrm{d}p}{\mathcal{T}}_{\mathbf{D}\leftarrow \mathbf{R}}(p){|}_{p=p_k}$系数的估计（具体细节还请移步论文[2]）。

这个时候的$J_k\in {\mathbb{R}}^{2\times 2}$是该映射的Jacobians矩阵，当$J_k=\mathbb{I}$（其中$\mathbb{I}$为单位矩阵）时，此时退化为零阶动作分解。因为此时显然有:
$$\begin{array}{rl}{\mathcal{T}}_{\mathbf{S}\leftarrow \mathbf{D}}(z)& \approx {\mathcal{T}}_{\mathbf{S}\leftarrow \mathbf{R}}(p_k)+z-{\mathcal{T}}_{\mathbf{D}\leftarrow \mathbf{R}}(p_k)\\ & =z-({\mathcal{T}}_{\mathbf{D}\leftarrow \mathbf{R}}(p_k)-{\mathcal{T}}_{\mathbf{S}\leftarrow \mathbf{R}}(p_k))\\ & =z-(H^{\prime }-H)\\ & =z-\dot{H}\end{array}\text{\hspace{1em}(4.10)}$$
其中的$\dot{H}$就是式子(3.2)中提到的稀疏光流图，因此零阶动作分解的实质就是局部刚性变换。

由此，我们可以从几何变换上解释动作的一阶分解，因为$z^{\prime }\in {\mathbb{R}}^{2\times 1}=z-{\mathcal{T}}_{\mathbf{D}\leftarrow \mathbf{R}}(p_k)$可以视为是关键点$p_k$周围领域与关键点之间的位移，这个位移乘上Jacobians矩阵$J_k\in {\mathbb{R}}^{2\times 2}$就是一阶近似项。不妨假设：
$$\begin{array}{rl}{J}_k& =\left[\begin{array}{cc}{J}_{11}& J_{12}\\ J_{21}& J_{22}\end{array}\right]\\ z^{\prime }& =[z_1,z_2{]}^{\mathrm{T}}\end{array}\text{\hspace{1em}(4.11)}$$
因此考虑到式子(4.8)，有：
$$\begin{array}{rl}{z}_1^{\prime }& =J_{11}{z}_1+J_{12}{z}_2\\ z_2^{\prime }& =J_{21}{z}_1+J_{22}{z}_2\end{array}\text{\hspace{1em}(4.12)}$$
可以视为是对$z^{\prime }$的旋转，尺度放缩和切变（不包括平移，因为没有偏移项，具体可见仿射变换具体定义[15]），因此称之为是 （关键点）局部的仿射变换先验假设就是一阶动作分解的本质。

那么整理起来，我们的整个框图如Fig 4.7所示，和零阶动作分解框图Fig 4.1不同的是，其预测并且添加了Jacobians矩阵项。

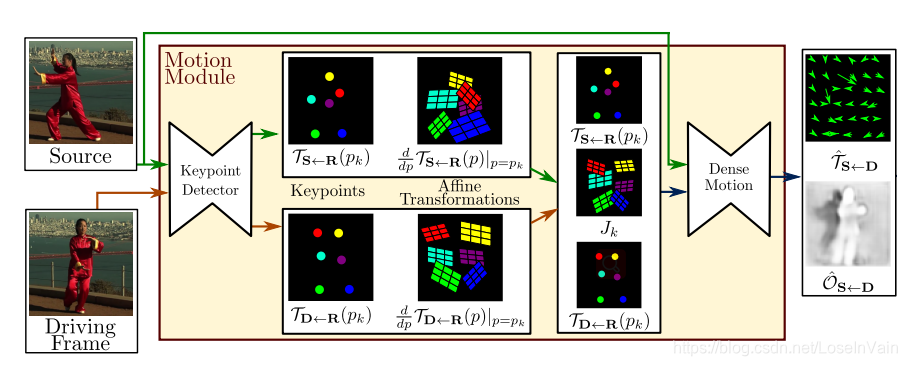
当然，同样我们需要通过稀疏光流映射去估计密集光流映射，因此同样会有Dense Motion网络，这个网络和Fig 4.5类似，会去预测出掩膜$M_k$，该掩膜的作用和零阶动作分解的作用一致，如Fig 4.4所示。那么有密集光流映射估计${\hat{\mathcal{T}}}_{\mathbf{S}\leftarrow \mathbf{D}}(z)$：
$${\hat{\mathcal{T}}}_{\mathbf{S}\leftarrow \mathbf{D}}(z)=M_{0}z+\sum _{k=1}^K{M}_k({\mathcal{T}}_{\mathbf{S}\leftarrow \mathbf{R}}(p_k)+J_k(z-{\mathcal{T}}_{\mathbf{D}\leftarrow \mathbf{R}}(p_k)))\text{\hspace{1em}(4.13)}$$
类似地，其中$M_0$是对背景的掩膜。具体该网络的输入就不再赘述了，具体见论文[2]。

需要注意的是，在文章[2]中，作者还用Dense Motion网络学习了一个掩膜${\hat{\mathcal{O}}}_{\mathbf{S}\leftarrow \mathbf{D}}$ ，该掩膜的作用是去预测被遮挡的部分，该部分不能通过密集光流进行变形得到，需要进行inpainting [16]填充，具体细节不赘述。

---

总结

在本文，我们通过引入先验，对动作进行分解，可以从稀疏光流图估计出密集光流图，通过将密集光流图输入到变形模型中，可以实现从驱动帧到静态图的转换，这个转换是实现图片动画化的一个重要技术。当然，限于篇幅，还有很多技术点没有谈到，在下个博文，我们将会介绍对应的变形模型，端到端无监督训练模式和该系列模型的缺陷等。一路不易，敬请期待，谢谢支持。

---

Reference

[1]. Siarohin, A., Lathuilière, S., Tulyakov, S., Ricci, E., & Sebe, N. (2019). Animating arbitrary objects via deep motion transfer. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (pp. 2377-2386).

[2]. Siarohin, A., Lathuilière, S., Tulyakov, S., Ricci, E., & Sebe, N. (2019). First order motion model for image animation. In Advances in Neural Information Processing Systems (pp. 7137-7147).

[3]. https://blog.csdn.net/LoseInVain/article/details/108483736

[4]. Simonyan, K., & Zisserman, A. (2014). Two-stream convolutional networks for action recognition in videos. In Advances in neural information processing systems (pp. 568-576).

[5]. https://en.wikipedia.org/wiki/Optical_flow

[6]. Cao Z , Hidalgo G , Simon T , et al. OpenPose: Realtime Multi-Person 2D Pose Estimation using Part Affinity Fields[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, PP(99):1-1.

[7]. https://github.com/MVIG-SJTU/AlphaPose

[8]. Bulat, Adrian , and G. Tzimiropoulos . “How Far are We from Solving the 2D & 3D Face Alignment Problem? (and a Dataset of 230,000 3D Facial Landmarks).” IEEE International Conference on Computer Vision IEEE Computer Society, 2017.

[9]. https://github.com/1adrianb/face-alignment

[10]. https://github.com/AliaksandrSiarohin/first-order-model

[11]. Jakab, T., Gupta, A., Bilen, H., & Vedaldi, A. (2018). Unsupervised learning of object landmarks through conditional image generation. In Advances in neural information processing systems (pp. 4016-4027).

[12]. Ronneberger, O., Fischer, P., & Brox, T. (2015, October). U-net: Convolutional networks for biomedical image segmentation. In International Conference on Medical image computing and computer-assisted intervention (pp. 234-241). Springer, Cham.

[13]. https://blog.csdn.net/LoseInVain/article/details/108454304

[14]. https://en.wikipedia.org/wiki/Jacobian_matrix_and_determinant

[15]. https://blog.csdn.net/LoseInVain/article/details/102756630

[16]. https://www.wandb.com/articles/introduction-to-image-inpainting-with-deep-learning

[17]. https://blog.csdn.net/LoseInVain/article/details/108732249

---

1. 这里采用高斯分布拟合的目的还有一个就是，在无监督训练开始时，其预测结果是随机的，将其用高斯分布去拟合，才能给后续的优化提供方便。 ↩︎

2. Jacobians矩阵[14]可以视为是多元函数的导数，在对多元函数进行泰勒展开时候常见。 ↩︎