💯💯💯💯

Ⅰ.研究链表带环问题

链表带环是什么意思呢？
就是一个链表有一个结点指向了前面结点导致又链接回来的问题
如果进行遍历就会变成死循环

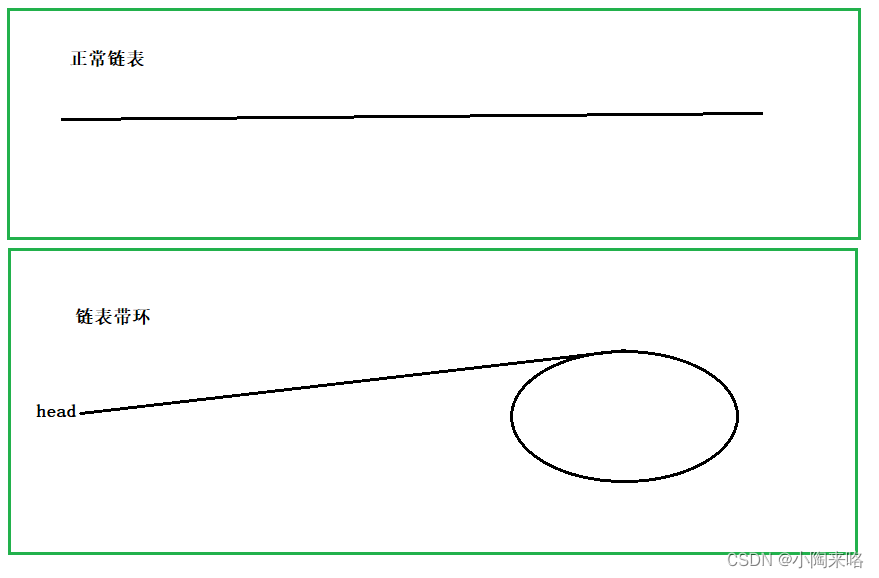
那么如何判断一个链表是否带环呢？
链表带环问题Ⅰ

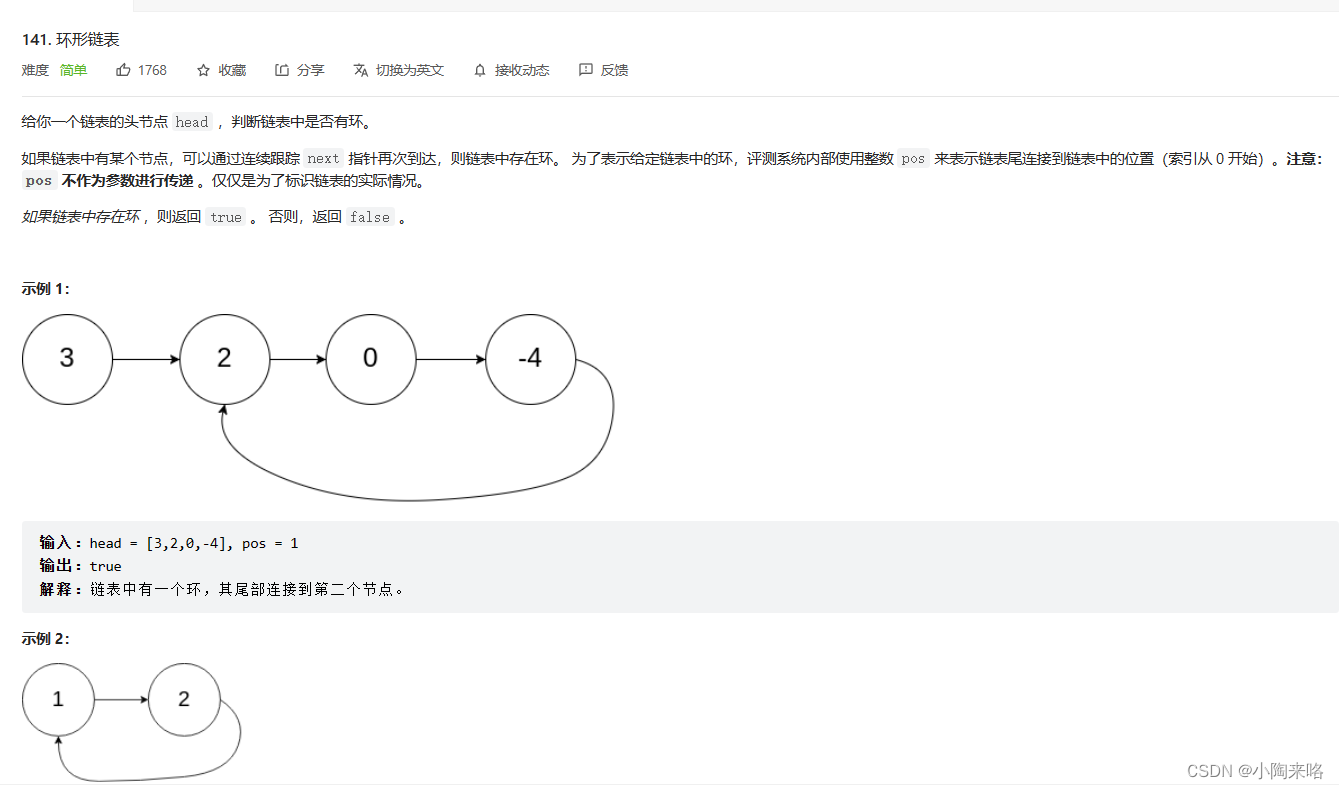
思路：
我们可以利用快慢指针，慢指针走一步，快指针走两步，当快指针进入环中时，慢指针肯定还在外面，当慢指针进环时，快指针可能已经走了好几圈，但一旦两个指针进环后，肯定会相遇，我们可以将带环问题，转换为相遇问题，也就是小学经常看到的，小明先跑50，速度为5m/s，小亮后跑速度为10m/s,问何时相遇。

我们只要判断它们是否相遇了，就能确定是否带环，因为如果没有带环的话，那就不可能相遇，快指针肯定先走出去。

快慢指针，即慢指针一次走一步，快指针一次走两步，两个指针从链表其实位置开始运行，
如果链表带环则一定会在环中相遇，否则快指针率先走到链表的末尾。

bool hasCycle(struct ListNode *head)
 {
    struct ListNode*fast,*slow;
    fast=slow=head;//快慢指针都从开头开始走
    while(fast&&fast->next)
    {
        slow=slow->next;
        fast=fast->next->next;
        if(fast==slow)//如果慢指针等于快指针则一定在环里
        return true;
    }
    return false;//否则就不在环里
}

Ⅱ.扩展带环问题

1.为什么慢指针和快指针一定会相遇？

假设链表带环，快慢指针同时走，快指针先入环，慢指针后入环，当慢指针刚入环时，有可能与快指针相遇，也有可能与快指针相差很远，但这不是问题，关键的关键是它们两都在环里，并且快指针每次走两步，慢指针每次走1步，而它们每次走一步时，它们之间的距离就减少1，每走一步，快指针就追上一步，所以它们之间的距离在不断的缩小，最后肯定能追上。

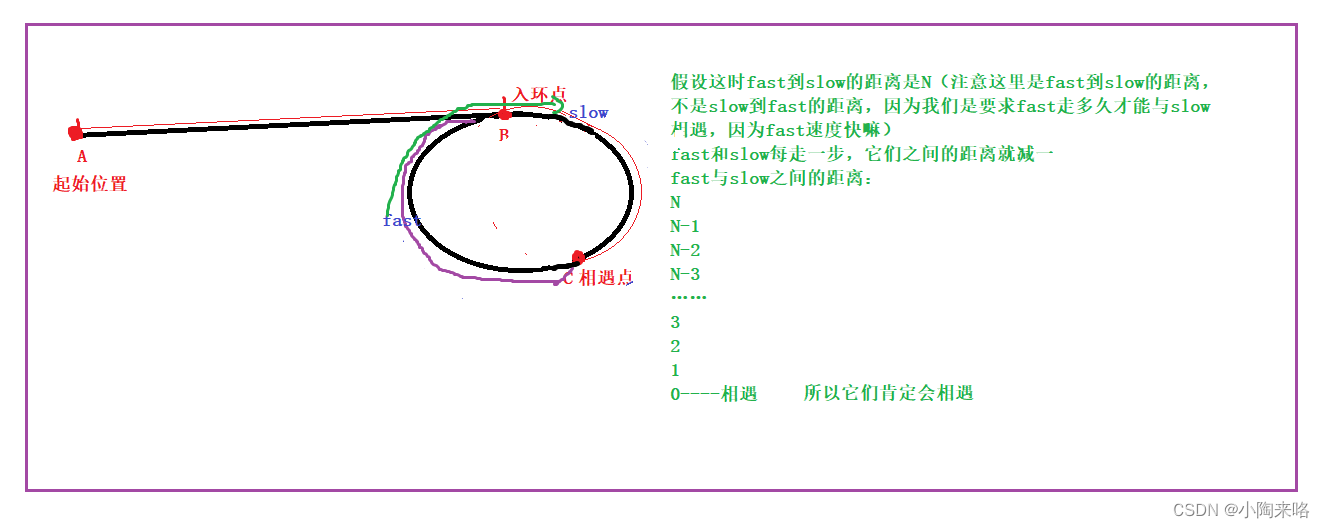
并且不会出现套圈的现象，因为两个结点之间最小的距离也就是1了，每次缩小1，最后要么重合，要么还是重合，不可能从头上跳过去的。

还有慢指针在慢指针走到一圈之前，快指针肯定是可以追得上慢指针的，即相遇
慢指针刚入环时，与快指针最远距离可能为一个环距离吧，但想一想，当慢指针走了一环距离时，快指针走了多少？快指针走的是慢指针的2倍呀，那肯定是2圈了都，慢指针走1圈，快指针都要走两圈了，这里面肯定追上慢指针了。

2.快指针一次走3步，4步…n步可以吗？

其实这种本质上看的是相对位移量，只要我们算出相对位移量就可以判断了。上面快指针每次走2步慢指针每次走1步，它们每次走一步都会缩小1距离，而因为1就是最小距离单位，所以最后肯定会相遇。
但如果一次走三步，就不一定了
假设快慢指针都入环后，它们之间的距离为N
快指针每次走3步，慢指针每次走1步，那它们每次走，快指针都会缩小2个距离，那它们之间的距离就变成了N-2，再走就变成N-4，N-6……，这里就涉及N是奇数还是偶数了，当N是偶数时，那么最后它们是可以相遇的，如果是奇数，那这圈是不会相遇的，不过最后走完快慢指针之间的距离就变成-1了，也就是这个环的周长减1距离，这又要取决于环的周长是偶数还是奇数了……。

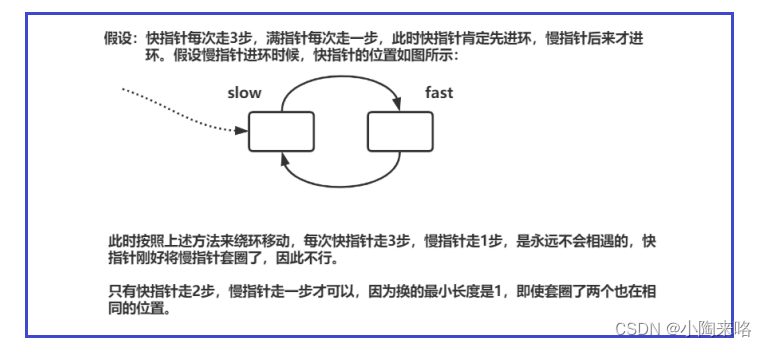
如果快指针每次走4步，道理也是一样的，在快慢指针都入环后，假设它们的距离为N
则每次距离都会缩小3，则最好是否相遇取决于N是否是3的倍数了。

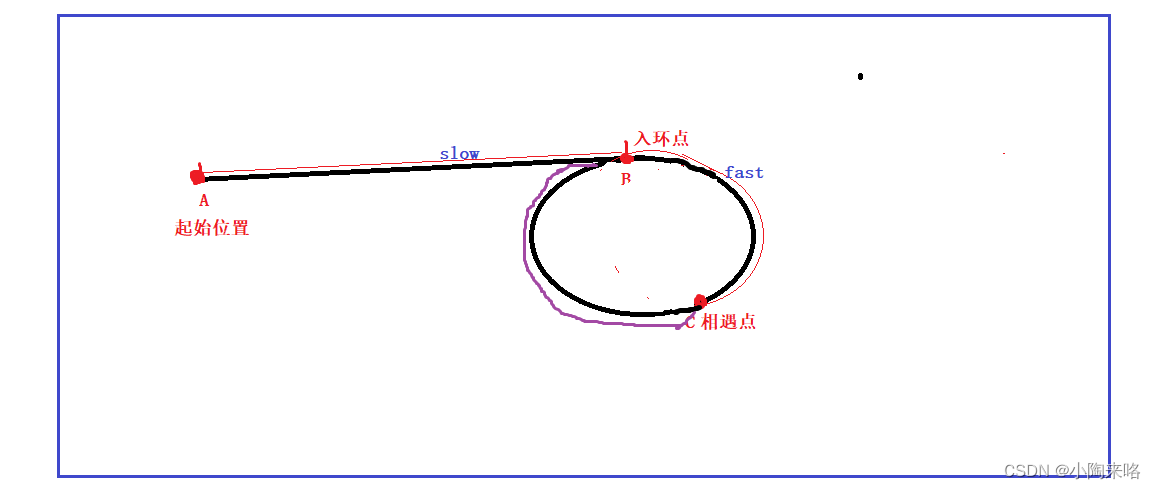
3.慢指针走的距离和快指针走的距离？

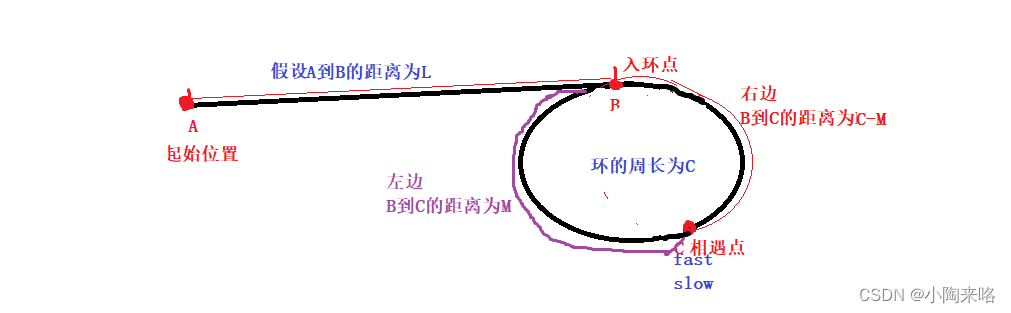
你想一想快指针和慢指针在相遇前总共走了多远距离呢？
快慢指针是同时从开始位置走的，快指针走的快，先入环，慢指针走的慢，后入环。
前面我们知道fast在slow走满一圈之前追上，所以slow不可能走过一圈的，所以慢指针走的总距离为L+M

而快指针就不一定了，快指针走的快，先入环，谁知道它在环里走了多少圈了都，而且走的圈数越多说明这个环越小

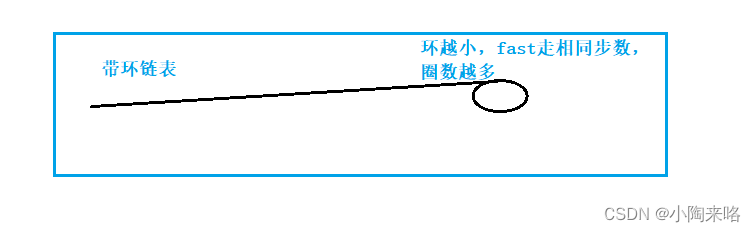
所以快指针走的总距离为
L+M+nC (n至少为1)*
n为走过的圈数

Ⅲ.总结归纳

因为快慢指针之间存在着关系，所以我们可以列出一个表达式，也就是快指针走的距离是慢指针走的距离的2倍
2*(L+M)=L+M+n*C

所以L=n*C-M
当最好情况下n=1时，L=C-M
L是什么？L就是开始点到入口点的距离
C-M是什么？C-M就是相遇点到入口点的距离。

也就是：一个指针从链表的起始位置开始运行，一个指针从相遇点位置绕环，每次都走一步，两个指针最终会在入口点的位置相遇

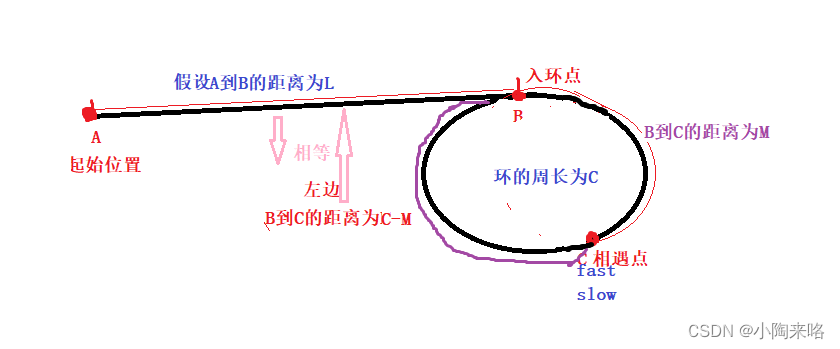
结论：带环定理

让一个指针从链表的起始位置开始遍历，同时让一个指针从带环的相遇点位置开始遍历，两个指针都是每次走一步，最终一定会在入环处相遇！

Ⅳ.带环链表真题

给定一个链表，返回链表开始入环的第一个结点，如果链表无环，则返回NULL

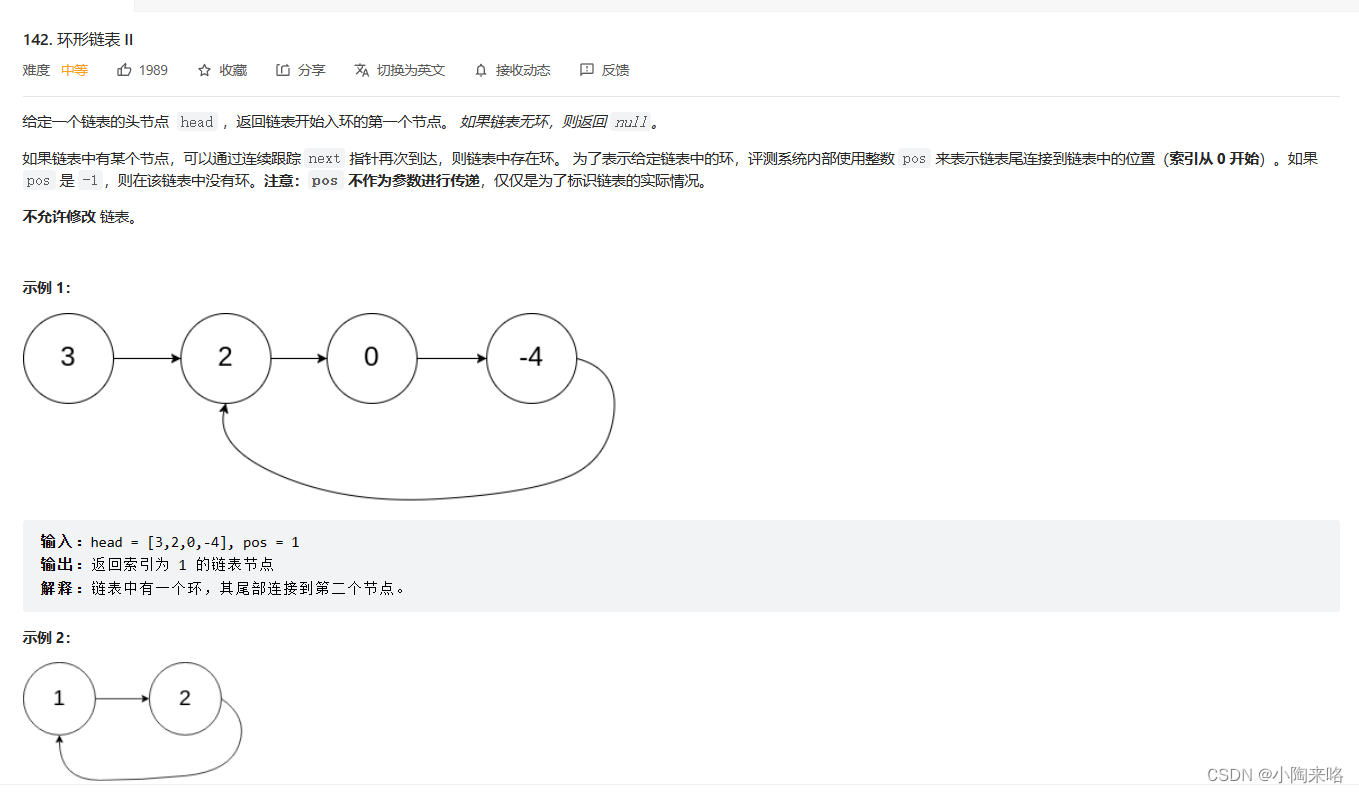
《链表带环问题Ⅱ》
要求判断是否有环，如果有请返回入环的第一个结点。

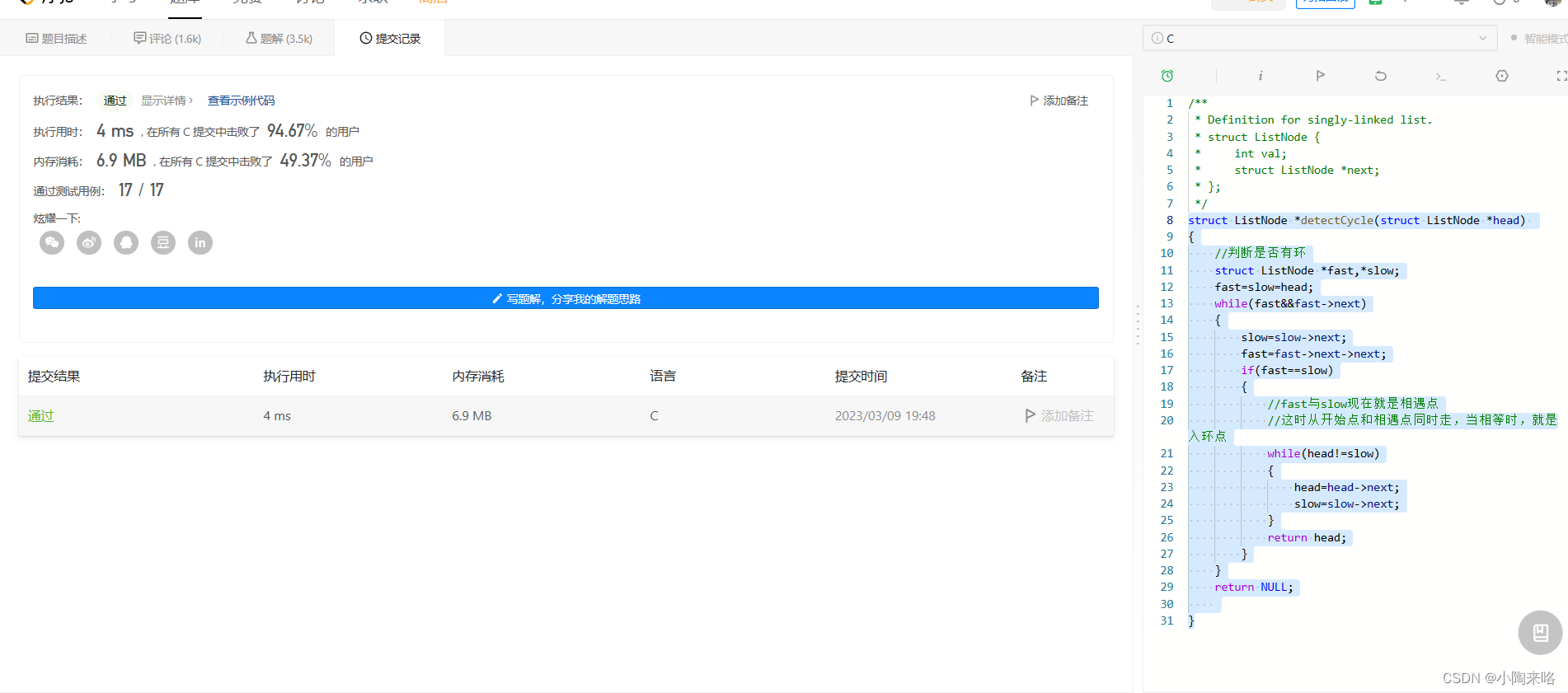
方法1：利用带环定理

这就是我上面两个例子的结合，第一步判断是否有环，第二步利用上面的定理：在有环的链表中，从开始位置和相遇点同时出发，将会在入环点相遇。

struct ListNode *detectCycle(struct ListNode *head) 
{
    //首先判断是否有环
    struct ListNode *fast,*slow;
    fast=slow=head;
    while(fast&&fast->next)
    {
        slow=slow->next;
        fast=fast->next->next;
        if(fast==slow)
        {
            //fast与slow现在就是相遇点
            //这时从开始点和相遇点同时走，当相等时，就是入环点
            while(head!=slow)//如果不相同就一直走
            {
                head=head->next;
                slow=slow->next;
            }
            return head;//当跳出来时就是入环点
        }
    }
    return NULL;
    
}

方法2：转换为相交链表问题

还有一种方法可以快速解决这个问题，我们可以将相遇点与后面那个结点断开

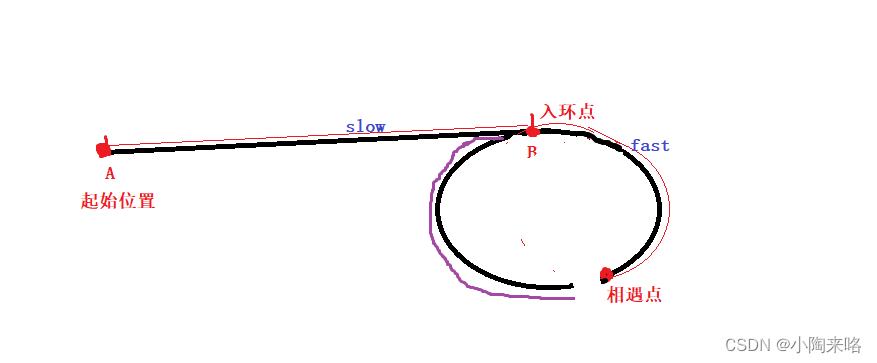
那从断开的结点开始是不是就相当于一个链表了，那这道题目就转变成了相交链表的问题了，求两个链表相交的结点问题，我在上一篇博客中有写过这种方法。
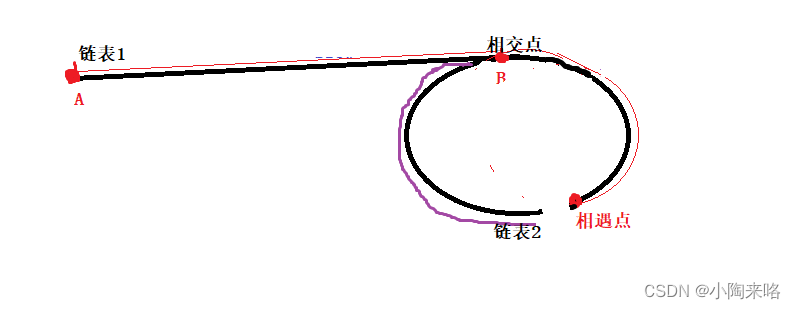
如果求两个相交链表的结点呢？
其实很简单：
第一步求出两个链表的长度
第二步让长度较长的链表先走长度差步
第三两个链表一起走，并进行比较，当两个链表的结点相同时就是相交结点。

struct ListNode *detectCycle(struct ListNode *head)
 {
  //首先要找到相遇点，才能断开它
  struct ListNode*fast,*slow;
  fast=slow=head;
  while(fast&&fast->next)
  {
      slow=slow->next;
      fast=fast->next->next;
      if(fast==slow)
      {
          //fast和slow现在就是相遇点，断开它和下一个结点并保存下一个结点的地址
          struct ListNode*newnode=slow->next;
          slow->next=NULL;
          //newnode就是新链表的头指针啦
    //开始求两个链表长度！
    int len1=0,len2=0;
    struct ListNode*tail1=head,*tail2=newnode;
    while(tail1)//计算链表1的长度
    {
        tail1=tail1->next;
        ++len1;
    }
    while(tail2)//计算链表2的长度
    {
        tail2=tail2->next;
        ++len2;
    }
    //两个链表长度是求出来来了，但不知道哪个是长链表哪个是短链表呀，所以还需要讨论下
    int gap=abs(len1-len2);
    struct ListNode*longlist=head,*shortlist=newnode;
    if(len1<len2)
    {
        longlist=newnode;
        shortlist=head;
    }
    //让长的链表先走长度差
    while(gap--)
    {
        longlist=longlist->next;
    }
    //然后两个链表再一起走，比较相同的时就是相交结点
    while(longlist!=shortlist)
    {
       longlist=longlist->next;
       shortlist=shortlist->next;
    }
    return longlist;//最后返回相交结点
      }
  }  
  return NULL;
}