文章目录
- 引言
- I 几何学中的古典难题(几何作图题)
-
- 1.1 伽罗瓦
- 1.2 伽罗瓦理论
- II 数学难题的启发
-
- 2.1 跳出圈外
- 2.2 工具的作用
引言
毕达哥拉斯定理做保障:任何自然数的平方根都可以用圆规和直尺作出来
高斯用直尺和圆规作图解决正十七边形画法的问题,正十七边形的边长计算出来只有平方根。
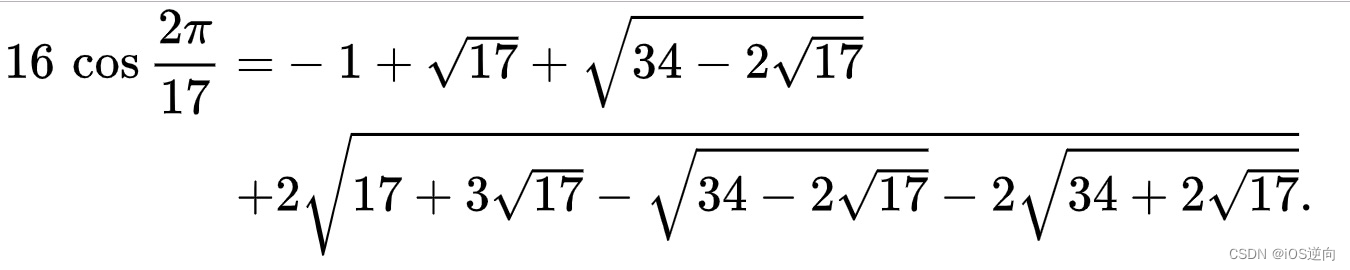
I 几何学中的古典难题(几何作图题)
用圆规和直尺做立方根无理数的问题:它其实不是一个在欧几里得几何范围内能够解决的问题,它们都是代数题。
- 三等分任意的已知角,等价于算出1/3个角的任何一种三角函数,它的解析解包含了立方根。
- 倍立方问题:做一个体积是已知立方体两倍的立方体
- 方圆问题: 做一个面积等于已知正方形的圆,或者反过来。
1.1 伽罗瓦
生于1811年,死于1832年。在1846年,法