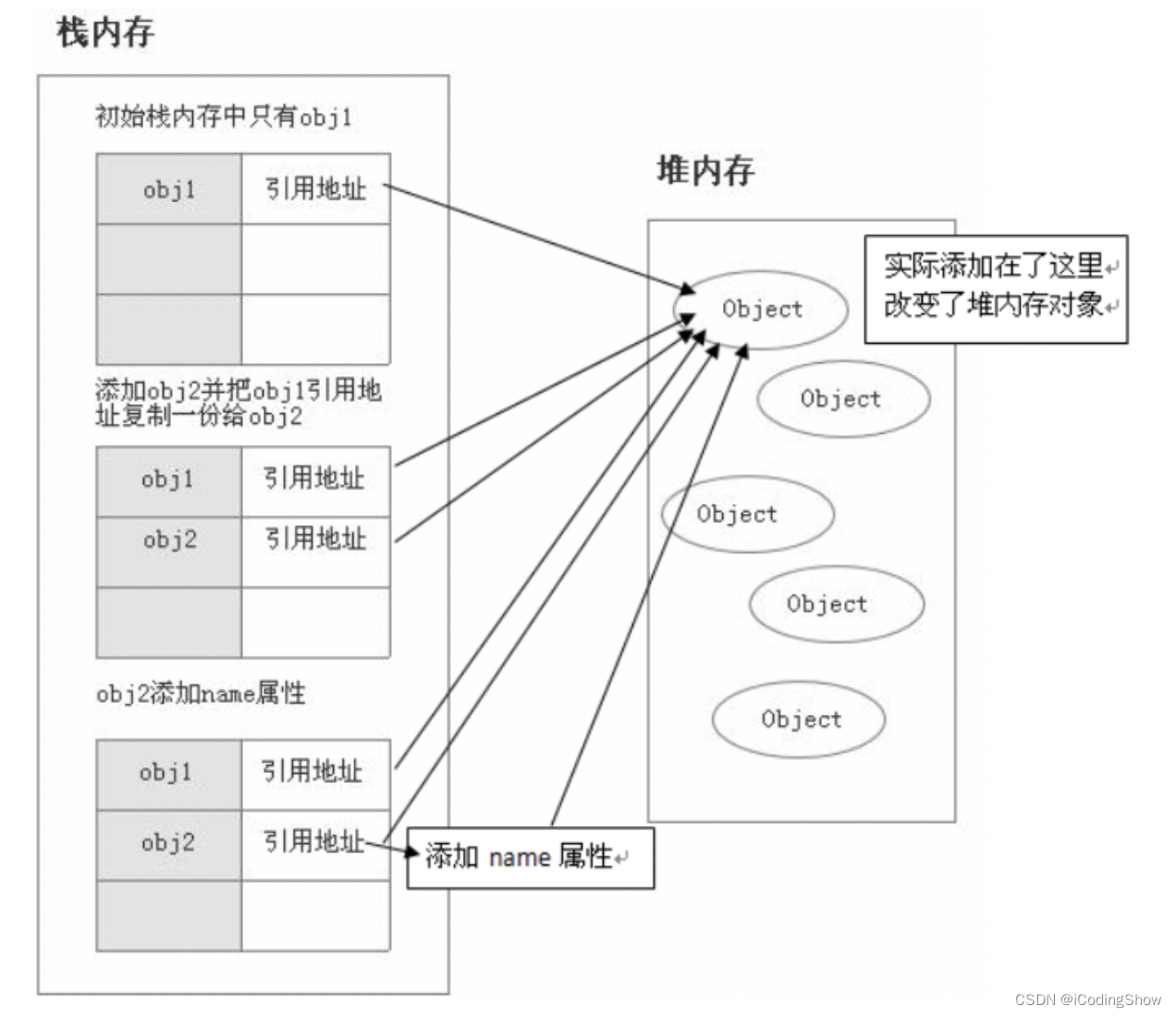
基础入门
图像与信号
图像
图像是人对视觉感知的物质再现。图像可以由光学设备获取,也可以人为创作。随着数字采集技术和信号处理理论的发展,越来越多的图像以数字形式存储。因而,有些情况下”图像“一词实际上是指数字图像。图像相关的话题包括图像采集、图像制作、图像分析和图像处理等。图像分为静态影像和动态影像。图像时一种视觉信号。透过专业设计的图像,可以发展成人与人沟通的视觉语言,也可以是了解族群文化与历史源流的史料。世界美术史中大量的平面绘画、;体雕塑与建筑,也可视为人类由古自今文明发展的图像文化资产。
信号
在信息论中,信号是一种信息流。我们感兴趣的大部分信号都可表述为时间或位置的函数。任何携带信息的物理量皆可以作为信号。信号本身所携带的信息是我们的目的,从中提取有需要有用的信号,抑制干扰部分的信号处理的目标。所有维度上均连续的信号是模拟信号,所有维度上均离散的信号是数学信号。数学信号是通过模拟信号时间、幅度维度上离散化产生的。
数字图像信号表示与分类
二值图像
图像中每个像素的亮度值仅可以取自0或1的图像,因此也称为1-bit图像。二值化图像仅包含两个信号值的图像,该信号更多使用于表示图像的形状和轮廓。
灰度图像
也称为灰阶图像。图像中每个像素可以由0(黑)到255(白)的亮度值表示。0-255之间表示不同的灰度级。当彩色图(如RGB)的颜色信号相等时,如R=G=B,图像呈现出黑色到白色的过度行为。往往用于表示图像的颜色深浅性。类似于绘画中的素描
彩色图像
彩色图像主要分为两种类型,RGB及CMYK。其中RGB的彩色图像是由三种不同颜色成分组合而成,一个为红色,一个为绿色,一个为蓝色。而CMYK类型的图像则由四个颜色成分组成:青C、品M、黄Y、黑K。CMYK类型的图像主要用于印刷行业。全彩是指影像中的物体颜色和人类肉眼所见的颜色非常相似。在黑白影像中全彩则是物体的明亮程度。但因为颜色染料等媒体的化学性质和人类肉眼不同,因此不可能得到绝对的全彩。在假色影像中物体的色彩和影像的颜色则改变了,这可能在很多地方出现。例如负片的颜色就可以被叫做假色,因为负片的颜色是物体颜色的补色。但假色常被用于表示电磁波谱中不可见光的部分。诸如遥感和宇宙光谱。
假彩色图像
多光谱图像
立体图像
立体图像是一物体由不同角度拍摄的一对图像,通常情况下我们可以用立体图像计算出图像的深度信息。立体图像即在平面上添加深度光影信息,视觉效果(使图像看起来)像是”立体”立体图像时视觉结果,而三维图像则是信息描述。
三维图像
三维图像是由一组堆栈的二位图像组成。每一幅图像表示物体的一个二维面
图像属性之像素
像素信息
像素,为影像显示的基本单位,译为英文“pixel”,pix是英文单词picture的常用简写,加上英语单词“元素”element,得到pixel,故“像素”表示“画像元素”之意,有时亦被称为pel。每个这样的消息元素不是一个点或者一个方块,而是一个抽象的取样。
从显示器看图像表示
显示器最常见的表示方式为xx英寸,而表示显示器的核心参数为PPI,为每英寸像素,也称为像素密度,所以,点并不是图像的表示!
LDPI 低等像素密度 每英寸大约120像素(36 x 36 px)
MDPI 中等像素密度 每英寸大约160像素(48 x 48 px)
HDPI 高等像素密度 每英寸大约240像素 (72 x 72 px)
XHDPI 极高等像素密度 每英寸大约320像素 (96 x 96 px)
XXHDPI 超高等像素密度 每英寸大约480像素 (144 x 144 px)
位图
位图(英语:Bitmap, 台湾称为点阵图),又称为栅格图(Raster graphics),是使用像素阵列来表示的图像。
每个像素使用的信息位数越多,可用的颜色就越多,颜色表现就越逼真,相应的数据量越大。
矢量图
矢量图形是计算机图形学中用点、直线或者多边形等基于数学方程的几何图元表示的图像。所有的现代计算机显示器都要将矢量图形转换成栅格图像的格式,包含屏幕上每个像素数值的栅格图像保存在内存中。
图像属性之颜色
人眼视觉系统
人眼的视网膜上,发布着两种感光细胞:视杆细胞和视锥细胞
视杆细胞:主要在暗光情况下发挥作用,没有色彩识别功能,所以我们在光线昏暗的条件下,分辨不出颜色。
视锥细胞:在明亮条件下发挥作用。正常情况下,人眼视网膜上存在能感应红(R)、绿(G)、蓝(B)的三种视锥细胞,S主要分辨短波,主要蓝色,M,中波,主要绿色,L长波,主要红色。
N色视者–拥有N中视锥细胞的动物或者人
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-bVWJ52xZ-1678179718427)(C:\Users\86166\AppData\Roaming\Typora\typora-user-images\image-20211220212202851.png)]](https://img-blog.csdnimg.cn/842314b0b14543a4b9f437b95a369ee3.png)
皮皮虾拥有16种视锥细胞,他们看到的颜色种类是人类的10倍之多,赶超地球上所有的动物。它们能够看到紫外线、红外线,甚至于偏振光。
颜色与模型
GRB模型
和主要的人视觉系统匹配的模型,以三原色建立
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-GP3nyyNI-1678179718428)(C:\Users\86166\AppData\Roaming\Typora\typora-user-images\image-20211220213311152.png)]](https://img-blog.csdnimg.cn/47ebfa309284402ba972a6876ecef781.png)
HSV模型
HSV是色度(Hue)、饱和度(Saturation)和亮度(Value)的简写,该模型通过这三个特性对颜色进行描述。
HSV(色相饱和度值),HSI(色相饱和度强度)和HSL(色相饱和度亮度)是RGB颜色模型中点的三种最常见的圆柱坐标表示。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-alHkuODd-1678179718429)(C:\Users\86166\AppData\Roaming\Typora\typora-user-images\image-20211220213558708.png)]](https://img-blog.csdnimg.cn/b276ca61cf0e48fa97945d4fe3f19e55.png)
Lab模型
是一种设备无光的颜色模型,是一种基于生理特征的颜色模型
Lab颜色空间中的L分量用于表示像素的亮度,取值范围是[0,100],表示从纯黑到纯白;a表示从红色到绿色的范围,取值范围是[127,-128];b表示从黄色到蓝色的范围,取值范围是[127,-128]。
RGB颜色空间不能直接转换为Lab颜色空间,需要借助XYZ颜色空间,把RGB颜色空间转换到XYZ颜色空间,之后再把XYZ颜色转换到Lab颜色空间。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-daxY8o6B-1678179718429)(C:\Users\86166\AppData\Roaming\Typora\typora-user-images\image-20211220214131250.png)]](https://img-blog.csdnimg.cn/73567eed1a184a4aa135de3c99f8f575.png)
YUV模型
YUV模型是电视信号系统所采用的颜色编码方式。这三个变量分别表示是像素的亮度(Y)以及红色分量与亮度的信号差值(U)和蓝色与亮度的差值(V)
黑白视频只有Y(Luma,Luminance)视频,也就是灰阶值。到了彩色电视规格的指定,是以YUV/YIQ的格式来处理彩色电视图像,把UV视作表示彩度的C(Chrominance或Chroma),如果忽略C信号,那么剩下的Y(Luma)信号就跟之前的黑白电视频号相同,这样一来便解决彩色电视机与黑白电视机的兼容问题。Y’UV最大的优点在于只需占用极少的带宽。
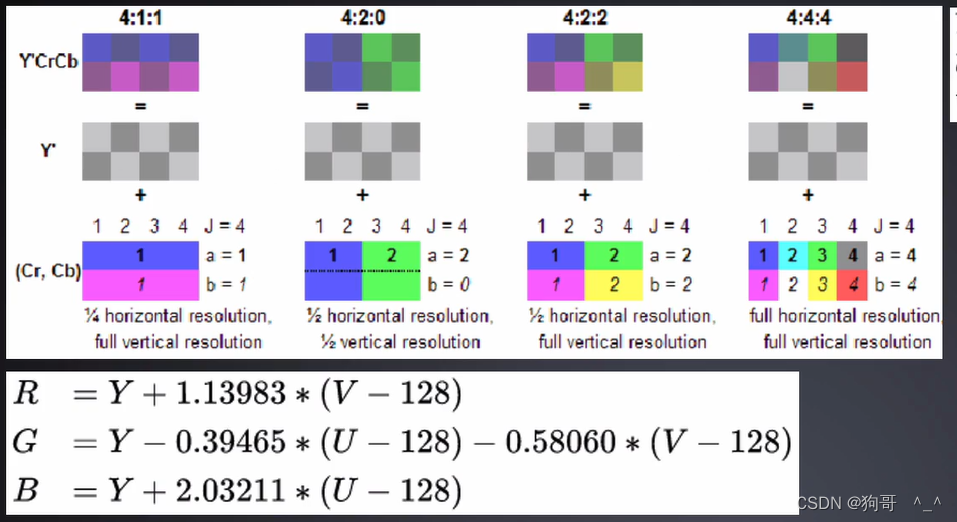
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-FoedbsmQ-1678179718430)(C:\Users\86166\AppData\Roaming\Typora\typora-user-images\image-20211220214620618.png)]](https://img-blog.csdnimg.cn/13576b5e332548dbb21260cdc9f990de.png)
GRAY模型
GRAY模型并不是一个彩色模型,他是一个灰度图像的模型,其命名使用的是英文单词gray的全字母大写。
灰度图像只有单通道,灰度值根据图像位数不同由0到最大依次表示由黑到白,例如8UC1格式,由黑到白被量化成了256个等级,通过0-255表示,其中255表示白色
Gray = R* 0.299 + G * 0.587 + B * 0.114
其实这个公式就是YUV里的Y算法
CMYK模型
印刷四分色模式(CMYK)是彩色印刷时采用的一种套色模式,利用色料的三原色混色原理,加上黑色油墨,共计四种颜色混合叠加,形成所谓全彩印刷
C:Cyan= 青色,常被误称“天蓝色”或“湛蓝”
M:Magenta = 洋红色,又称为“品红色”
Y:Yellow = 黄色
K:black = 黑色,(避免和RGB里的B混肴,故使用K)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-51xqNirG-1678179718431)(C:\Users\86166\AppData\Roaming\Typora\typora-user-images\image-20211220215745534.png)]](https://img-blog.csdnimg.cn/4af880cdcb2f4e99aeb8a8dbcaa95b15.png)
其他专业名词:
色光:光谱当中的带来的颜色,其实就是指RGB模型
色料:绘画要用的颜色,一般指CMYK模型内的
色调:将明度和彩度合为色调。如下图:【红】是色相,而【鲜、浅、粉】即是色调
图像的格式详解
图片格式比较
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-fCG8Ee1V-1678179718431)(C:\Users\86166\AppData\Roaming\Typora\typora-user-images\image-20211220224330898.png)]](https://img-blog.csdnimg.cn/3a93fd7a85db4031bc818219f9465ad9.png)
常见图片格式bmp
BMP是(Windows位图)Windows位图可以用任何颜色深度(从黑白到24位颜色)存储单个光栅图像。Windows位图文件格式与其他Microsoft Windows程序兼容。它不支持文件压缩,也不适用于Web页。从总体上看,Windows位图文件格式的缺点超过了它的优点。为了保证照片图像的质量,请使用PNG、JPEG、TIFF文件。BMP文件适用于Windows的墙纸。
优点:BMP支持1位到24位颜色深度。
BMP格式与现有Windows程序(尤其是较旧的程序)广泛兼容
缺点:BMP不支持压缩,这会造成文件非常大。
常见图片格式JPEG(.jpg .jpeg)
是一种有损压缩格式,能够将图像压缩在很小的存储的空间,图像中重复或不重要的资料会被丢失,因此容易造成图像数据的损伤。尤其是使用过高的压缩比例,将使最终解压后恢复的图像质量明显降低,如果追求高品质图像,不宜采用过高压缩比例。
优点:
摄影作品或写实作品支持高级压缩。
利用可变的压缩比可以控制文件的大小。
支持交错(对应渐进式JPEG文件)。
JPEG广泛支持Internet标准。
缺点:
有损耗压缩会使原始图片数据质量下降。
当您编辑和重新保存JPEG文件时,JPEG会混合原始图片数据的质量下降。这种下降是积累性的。
JPEG不适用于所含颜色很少、具有大块颜色相近的区域或亮度差异十分明显的较简单的图片。
png格式
便携式网络图形(外语简称PNG、外语全称:Portable Network Graphics),是网上接受的最新图像文件格式。PNG能够提供长度比GIF小30%的无损压缩图像文件。它同时提供24位和48位真彩色图像支持以及其他诸多技术性支持。
优先:
PNG支持高级别无损耗压缩。
PNG支持alpha通道透明度。
PNG支持伽玛校正。
PNG支持交错。
PNG受最新的Web浏览器支持。
缺点:
较旧的浏览器和程序可能不支持PNG支持。
作为Internal文件格式,与JPEG的有损耗压缩相比,PNG提供的压缩量较少。
作为Internal文件格式,PNG对多图像文件或动画文件不提供任何支持。GIF格式支持多图像文件和动画支持。
Mat类与基础函数
开源框架学习办法与Mat类整体分析
如果进行开源框架的学习
整体:
(1)开源框架的作用是什么?
1、可以应用在什么方面
2、整体的结构是什么?
(2)怎么使用该开源框架
1、使用开源框架的公开案例
2、以OpenCV举例:
有哪些类
有哪些办法
(3)理解开源框架的设计逻辑
1、以OpneCV举例
有哪些模块、各模块作用是什么,各模块是怎么联系到一起的
2、看源代码进行分析
细节(以Mat类举例)
(1)从模块意义上分析
Mat->matrix 矩阵
[1,1]
容器->存放数据的容器
存放图像信息
图像:
二值图
彩图
数据图
(2)从语言意义上分析
类:
属性:
行,列,数据,维数
图像的种类
办法:
矩阵运算方式,获取/设置属性的办法
不同种类的图像设置方式
构造函数/析构函数········
内存管理方式:
(1)无内存管理,纯靠系统
(2)手动管理方式,纯靠程序员设计代码
(3)GC管理,垃圾收集,定时或定间隔,将不需要的空间进行回收
(4)引用计数式管理,RC,如果有新的引用,引用计数+1,如果旧的引用消失,引用计数-1。引用计数降为0,则会进行内存的回收,OpenCV的对象采取就是这种方式
(5)内存池式管理。类似于鱼缸式的管理,这种方式一般情况下是作为辅助管理方式,或整体管理方式。
源代码怎么看
(1)针对于c语言
函数是c语言的模块划分方式,重点就是分析各函数的实现方式
(2)针对C++
模块
类
属性成员变量
办法 函数:
(1)属性
(2)办法
(3)内存管理方式
Mat类的内存和办法
#include <opencv2/opencv.hpp>
using namespace cv;
#include <iostream>
using namespace std;
void printMat(Mat &mat) {
cout << "Mat:" << mat << endl;
cout << "flags:" << mat.flags << endl;
cout << "dims:" << mat.dims << endl;
cout << "rows:" << mat.rows << "cols:" << mat.cols << endl;
if (mat.data)
{
cout << "data:存在" << endl;
}
cout << "存储相关:" << endl;
cout << "umatadata:" << mat.u << endl;
if (mat.u->refcount){
cout << "refcount:" << mat.u->refcount << endl;
}
}
int main(int argc, char const *argv[])
{
//仅创建对应的矩阵头信息,没有包含真正的矩阵内部数据
Mat m;
//CV_8UC1 8指数据位数,U指是否带符号,Cchannel信道数,1一个信道
Mat m_size(10, 10, CV_8UC1);
//zeros进行元素数据清零操作
m_size.zeros(10, 10, CV_8UC1);
imshow("test", m_size);
printMat(m_size);
m = m_size;
printMat(m);
Mat m1 = m;
printMat(m1);
//上述两种方式,都是浅拷贝,只会增加对应的引用计数(refcount),而不会产生新的内存
Mat mat_clone = m.clone();
Mat mat_copy_to_mat;
m.copyTo(mat_copy_to_mat);
printMat(mat_clone);
printMat(mat_copy_to_mat);
//上述两种方式,是深拷贝,会产生新的内存,对应的引用计数不会增加
Mat scalar_mat(100, 100, CV_8UC3, Scalar(128, 255, 0));
imshow("scalar", scalar_mat);
//获取对角线上的数据
cout << scalar_mat.diag(0) << endl;
//create 办法,进行数据的填充处理了,create之前的对象就被销毁了
Mat un_create;
printMat(un_create);
un_create.create(10, 10, CV_8UC1);
printMat(un_create);
//waitKey(0);
//Mat作用:
//(1)用于数学上的矩阵运算(2)进行图像数据的存储和相关的运算操作
return 0;
}
图片处理基本办法
#include <opencv2/opencv.hpp>
using namespace cv;
#include <iostream>
using namespace std;
int trackbarvalue;
Mat image;
void trackbarcallback(int value, void *data) {
cout << value << endl;
image &= 1;
image *= (value / 255.0);
imshow("window_name", image);
}
void mouseEvenCallBack(int event, int x, int y, int falg, void *userdata) {
cout << event << endl;
cout << x << ":" << y << endl;
}
int main(int argc, char const *argv[])
{
/*
图像存取相关函数
*/
//(1)图片的绝对路径或相对路径(2)读入图片到Mat容器当中的存取方式
Mat srcImage = imread("../spand.jpg", IMREAD_GRAYSCALE);
image = srcImage;
//autosize 在部分环境下,可能无法改变窗口的大小 normal可以改变
namedWindow("window_name", WINDOW_NORMAL);
//添加进度条,注意使用回调函数
createTrackbar("trackbar", "window_name", &trackbarvalue, 255, trackbarcallback);
//鼠标的操作
setMouseCallback("window_name", mouseEvenCallBack, (void *)&srcImage);
//(1)显示的图片名称(2)图片的容器
imshow("window_name", srcImage);
/*
1、保存的图片名称,注意需要带后缀名
2、保存的源图片容器
3、存储过程中的编码处理 比如压缩处理
*/
vector<int> comparession;
comparession.push_back(IMWRITE_PNG_COMPRESSION);
comparession.push_back(9);
imwrite("gray_logo1.jpg", srcImage, comparession);
//键盘组操作 等待一个任意字符,参数为延迟时间
waitKey(0);
return 0;
}
绘制方法
#include <opencv2/opencv.hpp>
using namespace cv;
#include <iostream>
using namespace std;
int main(int argc, char const *argv[])
{
/*
1、线Line
2、矩形rectangle
3、圆circle
4、椭圆ellipse
5、多边形 poly
*/
/*
1、Point 点x,y
2、Size 尺寸 width height
3、Rect 矩形 x,y,width,height
4、Scalar 颜色
*/
Mat m(600, 400, CV_8UC4);
m.zeros(600, 400, CV_8UC4);
/*
Scalar 颜色对象,可以填写对应的颜色
thickness 线的宽度 对于包围图形,-1代表填充内部空间
Linettype 线的类型
*/
line(m, Point(100, 100), Point(300, 500), Scalar(0, 0, 255, 128), 5, -1);
rectangle(m, Point(100, 100), Point(300, 500), Scalar(0, 255, 0, 128), -1, LINE_4);
circle(m, Point(100, 100), 50, Scalar(255, 0, 0, 128), -1, LINE_4);
/*
cvtColor
*/
cvtColor(m, m, COLOR_BGR2BGRA, 4);
/*
如果是单信道channel,单独数值
如果是多信道呢?
*/
uchar signal_channel = m.at<uchar>(100, 100);
Vec2b double_channel = m.at<Vec2d>(100, 100);
imshow("result", m);
waitKey(0);
return 0;
}
图形处理技术
图像灰度变换技术
灰度变换技术主要应用有两个方面
(1)针对图像轮廓处理,提取关键信息
(2)进行细节优化,提升图像的效果
常用灰度变换技术
(1)阈值化处理
(2)直方涂信息处理
(3)灰度变换函数
线性代数
对数变换
Gamma校正
综合使用(对比度拉伸技术 灰度分层 比特平面分层)
(4)距离变换
阈值处理
阈值处理即图像处理二值化。是图像分割的一种最简单的办法。二值化可以把灰度图像转换成二值图像。把大于某个临界灰度值的像素灰度设为灰度极大值,把小于这个值的像素灰度设为灰度极小值,从而实现二值化。
常用阈值处理:
OTSU阈值化处理
固定阈值化
自适化阈值化
双阈值化
半阈值化
OTSU阈值化处理
OTSU算法也称最大类间差法,有时也称之为大津算法,由大津于1979年提出,被认为是图像分割中阈值选取的最佳算法,
它的基本思想是,用一个阈值将图像中的数据分为两类,一类中图像的像素点的灰度均小于这个阈值,另一类中的图像的像素点的灰度均大于或者等于该阈值。则利用该阈值可以将图像分为前景和背景两个部分。一般情况下,提取前景便可以得到我们想要的图像轮廓。
#include <opencv2/opencv.hpp>
using namespace cv;
#include <iostream>
using namespace std;
//阈值计算
int my_otsu(Mat inputImg) {
//初始化
int rows = inputImg.rows;
int cols = inputImg.cols;
int sumPixel[256] = {0};
float proDis[256] = {0};
int result_threshold;
//拿到灰度值的统计信息,统计一张图中的各个像素的出现的灰度值次数,比如在点(2,3)处的灰度值为100,而(20,20)处的灰度值也是100,那么就统计100出现两次
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
sumPixel[(int)inputImg.at<uchar>(i, j)]++;
//cout << i << ":" << j << "->" << (int)inputImg.at<uchar>(i, j) << endl;
}
}
//计算概率发布,某灰度值出现的次数占所有图所有像素的比例
for (int i = 0; i < 256; i++) {
proDis[i] = sumPixel[i] / (float)(rows * cols);
}
//计算最大方差
float all_left, all_right, avg_left, avg_right, temp_left, temp_right, temp_delta;
float max_delta = 0.0;
for (int i = 0; i < 255; i++) {
all_left = all_right = avg_left = avg_right = temp_left = temp_right = temp_delta = 0;
for (int j = 0; j < 255; j++) {//把所有的灰度值分为左右两部分
if (j <= i) {
all_left += proDis[j];
temp_left += j * proDis[j];
} else {
all_right += proDis[j];
temp_right += j * proDis[j];
}
}
//通过求出的左右两部分的所有占比然后就求平均值
avg_left = temp_left / all_left;
avg_right = temp_right / all_right;
//求方差
temp_delta = (float)(all_left * all_right * pow((avg_left - avg_right), 2));
if (temp_delta > max_delta) {
max_delta = temp_delta;
result_threshold = i;
}
}
//计算结果
return result_threshold;
}
int main(int argc, char const *argv[])
{
//读入图片
Mat srcImg = imread("A:/OPENC/threshold/R-C.jpg");
//转换为灰度图
Mat grayImg;
cvtColor(srcImg, grayImg, COLOR_RGB2GRAY);
// imshow("src", srcImg);
// imshow("gray", grayImg);
//进行阈值计算
int otsu = my_otsu(grayImg);
cout << otsu << endl;
//通过阈值进行二值化
Mat result = grayImg.clone();
//OTSU阈值化处理
for (int i = 0; i < grayImg.rows; i++) {
for (int j = 0; j < grayImg.cols; j++) {
if (grayImg.at<uchar>(i , j) >= otsu) {
result.at<uchar>(i, j) = 255;
} else {
result.at<uchar>(i, j) = 0;
}
}
}
imshow("result", result);
//
waitKey(0);
return 0;
}
固定阈值化
阈值计算函数与办法
#include <opencv2/opencv.hpp>
using namespace cv;
#include <iostream>
using namespace std;
int main(int argc, char const *argv[])
{
Mat srcImg = imread("A:/OPENC/threshold/R-C.jpg", IMREAD_GRAYSCALE);
//根据填写阈值进行处理,根据输入的type类型阈值处理
Mat resultImg;
threshold(srcImg, resultImg, 138, 255, THRESH_BINARY);
// THRESH_BINARY = 0 二值化,超过阈值,保留为白色
// THRESH_BINARY_INV = 1 反二值化,与上面的方式相反
// THRESH_TRUNC = 2 超过阈值的部分,保留到阈值
// THRESH_TOZERO = 3 不足阈值的部分,清0,超过阈值的部分,保留
// THRESH_TOZERO_INV = 4 不足阈值保留,超过,清0
//THRESH_MASK = 7 一般用在抠图或则截取信息
//THRESH_OTSU = 8 是否使用OTSU算法
//THRESH_TRIANGLE = 16
imshow("src", srcImg);
imshow("gray", resultImg);
waitKey(0);
return 0;
}
自适应阈值化
Mat adapImg;
/*
ADAPTIVE_THRESH_MEAN_C 平均计算
ADAPTIVE_THRESH_GAUSSIAN_C 高斯算法, 计算当前值距离,通过高斯方程拿到结果
*/
adaptiveThreshold(srcImg, adapImg, 255, ADAPTIVE_THRESH_MEAN_C, THRESH_BINARY, 5, 2);
双阈值化
半阈值化
/*
固定阈值,进行全局阈值处理,针对亮暗区分明显的使用办法
自适应阈值,前后区分不明显,获取轮廓的方式
双阈值化,通过大小阈值的两次操作,找到图片中的关键信息
半阈值化,主要用于拿到图片中的诸如文字特征明显的信息
*/
直方图信息处理
在统计学中,直方图是一种对数据发布情况的图形表示,是一种二维统计图表,它的两个坐标分别是统计样本和该样本对应的某个属性的度量,以长条图的形式具体表现。因为直方图的长度及宽度很适合用来表现数量上的变化,所以较容易解读差异小的数值
直方图是可以对整幅图的灰度发布进行整体了解图示,通过直方图我们可以对图像的对比度、亮度和灰度发布等有一个直观了解。
实现直方图显示图片像素:
#include <opencv2/opencv.hpp>
using namespace cv;
#include <iostream>
using namespace std;
int main(int argc, char const *argv[])
{
//灰度直方图 H-S直方图 RGB直方图
Mat srcImg = imread("A:/OPENC/histogram/zhanyangsong.jpg");
Mat grayImg;
cvtColor(srcImg, grayImg, COLOR_RGB2GRAY);
//计算直方图信息
/*
CV_EXPORTS void calcHist( const Mat* images, int nimages,
const int* channels, InputArray mask,
OutputArray hist, int dims, const int* histSize,
const float** ranges, bool uniform = true, bool accumulate = false );
images 输入的图片组:图片需要拥有相同的大小,相同的颜色深度
nimages 图像的个数
channels 需要计算的直方图的通道个数
mask 可选的掩码,一般不使用时设置为空。掩码图片必须和输入的图片组大小相同。
hist 输出的直方图信息
dima 直方图的维数
histSize 直方图维度大小
ranges 直方图统计的范围
uniform 是否进行归一化处理
accumulate 累计操作,默认不需要
*/
int channels[1] = {0};
Mat hist;
int histSize[1] = {256};
float hrange[2] = {0, 255};
const float *ranges[1] = {hrange};
calcHist(&grayImg, 1, channels, Mat(), hist, 1, histSize, ranges);
//绘制直方图
Mat histOutputImg(256, 256, CV_8U, Scalar(255));
double maxValue;
double minValue;
minMaxLoc(hist, &minValue, &maxValue);
int hpt = 0.9 * 256;
for (int i = 0; i < 256; i++) {
float binVal = hist.at<float>(i);
int temp = (binVal * hpt / maxValue);
line(histOutputImg, Point(i, 256), Point(i, 256 - temp), Scalar::all(0));
}
imshow("srcImg", srcImg);
imshow("grap", grayImg);
imshow("result", histOutputImg);
waitKey(0);
return 0;
}
常用直方图操作:
直方图均衡
直方图匹配
直方图对比
直方图查找
直方图累计
#include <opencv2/opencv.hpp>
using namespace cv;
#include <iostream>
#include <vector>
using namespace std;
Mat histOutputImg(Mat hist) {
Mat histOutputImg(256, 256, CV_8U, Scalar(255));
double maxValue;
double minValue;
minMaxLoc(hist, &minValue, &maxValue);
int hpt = 0.9 * 256;
for (int i = 0; i < 256; i++) {
float binVal = hist.at<float>(i);
int temp = (binVal * hpt / maxValue);
line(histOutputImg, Point(i, 256), Point(i, 256 - temp), Scalar::all(0));
}
return histOutputImg;
}
int main(int argc, char const *argv[])
{
//灰度直方图 H-S直方图 RGB直方图
Mat srcImg = imread("A:/OPENC/histogram/1.jpg");
Mat grayImg;
cvtColor(srcImg, grayImg, COLOR_RGB2GRAY);
//计算直方图信息
/*
CV_EXPORTS void calcHist( const Mat* images, int nimages,
const int* channels, InputArray mask,
OutputArray hist, int dims, const int* histSize,
const float** ranges, bool uniform = true, bool accumulate = false );
images 输入的图片组:图片需要拥有相同的大小,相同的颜色深度
nimages 图像的个数
channels 需要计算的直方图的通道个数
mask 可选的掩码,一般不使用时设置为空。掩码图片必须和输入的图片组大小相同。
hist 输出的直方图信息
dima 直方图的维数
histSize 直方图维度大小
ranges 直方图统计的范围
uniform 是否进行归一化处理
accumulate 累计操作,默认不需要
*/
int channels[1] = {0};
Mat hist;
int histSize[1] = {256};
float hrange[2] = {0, 255};
const float *ranges[1] = {hrange};
calcHist(&grayImg, 1, channels, Mat(), hist, 1, histSize, ranges);
//绘制直方图
//直方图均衡化 将过亮或过暗的图片通过均衡化,细节暴露出来
Mat equalizeOutImg;
equalizeHist(grayImg, equalizeOutImg);
Mat outHist;
calcHist(&grayImg, 1, channels, Mat(), outHist, 1, histSize, ranges);
//彩色图均衡化处理
Mat colorImg;
vector<Mat> BRG_channels;
split(srcImg, BRG_channels);
for (unsigned long i = 0; i < BRG_channels.size(); i++) {
equalizeHist(BRG_channels[i], BRG_channels[i]);
}
merge(BRG_channels, colorImg);
//直方图匹配:使两张匹配的图片的像素融合
Mat newSrcImg = imread("A:/OPENC/histogram/zhanyangsong.jpg");
Mat newGrayImg;
cvtColor(newSrcImg, newGrayImg, COLOR_RGB2GRAY);
Mat newHist;
calcHist(&newGrayImg, 1, channels, Mat(), newHist, 1, histSize, ranges);
//计算图片的累计概率
float histOld[256] = {hist.at<float>(0)};
float histNew[256] = {newHist.at<float>(0)};
for (int i = 0; i < 256; i++) {
histOld[i] = histOld[i - 1] + hist.at<float>(i);
histNew[i] = histNew[i - 1] + newHist.at<float>(i);
}
//构建累计概率误差概率
float diff[256][256];
for (int i = 0; i < 256; i++) {
for (int j = 0; j < 256; j++) {
diff[i][j] = fabs(histOld[i] - histNew[j]);
}
}
//生成LUT(lookuptable)表
Mat Lut(1, 256, CV_8U);
for (int i = 0; i < 256; i++) {
float min = diff[i][0];
int index = 0;
for (int j = 0; j < 256; j++) {
if (min > diff[i][j]) {
min = diff[i][j];
index = j;
}
}
Lut.at<uchar>(i) = (uchar)index;
}
Mat resultOutImg, histOut;
LUT(grayImg, Lut, resultOutImg);
calcHist(&resultOutImg, 1, channels, Mat(), histOut, 1, histSize, ranges);
//直方图对比
for (int i = 0; i < 6; i++) {
cout << compareHist(hist, newHist, i) << endl;
}
//imshow("srcImg", srcImg);
// imshow("grap", grayImg);
// imshow("histImg", histOutputImg(hist));
// imshow("result", histOutputImg(hist));
// imshow("equalineOutImg", equalizeOutImg);
//imshow("histImg", histOutputImg(outHist));
//imshow("ColorImg", colorImg);
// imshow("newSrcImg", newGrayImg);
// imshow("newHist", histOutputImg(newHist));
// imshow("outImg", resultOutImg);
// imshow("histout", histOutputImg(histOut));
waitKey(0);
return 0;
}
灰度处理函数及应用
线性变换
通过做线性变换改变单个像素点的值可以调节整幅图像的亮度和对比度,即对像素进行线性变换,令r为变换前的灰度,s为变换后的灰度,则线性变换的函数:
S = ar + b
其中,a为直线的斜率,b为在y轴的截距。选择不同的a,b值会有不同的效果:
a > 1,增加图像的对比度
a < 1,减小图像的对比度
a = 0, b != 0,图像变亮或变暗
a < 0且b = 0,图像的亮区域变暗,暗区域变亮
a = -1, b = 255, 图像亮度反转