题目:
小蓝要用七段码数码管来表示一种特殊的文字。
上图给出了七段码数码管的一个图示,数码管中一共有 77 段可以发光的二 极管,分别标记为 a,b,c,d,e,f,g。
小蓝要选择一部分二极管(至少要有一个)发光来表达字符。在设计字符 的表达时,要求所有发光的二极管是连成一片的。
例如:b 发光,其他二极管不发光可以用来表达一种字符。
例如 c 发光,其他二极管不发光可以用来表达一种字符。这种方案与上 一行的方案可以用来表示不同的字符,尽管看上去比较相似。
例如:a,b,c,d,e 发光,f,g 不发光可以用来表达一种字符。
例如:b,f 发光,其他二极管不发光则不能用来表达一种字符,因为发光 的二极管没有连成一片。
请问,小蓝可以用七段码数码管表达多少种不同的字符?
思路:
最开始考虑为以每条边为起始边,寻找长度为0-7的路径。但是发现代码写不出来,呜呜。
去看了一下题解,发现了一种更简单的思路,得到所有的子序列,逐个对子序列进行判断是否连接,如果连接则表示可以表达为一种字符。其中:itertools.combinations(list_name, x)这个函数,可以得到list_name中长度为x的序列。
代码:
import os
import sys
from itertools import combinations
# 请在此输入您的代码
date = {'a': ['b', 'f'], 'b': ['a', 'c', 'g'], 'c': ['b', 'd', 'g'], 'd': ['c', 'e'], 'e': ['d', 'f', 'g'], 'f': ['a', 'e', 'g'], 'g':['b', 'c', 'e', 'f']}
roads = []
for i in range(8):
for j in combinations(date.keys(), i): #返回长度为0-7的所有子序列
roads.append(j)
#print(roads[1])
for road in roads:
flag = True
for i in range(len(road)-1):
if road[i+1] not in date[road[i]]: # 判断连接的条件是,后一个字符在前一个字符映射的字典中
flag = False
continue
if flag == False:
roads.remove(road) #将不连接的序列删除
print(len(roads))题目:
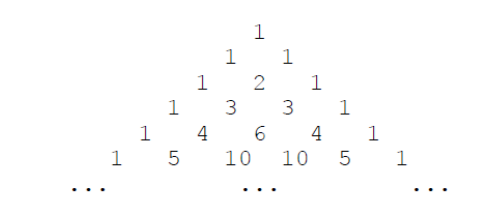
如果我们按从上到下、从左到右的顺序把所有数排成一列,可以得到如下数列: 1,1,1,1,2,1,1,3,3,1,1,4,6,4,1,⋯
给定一个正整数 N,请你输出数列中第一次出现 N 是在第几个数?
输入描述
输入一个整数 N。
输出描述
输出一个整数代表答案。
思路:
试图使用暴力,一个一个的创建杨辉三角,当前值为输入值时,停止创建并输出当前序列。提交后测试通过4个,呜呜。
看了题解,发现这个题目需要去找一个杨辉三角的规律,不仅是说某个数等于其肩上两个数之和。还有一些其他的规律,然后尝试根据该规律在某一斜行进行挨个查找,结果就是部分用例超时了。最后使用二分查找来提高效率。
参考:C++语言 分析 python 代码参考
代码:
import os
import sys
# 请在此输入您的代码
n = int(input())
date = [[0 for i in range(1000)] for i in range(1000)]
count = 0
flag = True
for i in range(1000):
if flag :
for j in range(i+1):
if i == 0 or j == i:
date[i][j] = 1
count += 1
else:
date[i][j] = date[i-1][j-1] + date[i-1][j]
count += 1
if date[i][j] == n:
flag = False
print(count)
break
else:
break
import os
import sys
# 请在此输入您的代码
n = int(input())
def C(a, b): # 计算C(a, b) a为上限,b为下限
res = 1
while a > 0:
res *= b/a
a -= 1
b -= 1
return res
for i in range(16, -1, -1):
flag = True
low = 2*i # 起始下限 也就是对称轴位置的元素
high = n # 这里说是终点下限 其实不懂为啥下限是n
while low <= high and flag:
mid = low + (high - low) // 2
val = C(i , mid)
if val > n:
high = mid - 1
elif val < n:
low = mid + 1
else:
flag = False
print(int((mid + 1) * mid / 2) + i + 1) # 这里最开始是对整个公式进行int(),会有两个用例测试不通过,看见有博主说是因为精度问题 只将前部分进行int()转换,就能全部通过啦
if flag == False:
break
Tips:
遇到题目,要学会去找其中的数学规律,这是很重要的!
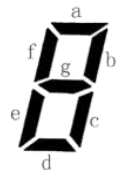






![[MySQL核心]1.表操作](https://img-blog.csdnimg.cn/3d5e271bafdd469c98c072727c6188b4.png)