本文主要介绍神经网络中常用的归一化方法，主要是在神经网络内部对中间层的输入进行归一化，归一化到均值为 0 方差为 1 的近似正态分布的模式。

一、为什么神经网络需要归一化

归一化的效果：

• 加速模型的训练和收敛，让模型能更好的学习到输入的分布情况，不受量纲的影响。
• 将数据规范化到激活函数敏感区域，缓解神经网络的梯度消失问题
• 防止过拟合

二、常用的归一化方法

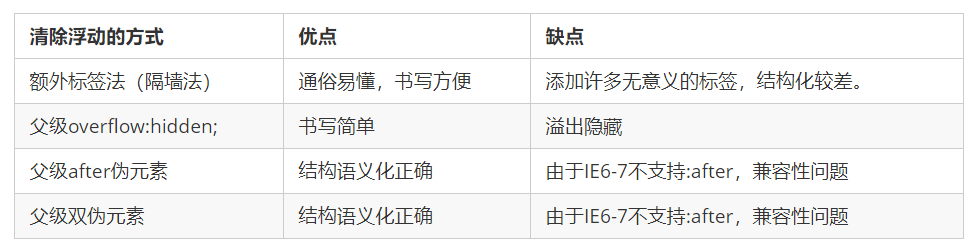
通常情况下，一个 batch 中会包含 N 个图像，每个图像会对应的 C 个通道：

• Batch Norm：是 N 维度的归一化，是指对一个 batch 内，所有图像对应的相同通道进行归一化
• Layer Norm：是 C 维度的归一化，是指对一个 batch 内，一个图像对应的所有通道进行归一化
• Instance Norm：是单个通道维度上的归一化， 是指对一个 batch 内，每个图像的每个通道分别进行归一化
• Group Norm：是分组后的 C 维度上的归一化，是指对一个 batch 内，一个图像对应的所有通道进行分组归一化

三、Batch Normalization

论文：Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift

出版时间： 2015

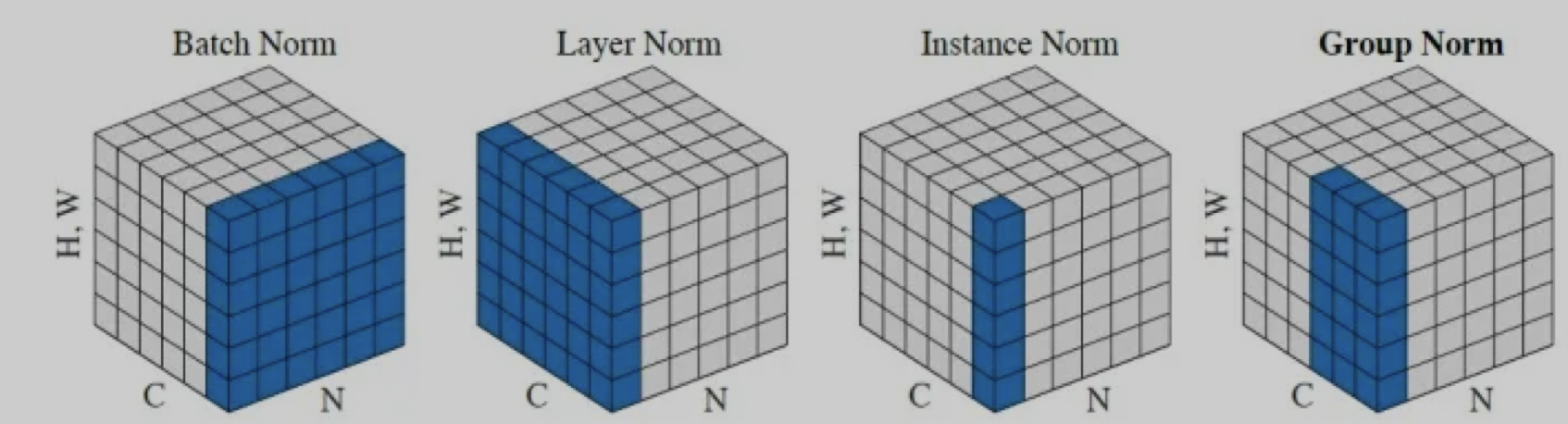
Batch Normalization 是 N 维度的归一化，是指对一个 batch 内，所有图像对应的相同通道进行归一化，过程如下图所示：

BN 的过程：

• 求每一个训练批次数据的均值
• 求每一个训练批次数据的方差
• 使用求得的均值和方差对该批次的训练数据做归一化，获得（0，1）正态分布。其中 ε 是为了避免除数为 0 时所使用的微小正数。
• 网络自主学习尺度变换参数 $\gamma$ 和偏移参数 $\beta$：将 $x_i$ 乘以 $\gamma$ 调整数值大小，再加上 $\beta$ 增加偏移后得到 $y_i$，这里的 $\gamma$ 是尺度因子， $\beta$ 是平移因子。这一步是 BN 的精髓，由于归一化后的 $x_i$基本会被限制在正态分布下，使得网络的表达能力下降。为解决该问题，我们引入两个新的参数： $\gamma$ 和 $\beta$ 。 $\gamma$ 和 $\beta$ 是在训练时网络自己学习得到的，让网络自己去学习更合适的归一化分布。

BN在训练和测试时的差别 :

• 在训练时，是对每一批的训练数据进行归一化。使用 BN 的目的就是每个批次分布稳定。当一个模型训练完成之后，它的所有参数都确定了，包括均值和方差，$\gamma$ 和 $\beta$。

• 在测试时，比如进行一个样本的预测，就并没有 batch 的概念，因此，这个时候用的均值和方差是全量训练数据的均值和方差，也就是使用全局统计量来代替批次统计量，这个可以通过移动平均法求得。具体做法是，训练时每个批次都会得到一组（均值、方差），然后对这些数据求数学期望！每轮batch后都会计算，也称为移动平均。

BN训练时为什么不用整个训练集的均值和方差？

• 因为用整个训练集的均值和方差容易过拟合，对于 BN，其实就是对每一批数据进行归一化到一个相同的分布，而每一批数据的均值和方差会有一定的差别，而不是固定的值，这个差别能够增加模型的鲁棒性，也会在一定程度上减少过拟合。

BN的优点：

• 能够解决内部协变量偏移
• 缓解了梯度饱和问题（如果使用sigmoid函数的话），加快收敛。

BN的缺点：

• batch_size 较小的时候，效果较差，因为 BN 就是用 batch_size 中样本的均值和方差去模拟全部样本的均值和方差，这个假设在样本很少的情况下确实是不合理的
• 不适合 RNN 那种循环网络

四、Layer Normalization

Layer Normalization 是 C 维度的归一化，是指对一个 batch 内，一个图像对应的所有通道进行归一化

公式如下，和 BN 一样，也会在归一化后的分布基础上再学习一个缩放参数 $\gamma$ 和偏移参数 $\beta$：

$$\text{y}=\frac{\text{x}-\text{E(x)}}{\sqrt{\text{Var(x)}+ϵ}}\times \gamma +\beta$$

五、Instance Normalization

Instance Normalization 是单个通道维度上的归一化， 是指对一个 batch 内，每个图像的每个通道分别进行归一化。

公式如下，和 BN 一样，也会在归一化后的分布基础上再学习一个缩放参数 $\gamma$ 和偏移参数 $\beta$：

$$\text{y}=\frac{\text{x}-\text{E(x)}}{\sqrt{\text{Var(x)}+ϵ}}\times \gamma +\beta$$

六、Group Normalization

Group Normalization 是分组后的 C 维度上的归一化，是指对一个 batch 内，一个图像对应的所有通道进行分组归一化。

公式如下，和 BN 一样，也会在归一化后的分布基础上再学习一个缩放参数 $\gamma$ 和偏移参数 $\beta$：

$$\text{y}=\frac{\text{x}-\text{E(x)}}{\sqrt{\text{Var(x)}+ϵ}}\times \gamma +\beta$$