概率基本定义
先验分布：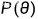
似然函数：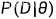
后验分布：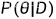
贝叶斯公式：
，其中
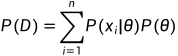
后验分布 = 似然函数 × 先验分布 / P(D)
贝叶斯公式
假设，现在有两个一定概率发生的事件A和B，且它们之间存在一定的关系
P(A) 表示事件A发生的概率
P(B) 表示事件A发生的概率
P(A|B) 表示事件B已经发生的前提下，事件A发生的概率
P(B|A) 表示事件A已经发生的前提下，事件B发生的概率
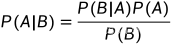
极大似然估计（MLE）
极大似然估计方法（Maximum Likelihood Estimate，MLE）也称为最大概似估计或最大似然估计，是求估计的方法之一
简单来讲，极大似然估计就是给定模型，然后通过收集数据，求该模型的参数。
似然函数形式：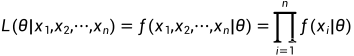 
连乘不好求解，通常会进行一个对数变换，转换为累加：
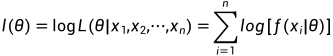
伯努利分布
每一个样本的概率可以表示为：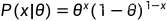
,x=0 or 1,
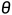是成功的概率
假设有n个样本，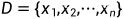
对数最大似然函数表达式：
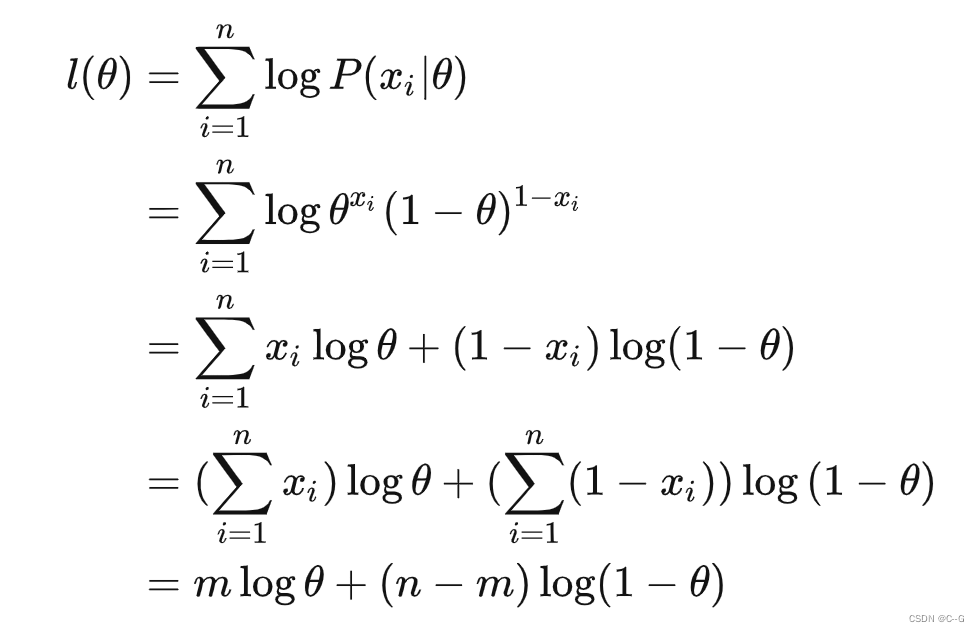
对上式求导，解得当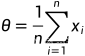
，似然函数取得最大值
正态分布
样本概率表示为：
假设有n个样本，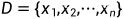
对数最大似然函数表达式：
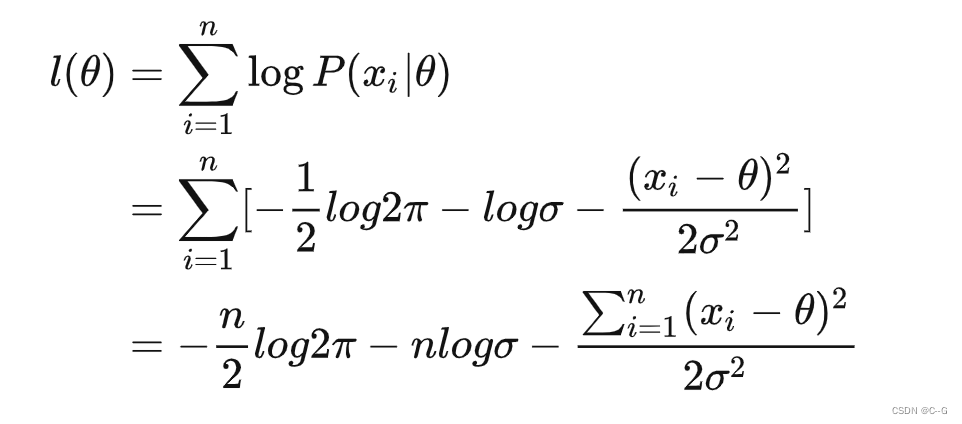
对上式求导，解得当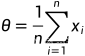，似然函数取得最大值
例子
路人甲在一个不透明的袋里放了若干个黑色和白色的球；路人乙想知道袋中球的情况，就从袋中有放回式取球，一共取了10次，有7次是白球，3次是黑球。问白球的比例是多少？
在这个例子中，每一次实验都是服从伯努利分布，我们设白球的概率为,样本为
，似然函数为：
,取对数，求最大值为
最大后验估计（MAP）
Maximum A Posteriori Estimation
在最大似然估计的例子中，如果样本数量不够多，其实存在着很大的问题
MLE简单又客观，但是过分的客观有时会导致过拟合(Over fitting)。在样本点很少的情况下，MLE的效果并不好
一个最简单的例子就是，一个伯努利模型，我们知道通过最大似然估计得到的先验值为
最大似然估计认为使似然函数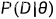 
最大的参数 θ 即为最好的 θ ；
最大后验估计认为使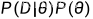 
最大的参数 θ 即为最好的 θ ；
最大似然估计可以看作是一种特殊的最大后验估计，将 θ 看作是固定的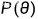， =1 。
最大后验概率估计的公式表示：（P(D)是一个常数，与 θ 无关）
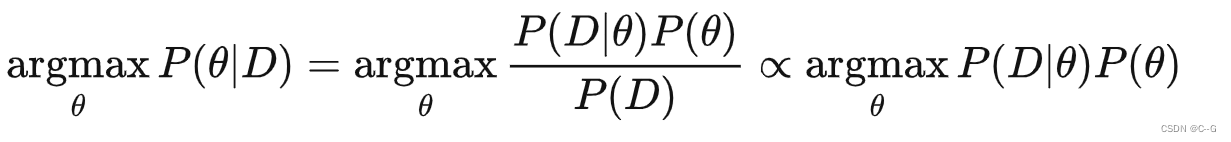
要求解MAP，还需要知道参数的先验分布
正态分布
假设高斯分布方差已知，现在要估计均值，将均值记为 θ
每一个样本的概率可以表示为 
假设 θ 服从高斯分布,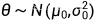
,则
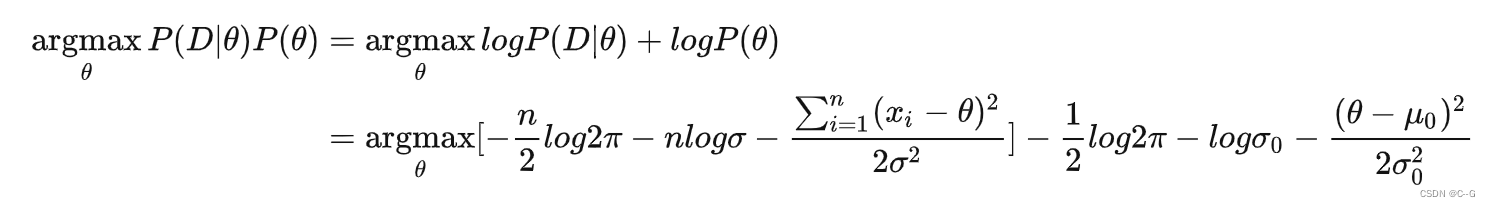
求解得到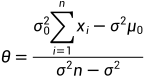 
例子
路人甲在一个不透明的袋里放了若干个黑色和白色的球，他感觉白色球更多；路人乙想知道袋中球的情况，就从袋中有放回式取球，一共取了10次，有7次是白球，3次是黑球。问白球的比例是多少？
每一次实验都是服从伯努利分布，我们设白球的概率为 θ ，所以每一次实验可以表示为：
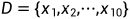
路人甲的感觉是白色球更多，需要给出一个 θ 的分布，假设 P(θ) = 2θ
后验概率函数：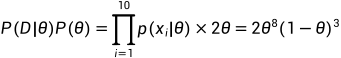
取对数，求最大值 θ = 0.73
当样本个数无穷多的时候，MAP上会逼近MLE，因为样本足够多了，就不需要先验了，或者比起先验更相信样本。
贝叶斯估计
最大似然估计和最大后验估计都是估计了参数的具体值，但更令人信服的其实是参数的分布，知道参数在取每个值时的概率。
与最大后验估计一样，需要用到贝叶斯定理
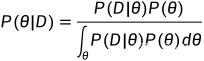
需要知道先验分布 P(θ),但此时不再求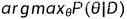 
,而要求出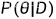
这里如果先验分布十分复杂，上式会很难求解（因为要分母积分），所以一般会选择共轭先验。
二项分布参数的共轭先验是Beta分布，多项式分布参数的共轭先验是Dirichlet分布，指数分布参数的共轭先验是Gamma分布，⾼斯分布均值的共轭先验是另⼀个⾼斯分布，泊松分布的共轭先验是Gamma分布。
最大后验估计和贝叶斯估计也存在一个问题，实际应用场景中的先验概率不是那么好求，很多都是拍脑袋决定的。一旦是拍脑袋决定的，自然也就不准了，先验概率不准，那么计算出的后验概率也就相应的不准了
贝叶斯估计用来预测新测量数据的概率，对于新出现的数据 x
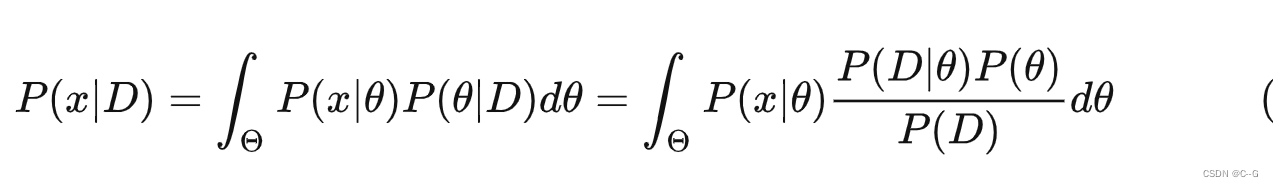
例子
路人甲在一个不透明的袋里放了若干个黑色和白色的球，他感觉白色球更多；路人乙想知道袋中球的情况，就从袋中有放回式取球，一共取了10次，有7次是白球，3次是黑球。问白球的比例是多少？
每一次实验都是服从伯努利分布，我们设白球的概率为 θ ，所以每一次实验可以表示为：
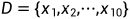
路人甲的感觉是白色球更多，需要给出一个 θ 的分布，假设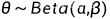
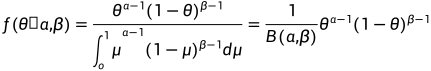
后验概率函数
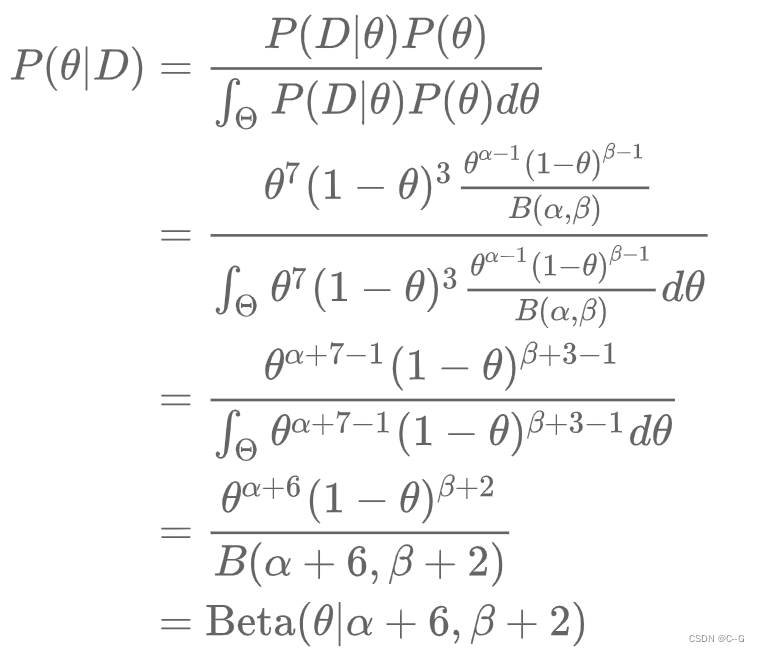
得到了参数的后验分布情况，得到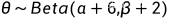
计算步骤
根据贝叶斯定理，计算后验概率P(θ|D)
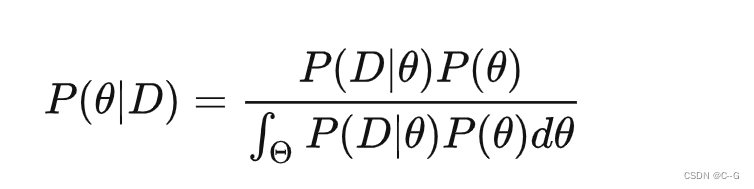
计算新样本估计
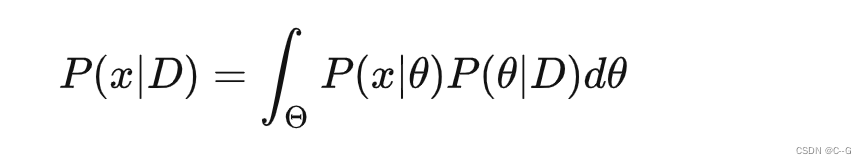
总结
MLE、MAP是选择相对最好的一个模型， 贝叶斯方法则是通过观测数据来估计后验分布，并通过后验分布做群体决策，所以后者的目标并不是在去选择某一个最好的模型，而是去评估每一个模型的好坏。
参考于：一文解释 参数估计 - 知乎 (zhihu.com)
