2019年第九届MathorCup高校数学建模挑战赛
A题 数据驱动的城市轨道交通网络优化策略
原题再现:
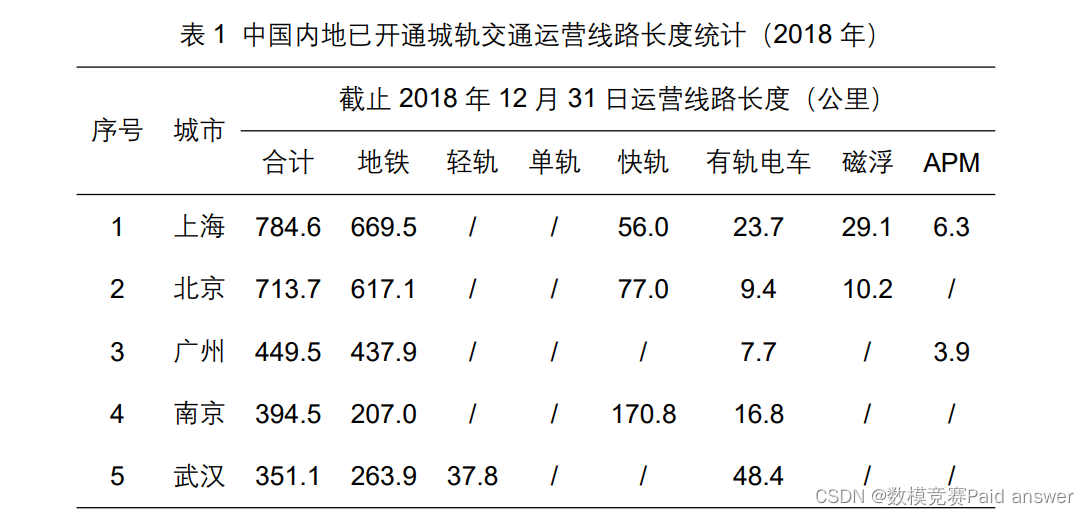
截至 2018 年 12 月 31 日,中国内地累计共有 35 座城市建成并投运城市轨道交通,里程共计 5766.6 公里。进入“十三五”以来,三年累计新增运营线路长度为 2148.7公里,年均新增线路长度为 716.2 公里(2018 中国城市轨道交通协会快报)。表 1 统计了 2018 年中国内地城轨交通运营线路长度排名前 5 的各大城市。以北京市为例,其轨道交通覆盖 11 个市辖区,运营里程约 714 公里,共设车站 391 座,开通里程居中国第二位。此外,据 2017 年统计,北京城市轨道交通年乘客量全年达到 45.3 亿人次,日均客流为 1241.1 万人次,单日客运量最高达 1327.46 万人次。可见,城市轨道交通已成为大城市居民出行的主要载体,也是城市发展的重要支撑。
目前,北上广等城市轨道交通客流量大,乘客出行的 O-D 数据缤繁复杂,以北京城市轨道交通网络为例,现需要你对给定的历史数据进行以下分析和评估:
问题 1:附件 1 给出了北京市某时段部分城市轨道交通线网的乘客 O-D 数据,附件2 为基础信息数据,附件 3 为该时段的列车运行图数据。依据北京城市轨道交通线网图(附件 4),试分析基于以上数据的乘客出行特征,包括出行时段分布、出行距离分布、
出行时长分布等。
问题 2:基于问题 1 的路径选择结果,设计一套算法还原乘客出行的准确信息,即乘客在何时何站搭乘何辆地铁列车(如有换乘,需计算)并在何时何地出站,完成其一次完整的地铁出行,并完整填写表 2(计算乘客编号为 2、7、19、31、41、71、83、89、101、113、2845、124801、140610、164834、193196、223919、275403、286898、314976、315621 的完整出行线路)。另外,设计一套智能算法,以辅助并优化乘客的在轨道交通路网中的路径选择,如通过优化路径可缩短行程、减少拥挤等。

问题 3:假设地铁八通线每列列车容量为 1428 人,列车座位数为 256 座,限流时段长度可根据需要任选,且以 7:00 为首班列车发车时刻,在减小列车超载现象的基础上,尽可能缩短乘客出行时间(包括出行时间和滞留时间),并以此为目标建立城市轨道交通单一线路乘客限流模型。对模型求解后给出具体限流措施以改进八通线的服务水平,具体包括:
问题 3.1:若八通线不限制限流车站个数,试分析限流前后的总出行时间、平均出行时间对比,结果如表 3 所示。
问题 3.2:若八通线限制限流车站个数(分别取限流车站数为 1-5 个车站),试分析限流前后的总出行时间、平均出行时间对比,结果如表 4 所示。
问题 3.3:根据以上分析结果,举例说明八通线两个限流效果最好的车站,并阐述原因。


问题 4:结合问题 1-3,给出具体限流措施以改进城市轨道交通的服务水平,如动态限流方案、限流车站的选取、限流时段的选择、限流强度等。
整体求解过程概述(摘要)
随着我国城市轨道交通建设的快速发展,轨道交通信息化水平的不断提高,轨道交通各系统获取的数据量飞速增长且规模日渐庞大,如何基于海量数据进行分析并发挥这些海量数据价值逐渐成为研究特点。本文主要研究数据驱动下的城市轨道交通网络优化策略,研究北京市乘客出行特征,还原乘客准确出行信息以及乘客最优路径选择,并制定乘客限流方案和限流措施,进而提高城市轨道交通线路规划、运输组织协调,改进城市轨道交通的服务水平。
问题一中:根据北京市某时段部分城市轨道交通线网数据,首先采用SPSS软件对数据进行统计分析,并对异常数据进行处理,其次对乘客出行特征(客流时间分布、客流空间分布和客流时空分布)进行分析,从出行时段分布、出行时长分布,线路客流分布、车站客流的分布、车站客流乘降差分布,不同时间段各线路的进出站客流分布不同角度研究,并从中得出一系列结论,为北京市城市轨道交通规划、运输组织、限流方案等提供参考依据。
问题二中:首先基于图论的相关知识建立相邻车站走向时间的带权邻接矩阵用于还原乘客出行信息以及乘客最优路径选择,在乘客出行信息还原模型中,建立含有限制条件的 KSP 模型及算法,并以乘客#2 为例详细介绍路径还原过程,得到乘客#2 的完整出行路径为:西红门→宣武门→北京站(4 号线→2 号线),列车编号为 419093→213001。 在乘客最优路径选择中,引入路径阻抗,路径伸展系数建立改进的 Dijkstra 模型及算法,为验证该模型的准确性和合理性,验证天安门西站→关庄站的最优路径选择,求解结果与北京地铁官方网站路线方案查询结果完全吻合,最优时间计算为 43.26min,与查询时间基本一致;最后,考虑该时刻5号线的拥挤情况,此时最优方案共耗时46.92min,小于考虑拥挤时原先方案所耗时的 52.03min,进一步验证该模型的的科学性和运算的准确性。
问题三中:在分析大客流条件下乘客候车延误影响因素的基础上,考虑列车周期性运行特性,并抽象乘客到达规律符合均匀分布,以各站乘客均衡候车为优化目标,构建线路层车站间的单目标多约束协同限流模型,在不限制限流车站个数下,基于 Matlab 非线性规划 fmincon 函数进行模型求解,在限制限流车站个数下,采用基于改进模拟退火算法进行模型求解结果表明,选择双桥、管庄进行限流,双桥的减少率最高,双桥、管庄进行限流时累计减少率达到 17.3%。通过与北京八通线已有的限流车站以及从计算结果的趋势性对比体现了模型的有效性和合理性。
问题四中:基于问题一客流乘客出行特征(客流时间分布、客流空间分布和客流时空分布)的分析数据以及问题三限流模型和限流方案,提出采用动态限流方案、限流车站的选取、限流时段的选择、限流强度等多种措施对城市轨道交通多站协同客流控制问题进行研究的方法。基于对北京市城市轨道交通客流限流控制策略研究,有效解决目前研究的限流方案难以根据动态客流变化做出相应的调整的问题,进一步丰富城市轨道交通客流需求管理的理论和方法。
模型假设:
问题一假设:
(1)列车按计划时刻表运行,无晚点或其他突发事件发生;
(2)假设进站客流为同一控制时间段内均匀到达,状态稳定;
(3)假设线网乘客 O-D 数据、线网基础信息表、列车运行图数据真实有效;
(4)在总限流时段内,车站进站口及站台的客流,都符合均匀到达规律,视为均匀分布;
(5)已知高峰时段客流需求量及起讫点(下称 OD 点),考虑到高峰时段客流组成多为通勤客流,其结构稳定,可通过历史数据分析获得较高精度的 OD 客流信息。
问题二假设:
(1)乘客可正常上车,不受下车客流的逆向影响,不故意绕路,故意不下车;
(2)进站口到达乘客仅有被限流和进入站台两种状态,不存在放弃出行需求的行为;
(3)列车发车间隔时间固定,且严格按照计划时刻表运行,在实际运营中,在不发生故障的情况下,城市轨道交通列车准点率极高,可假定为按照计划时刻表运行。
问题三假设:
(1)乘客不存在主观留乘行为,当列车能力未达饱和,乘客可继续上车时,站台乘客不会选择等候下一趟列车;
(2)仅研究单向的列车运行过程,由于城市轨道交通常态化限流时段的客流潮汐特征明显,因此本文仅研究单一方向上的协同限流策略,模型输入参数如未进行特殊说明,均为处理后的单方向输入参数;
(3)进站乘客进入站台后,仅可通过上车接受运输服务离开其出发车站,不会再次返回其出发车站进站口离站;
(4)客流需求总量保持不变,即计算客流不考虑转移到其他交通方式;
(5)简化乘客在车站付费区的走行过程。不考虑进出站通道对乘客的影响,模型主要从线路层面考虑协同限流策略,因此忽略站内基础设施的影响,即经过进站口的乘客,在限流过后,可直接到达车站站台,简化乘客站内走行时间;
(6)在实际运营中,出站客流能快速离开车站,模型忽略其对站台及进站口客流的影响。
问题分析:
问题 1 的分析
城市轨道交通运营客流是动态变化的,对客流调查数据进行统计分析,可以了解客流在时间、空间上的动态变化规律;同时对既有线路的运营客流特征分析,也能为后续实施线路或者其他城市的规划路网提供参考数据,从而为其线网规模的控制、基建工程和设备采用与布置以及运输组织等诸多方面提供参考。在进行乘客出行特征分析之前,需对海量数据进行统计收集,深入研究分析的各数据间的关系和含义,并对异常数据进行处理。根据轨道交通路网层次将客流特征分为车站客流特征、线路客流特征和网络客流特征三类,将北京市城市轨道交通乘客出行分别按照时间、空间、时空进行分析。
问题 2 的分析
问题 2 主要包括两个问题:第一:还原乘客一次出行的准确信息,即乘客在何时何站搭乘何辆地铁列车(如有换乘,需计算)并在何时何地出站,由于乘客进站位置,出站位置以及进站时间和和出站时间是确定的,路径还原即为在限制条件下的多解问题。第二:建立智能算法辅助并优化乘客在轨道交通路网中的路径选择,即为选择耗时时间最短路径下的最优解问题,通过选择最优路径缩短行程、提高乘客换乘效率、优化站内客流并减少拥挤。
问题 3 的分析
由于本文主要研究单线协同限流策略,重点分析线路上各车站限流人数与限流时间的关系,因此,本文的决策变量为车站限流人数,车站进站口聚集人数中,因受到限流影响而未能进入车站站台的人数。城市轨道交通运营方迫于站台能力和列车能力的限制,当线路客流量较大时,分别在各站进站口采取一定措施,限制部分乘客的进站,从而对站内候车人数进行一定规模的控制,使整条线路的运营达到最优状态。基于以上分析,所建模型的目标函数为最小化乘客总出行延误时间乘客总出行延误时间应为在总限流时段内全线各站乘客出行延误时间的总和,为一维数值形式。因此,可通过数学方法,制定使全线乘客总出行延误时间最小化的单线协同限流策略。
问题 4 的分析
问题 4 要求给出具体限流措施以改进城市轨道交通的服务水平,针对城市轨道交通系统具有的动态时变特点,提出了采用动态时域优化对城市轨道交通多站协同客流控制问题进行研究的方法。基于动态时域的客流控制策略,实现对限流方案的持续优化,有效解决了目前研究的限流方案难以根据动态客流变化做出相应的调整的问题。这种通过持续动态地对既有的限流方案进行动态评价、及时调整和优化思想,考虑了城市轨道交通系统的客流动态性和全局性,实现了客流不均衡条件的动态削峰及路网能力高效利用。同时,也进一步丰富了城市轨道交通客流需求管理的理论和方法。
模型的建立与求解整体论文缩略图



全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
程序代码:(代码和文档not free)
The actual procedure is shown in the screenshot
function [] = all_paths_gen(weight_matrix, k, output_file)
len = length(weight_matrix);
fileID = fopen(output_file,'wt');
fprintf(fileID,'%d nodes \n\n', len);
fclose(fileID);
node_pairs = combnk(1:len,2);
for index = 1: length(node_pairs)
src = node_pairs(index, 1);
dst = node_pairs(index, 2);
gen_k_shortest_path(weight_matrix, src, dst, k, output_file, index);
end
function [shortestPath, totalCost] = dijkstra(netCostMatrix, s, d)
n = size(netCostMatrix,1);
for i = 1:n
% initialize the farthest node to be itself;
farthestPrevHop(i) = i; % used to compute the RTS/CTS range;
farthestNextHop(i) = i;
end
% all the nodes are un-visited;
visited(1:n) = false;
distance(1:n) = inf; % it stores the shortest distance between each node and the source node;
parent(1:n) = 0;
distance(s) = 0;
for i = 1:(n-1),
temp = [];
for h = 1:n,
if ~visited(h) % in the tree;
temp=[temp distance(h)];
else
temp=[temp inf];
end
end;
[t, u] = min(temp); % it starts from node with the shortest distance to the source;
visited(u) = true; % mark it as visited;
for v = 1:n, % for each neighbors of node u;
if ( ( netCostMatrix(u, v) + distance(u)) < distance(v) )
distance(v) = distance(u) + netCostMatrix(u, v); % update the shortest distance when a
shorter shortestPath is found;
parent(v) = u; % update its parent;
end;
end;
end;
shortestPath = [];
if parent(d) ~= 0 % if there is a shortestPath!
t = d;
shortestPath = [d];
while t ~= s
function [shortestPaths, totalCosts] = gen_k_shortest_path(weight_matrix, src, dst, k, output_file,
demand_id)
fileID = fopen(output_file,'at');
%------Call kShortestPath------:
[shortestPaths, totalCosts] = kShortestPath(weight_matrix, src, dst, k);
%------Display results------:
if isempty(shortestPaths)
fprintf(fileID,'No path available between these nodes\n\n');
else
for i = 1: length(shortestPaths)
%fprintf(fileID,'Path # %d: %d %d : ',i, src, dst);
fprintf(fileID,'%d %d ', src, dst);
%disp(shortestPaths{i});
len = length(shortestPaths{i});
for j = 1: len - 1
fprintf(fileID, '%d ', shortestPaths{i}(j));
end
fprintf(fileID,'%d', shortestPaths{i}(len));
%fprintf(fileID,'x_%d_%d \n', demand_id, i);
fprintf(fileID,'\n');
%fprintf(fileID,'Cost of path %d is %5.2f\n\n',i,totalCosts(i));
end
end
fclose(fileID);
function [shortestPaths, totalCosts] = kShortestPath(netCostMatrix, source, destination,
k_paths)
if source > size(netCostMatrix,1)
destination > size(netCostMatrix,1)
warning('The source or destination node are not part of netCostMatrix');
shortestPaths=[];
totalCosts=[];
else
k=1;
[path cost] = dijkstra(netCostMatrix, source, destination);
%P is a cell array that holds all the paths found so far:
if isempty(path)
shortestPaths=[];
totalCosts=[];
else
path_number = 1;
P{path_number,1} = path; P{path_number,2} = cost;
current_P = path_number;
%X is a cell array of a subset of P (used by Yen's algorithm below):
size_X=1;
X{size_X} = {path_number; path; cost};
%S path_number x 1
S(path_number) = path(1); viation vertex is the first node initially
% K = 1 is the shortest path returned by dijkstra():
shortestPaths{k} = path ;
totalCosts(k) = cost;
while (k < k_paths && size_X ~= 0 )
%remove P from X
for i=1:length(X)
if X{i}{1} == current_P
size_X = size_X - 1;
X(i) = [];lete cell
break;
end
end
P_ = P{current_P,1}; %P_ is current P, just to make is easier for the notations
%Find w in (P_,w) in set S, w was the dev vertex used to found P_
w = S(current_P);
for i = 1: length(P_)
if w == P_(i)
w_index_in_path = i;
end
end
for index_dev_vertex= w_index_in_path: length(P_) - 1 %index_dev_vertex is
index in P_ of deviation vertex
temp_netCostMatrix = netCostMatrix;
%------
%Remove vertices in P before index_dev_vertex and there incident edges
for i = 1: index_dev_vertex-1
v = P_(i);
temp_netCostMatrix(v,:)=inf;
temp_netCostMatrix(:,v)=inf;
end
%------
%remove incident edge of v if v is in shortestPaths (K) U P_ with similar
sub_path to P_....
SP_sameSubPath=[];
index =1;
SP_sameSubPath{index}=P_;
for i = 1: length(shortestPaths)
if length(shortestPaths{i}) >= index_dev_vertex
if P_(1:index_dev_vertex) == shortestPaths{i}(1:index_dev_vertex)
index = index+1;
SP_sameSubPath{index}=shortestPaths{i};
end
end
end
v_ = P_(index_dev_vertex);
for j = 1: length(SP_sameSubPath)
next = SP_sameSubPath{j}(index_dev_vertex+1);
temp_netCostMatrix(v_,next)=inf;
end
%------
%get the cost of the sub path before deviation vertex v
sub_P = P_(1:index_dev_vertex);
cost_sub_P=0;
for i = 1: length(sub_P)-1
cost_sub_P = cost_sub_P + netCostMatrix(sub_P(i),sub_P(i+1));
end
[dev_p c] = dijkstra(temp_netCostMatrix, P_(index_dev_vertex),
destination);
if ~isempty(dev_p)
path_number = path_number + 1;
P{path_number,1} = [sub_P(1:end-1) dev_p] ; %concatenate sub path- to
-vertex -to- destination
P{path_number,2} = cost_sub_P + c ;
S(path_number) = P_(index_dev_vertex);
size_X = size_X + 1;
X{size_X} = {path_number; P{path_number,1} ;P{path_number,2} };
else
%warning('k=%d, isempty(p)==true!\n',k);
end
end
%Step necessary otherwise if k is bigger than number of possible paths
%the last results will get repeated !
if size_X > 0
shortestXCost= X{1}{3}; %cost of path
shortestX= X{1}{1}; %ref number of path
for i = 2 : size_X
if X{i}{3} < shortestXCost
shortestX= X{i}{1};
shortestXCost= X{i}{3};
end
end
current_P = shortestX;
%******
k = k+1;
shortestPaths{k} = P{current_P,1};
totalCosts(k) = P{current_P,2};
%******
else
%k = k+1;
end
end
end
end