目录
一、前言
二、Dijkstra算法
1、Dijkstra 算法简介
2、算法思想:多米诺骨牌
3、算法实现
4、例子
三、例题
1、蓝桥王国(lanqiaoOJ题号1122)
一、前言
本文主要讲了Dijkstra算法的概念、实现与一道模板例题。
二、Dijkstra算法
1、Dijkstra 算法简介
- Dijkstra:单源最短路径问题。
- 优点:非常高效而且稳定。
- 缺点:图的边权不能为负值。
- 思路:贪心思想+优先队列+BFS。
2、算法思想:多米诺骨牌
- 在图中所有的边上,排满多米诺骨牌。
- 一条边上的多米诺骨牌数量,等于边的权值。
- 规定所有骨牌倒下的速度都一样。在一个结点上推倒骨牌,会导致这个结点上的所有骨牌都往后面倒下去。
- 在起点 s 推倒骨牌,从 s 开始,它连接的边上的骨牌都逐渐倒下,并到达所有能达到的结点。
- 在某个结点 t,可能先后从不同的线路倒骨牌过来。
- 先倒过来的骨牌,其经过的路径,肯定就是从 s 到达 t 的最短路;
- 后倒过来的骨牌,对确定结点 t 的最短路没有贡献,不管它。
- 在 s 的所有直连邻居中,最近的邻居 u,骨牌首先到达。u 是第一个确定最短路径的结点。从u 直连到 s 的路径肯定是最短的,因为如果 u 绕道别的结点到 s,必然更远。
- 然后,把后面骨牌的倒下分成 2 部分,一部分是从 s 继续倒下到 s 的其它的直连邻居,另一部分从 u 出发倒下到 u 的直连邻居。下一个到达的结点 v,必然是 s 或者 u 的一个直连邻居。v 是第二个确定最短路径的结点。
- 继续以上步骤,在每一次迭代过程中,都能确定一个结点的最短路径。
【特点】
- Dijkstra 算法应用了贪心法的思想,即 “抄近路走,肯定能找到最短路径”。
- 算法高效稳定:
- >Dijkstra的每次迭代,只需要检查上次己经确定最短路径的那些结点的邻居,检查范围很小,算法是高效的;
- >每次迭代,都能得到至少一个结点的最短路径,算法是稳定的。
3、算法实现
【维护两个集合】
己确定最短路径的结点集合 A、这些结点向外扩散的邻居结点集合B。
1)把起点 s 放到 A 中,把 s 所有的邻居放到 B 中。此时,邻居到 s 的距离就是直连距离。
2)从 B 中找出距离起点 s 最短的结点 u,放到 A 中。3)把 u 所有的新邻居放到 B 中。显然,u 的每一条边都连接了一个邻居,每个新邻居都要加进去。其中 u 的一个新邻居 v,更新它到 s 的距离 dis(s,w),等于 dis(s,w) 和 dis(s,u)+dis(u,w) 的最小值。
4)重复(2)、(3),直到 B 为空时,结束。
【优先队列】
- 每次往 B 中放新数据时,按从小到大的顺序放,用二分法的思路,复杂度是 O(logn),保证最小的数总在最前面:
- 找最小值,直接取 B 的第一个数,复杂度是 O(1)。
- 复杂度:用优先队列时,Dijkstra 算法的复杂度是 O(mlogn),是最高效的最短路算法。
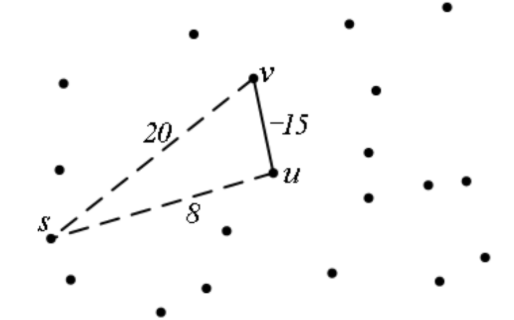
【边权不能为负】
- Dijkstra 的局限性是边的权值不能为负数
- Dijkstra 基于 BFS,计算过程是从起点 s 逐步往外扩散的过程,每扩散一次就用贪心得到到一个点的最短路。
- 扩散要求路径越来越长,如果遇到一个负权边,会导致路径变短,使扩散失效。
- 设当前得到 s->u 的最短路,路径长度为 8,此时 s->u 的路径计算己经结束。
- 继续扩展 u 的邻居,若 u 到邻居 v 的边权是 -15,而 v 到 s 的距离为 20,那么 u 存在另一条途径 v 到 s 的路径,距离为 20+(-15)=5,这推翻了前面己经得到的长度 8 的最短路,破坏了 BFS 的扩散过程。
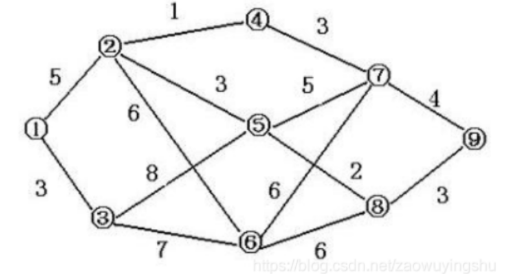
4、例子
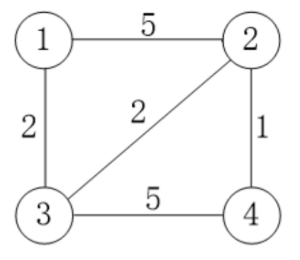
起点是 1,求 1 到其它所有结点的最短路径。
1)1 到自己的距离最短,把 1 放到集合A里:A=11。把 1 的邻居放到集合 B 里:B={ (2-5),(3-2)}。其中(2-5)表示结点 2 到起点的距离是 5。
2)从 B 中找到离集合 A 最近的结点,是结点 3。在 A 中加上 3,现在 A={1,31},也就是说得到了从 1 到 3 的最短距离;从 B 中拿走 (3-2),现在 B={(2-5)}
3)对结点 3 的每条边,扩展它的新邻居,放到 B 中。3 的新邻居是 2 和 4,那么 B={(2-5),(2-4),(4,7)}。其中 (2-4) 是指新邻居 2 通过 3 到起点 1,距离是 4。由于 (2-4) 比 (2-5) 更好,丢弃 (2-5),B={ (2-4),(4-7) }。
4)重复步骤(2)、(3)。从 B 中找到离起点最近的结点,是结点 2。在 A 中加上 2,并从 B 中拿走 (2-4);扩展 2 的邻居放到 B 中。现在 A={1,3,2},B={(4-7),(4-5)}。由于 (4-5) 比 (4-7) 更好,丟弃 (4-7),B={(4-5)}。
5)从 B 中找到离起点最近的结点,是结点 4。在 A 中加上 4, 并从 B 中拿走 (4-5)。已经没有新邻居可以扩展。现在 A=(1,3,2,4},B 为空,结束。
三、例题
1、蓝桥王国(lanqiaoOJ题号1122)
【题目描述】
蓝桥王国一共有 N 个建筑和 M 条单向道路,每条道路都连按着两个建筑,每个建筑都有自己编号,分别为 1~N。(其中皇宫的编号为1)
国王想让小明回答从 皇宫到每个建筑的最短路径是多少,但紧张的小明此时己经无法思考,请你编写程序帮助小明回答国王的考核。
【输入描达】
输入第一行包含 2 个正整数 N,M。第 2 到 M+1 行每行包含三个正整数 u,v,w, 表示 u->v 之问存在一条距离为 w 的路。1≤N≤3×10^5,1≤m≤10^6,1<=ui, vi<=N,0≤wi≤10^9。
【输出描述】
输出仅一行,共 N 个数,分别表示从皇宫到编号为 1~N 建筑的最短距离,两两之问用空格隔开。(如果无法到达则输出 -1)
【输入】
3 3
1 2 1
1 3 5
2 3 2
【输出】
0 1 3
【我的题解】(已AC)
import heapq
def dij(s):
A=[0]*(n+1) #已找到最短路径顶点的集合
B=[]
dis[s]=0
heapq.heappush(B,(0,s))
while B:
u=heapq.heappop(B)[1]
if A[u]:
continue
A[u]=1 #加入A集合
for v,w in mp[u]:
if A[v]:
continue
if dis[v]>dis[u]+w:
dis[v]=dis[u]+w
heapq.heappush(B,(dis[v],v))
n,m=map(int,input().split())
mp=[[] for _ in range(n+1)] #邻接表存图
INF=1<<64
dis=[INF]*(n+1) #1到每个点的距离全部初始化为无穷大
for _ in range(m):
u,v,w=map(int,input().split())
mp[u].append((v,w))
s=1
dij(s)
for i in range(1,n+1):
if dis[i]>=INF:
print(-1,end=" ")
else:
print(dis[i],end=" ")
#这样输出竟然也正确
#for i in range(1,n+1):
# if i==n:
# if dis[i]>=INF:
# print(-1)
# else:
# print(dis[i])
# else:
# if dis[i]>=INF:
# print(-1,end=" ")
# else:
# print(dis[i],end=" ")以上, Dijkstra算法的入门与应用
祝好