图的存储结构

1.邻接矩阵表示法

设图G = (V, E)是具有n个顶点的图，顶点顺序依次为{v1,v2,v3.......}

设a[N][N]为 n 阶方阵

• G 的邻接矩阵具有此种性质：

  • 若a[i][j]=1，则存在边(vi, vj)或者弧<vi, vj> (即两点之间存在边或弧)
  • 若a[i][j]=0，则不存在边(vi, vj)或者弧<vi, vj> (即两点之间不存在边或弧)

• 特点

  • 无向图的邻接矩阵对称，可压缩存储；有 n 个顶点的无向图所需存储空间为 n(n-1)/2。
  • **有向图的邻接矩阵不一定对称；**有 n 个顶点的有向图所需存储空间为 n²
  • 无向图中顶点 vi 的度是邻接矩阵中第 i 行 1 的个数
  • 有向图中
    • 顶点 vi 的出度是邻接矩阵中第 i 行 1 的个数（向外连弧，即作为弧尾）
    • 顶点 vi 的入度是邻接矩阵中第 i 列 1 的个数（被连入的弧，即作为弧头）

• 存图结构

  • 我们需要定义两个数组
    • 一个一维数组：用来记录顶点的信息
    • 一个二维数组：用来记录顶点之间的关系（同a[i] [j]的描述）

• 示例

  

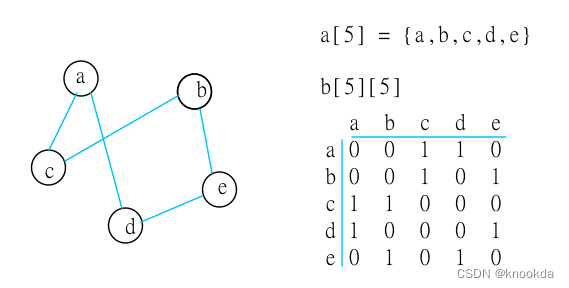
• 存储结构

  #define INFINITY    INT_MAX // 最大值∞ 
  #define MAX_VERTEX_NUM   20 // 最大顶点个数 
  typedef enum {DG, DN, UDG, UDN} GraphKind;  
  							//图的类型{有向图,有向网,无向图,无向网} 
  typedef struct ArcCell 
  { 
     EType adj;  	  // EType是顶点关系类型，对无权图用1或0表示相邻否；                           			     // 对带权图，则为权值类型
     InfoType *info;// 该弧相关信息的指针
  } ArcCell, AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM]; 
  
  typedef struct 
  { 
      VertexType vexs[MAX_VERTEX_NUM]; // 顶点向量(一维矩阵)
      AdjMatrix arcs; 				// 邻接矩阵(二维矩阵)   
      int vexnum, arcnum; 			// 图的当前顶点数和弧(边)数
      GraphKind kind; 				// 图的种类标志
  } MGraph; 
  

2.邻接表表示法

• 存图结构

  • 将所有顶点存入一个表中，作为头结点的表

  • 将与每个头结点有邻接关系的点作为表结点链到头结点之后

    • 头结点包含数据域与指针域
    • 表结点包含邻接点域（邻接点在表头中的位置）与链域（指示下一条边或弧）

    

• 邻接表的特点

  • 顶点 vi 的出度为第 i 个单链表中的结点个数
  • 顶点 vi 的入度为整个单链表中邻接点域值是i-1的结点个数
  • 找出度易，找入度难

• 示例
  

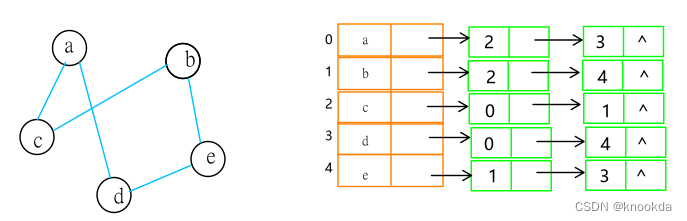
• 存储结构

  #define MAX_VERTEX_NUM 20
  
  //表结点的结构（链表结构）
  typedef struct ArcNode 
  { 
      int adjvex; // 该弧所指向的顶点的位置    
      struct ArcNode *nextarc; // 指向下一条弧的指针  
      //InfoType *info; // 该弧相关信息的指针
  } ArcNode;
  
  //头结点数组
  typedef struct VNode 
  { 
      VertexType data; // 顶点信息
      ArcNode *firstarc; // 指向第一条依附该顶点的弧  
  } VNode, AdjList[MAX_VERTEX_NUM]; 
  
  //组合成的图的结构
  typedef struct 
  { 
      AdjList   vertices; 
      int   vexnum, arcnum; // 图的当前顶点数和弧数  
      int   kind; // 图的种类标志
  } ALGraph; 
  

3.十字链表表示法

• 存图结构

  • 同样由两部分组成：顶点结点和弧结点

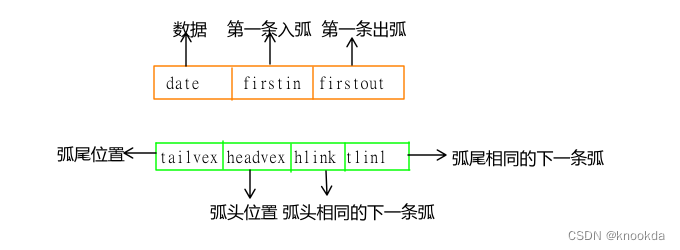
• 存储结构

  #define MAX_VERTEX_NUM 20
  
  typedef struct ArcBox 
  { 
      int tailvex, headvex; 		   // 该弧的尾和头顶点的位置 
      struct ArcBox *hlink, *tlink;  // 分别指向下一个弧头相同和弧尾相同的弧的指针域 
      InfoType *info;   			   // 该弧相关信息的指针 
  } ArcBox;
  
  typedef struct VexNode 
  { 
     VertexType data; 
     ArcBox *firstin, *firstout; // 分别指向该顶点第一条入弧和出弧 
  } VexNode; 
  
  typedef struct 
  { 
     VexNode xlist[MAX_VERTEX_NUM]; // 表头向量 
     int vexnum, arcnum; 			  // 有向图的当前顶点数和弧数 
  } OLGraph;