系列文章目录
提示:这里可以添加系列文章的所有文章的目录,目录需要自己手动添加
TODO:写完再整理
文章目录
- 系列文章目录
- 前言
- 一、路径曲线插值、拟合和逼近的区别
- 1、拟合
- 2、插值
- 3、逼近
- 二、路径点线性插值方法
- (1)纯跟踪(pure_persuit)算法内置的插值算法
- 1.源代码(补充注释了~)
- 2.插值原理解释
- 3.算法优点
- 4.算法缺点
- (2)纯跟踪(pure_persuit)的虚拟点补偿插值算法
- 1.示例图
- 2.代码实现
- (3)普通的线性插值算法
- 1.源代码(补充注释了~)
- 2.源代码解释
- 3.算法优点
- 4.算法缺点
- (4)y0和yf之间的线性插值(x在0和1之间)
- 总结
- 参考资料
- 三、常用的路径抽稀算法
- 抽稀的定义
- 抽稀因子的核心思想
- 一、方法一:步长距离法--步长原则
- 1.算法原理
- 2.算法实现
- 3.算法优点
- 4.算法不足
- 二、方法二:线段过滤法--线段长度原则
- 1.算法原理
- 2.算法实现
- 3.算法优点
- 4.算法不足
- 三、【一般推荐】方法三:均匀插值等距取样法--均值index原则
- 1.算法原理
- 2.算法实现
- 3.算法优点
- 4.算法不足
- 四、【推荐】方法四:垂直限值法--垂距原则
- 1.算法原理
- 2.算法实现
- 3.算法不足
- 4.算法优点
- 五、【推荐】方法五:道格拉斯-普克(Douglas-Peuker)算法--垂距原则
- 1.算法原理
- 2.算法实现
- 3.算法优点
- 4.算法不足
- 参考资料
- 点到线的距离计算方式--向量法
- 总结
- 参考资料
前言
认知有限,望大家多多包涵,有什么问题也希望能够与大家多交流,共同成长!本文先对路径插值与抽稀篇做个简单的介绍,具体内容后续再更,其他模块可以参考去我其他文章
提示:以下是本篇文章正文内容
一、路径曲线插值、拟合和逼近的区别
因为每种曲线都有其特征,故曲线插值拟合的方法多用在后端局部优化中,大都仅仅适合在车辆转弯,倒车、换道等局部路径中使用,而不能全局路径大范围的使用这种曲线插值拟合的方法,因为曲线性质很难做到全局路径的表达
1、拟合
根据一些离散数据希望得到一个连续的函数(也就是曲线)或者更加密集的离散方程与已知数据相吻合,这过程就叫做拟合
拟合是已知点列,从整体上搞出一条连接已知点列的连续函数(曲线),如最小二乘,最小二乘意义下的拟合,是要求拟合函数与原始数据的均方误差达到极小,是一种整体意义的逼近,对局部性质没有要求
.
.
2、插值
插值是根据已知点列的离散函数,搞出和已知点列函数一样倒是更密集的连续函数
通过拟合得到的函数获得未知点的数据的方法,叫做插值,其中,拟合函数经过所有已知点的插值方法,叫做内插。
“插值”,就是要在原有离散数据之间“插入”一些值,这就要求插值函数必须通过所有的离散点,插值函数在离散点之外的那些点都相当于“插入”的值。插值有全局插值,也有局部插值(比如分段线性插值),插值误差通常考虑的是逐点误差或最大模误差,插值的好坏往往通过某些局部的性质来体现,比如龙格现象或吉布斯振荡
.
.
3、逼近
逼近是已知目标的连续曲线,或者点列,通过逼近使得构造的函数无限靠近它们。使得我现在的数据往已知函数上尽量靠拢
.
.
二、路径点线性插值方法
(1)纯跟踪(pure_persuit)算法内置的插值算法
1.源代码(补充注释了~)
//下一目标线性插值【这种插值方式是根据机器人当前位置和目标插值直线情况进行插值的】
bool PurePursuitController::interpolateNextTarget(int next_waypoint, NavGoal3D& next_target)
{
constexpr double ERROR = pow(10, -5); // 0.00001
int path_size = static_cast<int>(current_waypoints_.size());
if (next_waypoint == path_size - 1)
{
next_target.position = current_waypoints_.at(next_waypoint).position;
return true;
}
double search_radius = lookahead_distance_; //搜索半径的范围是前视距离
NavGoal3D zero_p;
NavGoal3D end = current_waypoints_.at(next_waypoint); //插值终点
NavGoal3D start = current_waypoints_.at(next_waypoint - 1); //插值起点
//假设用二元一次函数直线来拟合,即y=kx+b("ax + by + c = 0")
//给定两个点,待定a,b,c参数,得到一条确定的二元一次函数直线
double a = 0;
double b = 0;
double c = 0;
double get_linear_flag = getLinearEquation(start, end, &a, &b, &c);
if (!get_linear_flag)//插值条件一:参入若不能待定成功
{
return false;
}
// | a * x0 + b * y0 + c |
//圆的半径 d = -------------------------------
// √( a~2 + b~2)
//输入a,b,c即待定了目标拟合的直线
//输入机器人现在的位姿current_pose_,计算机器人现在的位姿与目标拟合的直线的距离d
double d = getDistanceBetweenLineAndPoint(current_pose_, a, b, c);
if (d > search_radius) //插值条件二:若机器人现在的位姿与目标拟合的直线的距离d大于前视距离【这种插值方式是根据机器人当前位置和目标插值直线情况进行插值的】
{
return false;
}
Eigen::Vector3d v((end.position(0) - start.position(0)), (end.position(1) - start.position(1)), 0);//定义“起点”到“终点”的向量v
Eigen::Vector3d unit_v = v.normalized(); //向量单位化unit_v
Eigen::Vector3d unit_w1 = rotateUnitVector(unit_v, 90); //单位向量unit_v顺时针旋转90度
Eigen::Vector3d unit_w2 = rotateUnitVector(unit_v, -90);//单位向量unit_v逆时针旋转90度
//计算以current_pose_为中心圆半径与目标直线垂线的上交点h1
NavGoal3D h1;
h1.position(0) = current_pose_.position(0) + d * unit_w1[0];
h1.position(1) = current_pose_.position(1) + d * unit_w1[1];
h1.position(2) = current_pose_.position(2);
//计算以current_pose_为中心圆半径与目标直线垂线的下交点h2
NavGoal3D h2;
h2.position(0) = current_pose_.position(0) + d * unit_w2[0];
h2.position(1) = current_pose_.position(1) + d * unit_w2[1];
h2.position(2) = current_pose_.position(2);
// ROS_INFO("error : %lf", error);
// ROS_INFO("whether h1 on line : %lf", h1.y - (slope * h1.x + intercept));
// ROS_INFO("whether h2 on line : %lf", h2.y - (slope * h2.x + intercept));
//插值条件三:检查垂线的两交点中的哪一交点在直线方程上
NavGoal3D h;
if (fabs(a * h1.position(0) + b * h1.position(1) + c) < ERROR) //上交点交于直线方程上
{
h.position = h1.position;
// ROS_INFO("use h1");
}
else if (fabs(a * h2.position(0) + b * h2.position(1) + c) < ERROR)//下交点交于直线方程上
{
// ROS_INFO("use h2");
h.position = h2.position;
}
else //上下交点都不交于直线方程上
{
return false;
}
if (d == search_radius) //若机器人现在的位姿与目标拟合的直线的距离d等于前视距离
{
next_target.position = h.position;
return true;
}
else //若机器人现在的位姿与目标拟合的直线的距离d小于前视距离(大于的情况上面已经挂了)
{
double s = sqrt(pow(search_radius, 2) - pow(d, 2)); //计算插值距离,使用的是勾股定理
NavGoal3D target1;//第一个插值点(前面)
target1.position(0) = h.position(0) + s * unit_v[0];
target1.position(1) = h.position(1) + s * unit_v[1];
target1.position(2) = current_pose_.position(2);
NavGoal3D target2; //第二个插值点(后面)
target2.position(0) = h.position(0) - s * unit_v[0];
target2.position(1) = h.position(1) - s * unit_v[1];
target2.position(2) = current_pose_.position(2);
// 检查target1、target2交点是否在终点和起点之间
double interval = getPlaneDistance(end, start); //current_waypoints_前后两个点的距离
if (getPlaneDistance(target1, end) < interval)
{
// ROS_INFO("result : target1");
next_target.position = target1.position;
return true;
}
else if (getPlaneDistance(target2, end) < interval)
{
// ROS_INFO("result : target2");
next_target.position = target2.position;
return true;
}
else
{
// ROS_INFO("result : false ");
return false;
}
}
}
2.插值原理解释

步骤:
(1)先通过两个目标插值的两个点待定一条二元一次直线方程的参数
(2)以机器人当前位姿为圆心,计算机器人与直线方程垂线的距离,该距离小于最小前视距离才符合pure_persuit算法更新点的逻辑,进而才会插值
(3)根据前视距离和垂线距离为两个直角边,通过勾股定理计算出第三边,并把第三遍投影到直线方程ax+by+c=0上,得到插值的target点
(4)检查插值的target点到end点的距离,要小于start点到end点的距离,才可以插值成功【防盗标记–盒子君hzj】
要调节的参数
(1)前视距离lookahead_distance
(2)原始两个点的距离【防盗标记–盒子君hzj】
3.算法优点
插值不仅仅考虑了原本的路径点本身,也考虑了机器人当前的位姿
4.算法缺点
只能两点插值,并适配pure_persuit算法
.
.
(2)纯跟踪(pure_persuit)的虚拟点补偿插值算法
1.示例图

2.代码实现
// //把扩展的车道的起点和航线的起点连接在一起
void PurePursuitController::connectVirtualLastWaypoints(std::vector<NavGoal3D> & lane, LaneDirection direction)
{
//判断扩展车道的起点有没有给到,没有给到就不用连接了
if (lane.empty())
{
return;
}
static double interval = 0.5; //设置路径连接的间隔点为0.5米
//设置最后一个点位置、姿态。姿态这里要yaw转四元素!!!(因为表示不统一的问题)
NavGoal3D pn;
pn.position = lane.back().position;
Eigen::Vector3d euler(0,0,lane.back().yaw);
Eigen::Quaterniond Q1;
Q1 = Euler2Quaternion(euler);
lane.back().orientation.x = Q.x();
lane.back().orientation.y = Q.y();
lane.back().orientation.z = Q.z();
lane.back().orientation.w = Q.w();
pn.orientation = lane.back().orientation;
//设置要虚拟增加的一个点(仅仅有位置、方向、速度信息)
NavGoal3D virtual_last_waypoint;
virtual_last_waypoint.orientation = pn.orientation;
virtual_last_waypoint.speed = 0.0;
//插值点的中间变量
NavGoal3D virtual_last_point_rlt;
const int sgn = getSgn(); //设置前进、后退方向
for (double dist = minimum_lookahead_distance_; dist > 0.0; dist -= interval) //开始连接【最小前视距离内进行插值一堆点,插值密度是interval】
{
virtual_last_point_rlt.position(0) += interval * sgn; //位置增量
virtual_last_waypoint.position = // 设置设置虚拟增加点的位置
calcAbsoluteCoordinate(virtual_last_point_rlt, pn).position; //输入最后一个点位置,及其它的位置增量,计算虚拟插值的点的位置
lane.emplace_back(virtual_last_waypoint);
}
}
//输入最后一个点位置,及其它的位置增量,计算虚拟插值的点的位置
xag_nav::common::NavGoal3D PurePursuitController::calcAbsoluteCoordinate(NavGoal3D &point_msg, NavGoal3D ¤t_pose)
{
//四元数
Eigen::Quaterniond q1 = Eigen::Quaterniond(current_pose.orientation.w, current_pose.orientation.x,
current_pose.orientation.y, current_pose.orientation.z).normalized();
Eigen::Quaterniond q2 = Eigen::Quaterniond(1, 0, 0, 0).normalized();
//平移向量
Eigen::Vector3d t1 = Eigen::Vector3d(current_pose.position(0), current_pose.position(1), current_pose.position(2));
Eigen::Vector3d t2 = Eigen::Vector3d(0, 0, 0);
//目标向量
Eigen::Vector3d p1 = Eigen::Vector3d(point_msg.position(0), point_msg.position(1), point_msg.position(2));
Eigen::Vector3d p2;
//四元数求解
p2 = q2 * q1.inverse() * (p1 - t1) + t2;
//std::cout << p2.transpose() << std::endl;
//欧拉矩阵
Eigen::Isometry3d T1 = Eigen::Isometry3d::Identity();
Eigen::Isometry3d T2 = Eigen::Isometry3d::Identity();
T1.rotate(q1.toRotationMatrix());
T1.pretranslate(t1);
T2.rotate(q2.toRotationMatrix());
T2.pretranslate(t2);
// std::cout << T1.matrix() << std::endl;
// std::cout << T2.matrix() << std::endl;
//欧拉矩阵求解
p2 = T1 * T2.inverse() * p1;
// std::cout << p2.transpose() << std::endl;
//xag_nav_msgs::Point tf_point_msg;
NavGoal3D tf_point_msg;
tf_point_msg.position(0) = p2[0];
tf_point_msg.position(1) = p2[1];
tf_point_msg.position(2) = p2[2];
return tf_point_msg;
}
(3)普通的线性插值算法
1.源代码(补充注释了~)
// 路径插值
//注意输入的wps可以是两个点,也可以是很多点
//wps 仅仅包含(x,y,z,yaw)
std::vector<common::NavGoal3D> Seg_cruise_section::fixPathDensity(std::vector<NavGoal3D> &wps, float resolution)
{
float _pathResolution = resolution; //设置分辨率
if (wps.size() == 0 || _pathResolution == 0) //若输入的路径点为0,或者插值的分辨率为0
{
return wps;
}
double dis = 0, ang = 0;
double margin = _pathResolution * 0.01;
double remaining = 0;
int nPoints = 0;
std::vector<NavGoal3D> fixedwps; //定义插值后的路径点
fixedwps.assign(wps.begin(),wps.end()); //把原始的点加入进来,只是为了确定vector的大小
fixedwps.clear();
fixedwps.push_back(wps.at(0)); //设置插值第一个点
//开始插值
size_t start = 0, next = 1;
while (next <wps.size())
{
//计算两个路径点之间的距离dis和角度ang
dis += hypot(wps[next].position(0) - wps[next-1].position(0), wps[next].position(1) - wps[next-1].position(1))+ remaining;
ang = atan2(wps[next].position(1) - wps[start].position(1), wps[next].position(0) - wps[start].position(0));
if (dis < _pathResolution - margin) //若两个路径点之间的距离小于阈值,该点不用进行插值了
{
next++;
remaining = 0;
}
else if (dis > (_pathResolution + margin)) //若两个路径点之间的距离大于阈值,该点进行插值
{
NavGoal3D point_start = wps[start];
nPoints = dis / _pathResolution; //计算要插入的路径点数量
for (int j = 0; j < nPoints; j++)
{
//位置xy
point_start.position(0) = point_start.position(0) + _pathResolution * cos(ang);
point_start.position(1) = point_start.position(1) + _pathResolution * sin(ang);
//yaw的欧拉角转四元素--方向【这里或许不兼容】(但是跟踪来说不用姿态)
//解决办法1:控制器用的时候再把四元素转成欧拉yaw角
//解决办法2:在这里直接用ang代表yaw就行
Eigen::AngleAxisd rollangle(0, Eigen::Vector3d::UnitX());
Eigen::AngleAxisd yawangle(ang, Eigen::Vector3d::UnitZ());
Eigen::AngleAxisd pitchangle(0, Eigen::Vector3d::UnitY());
Eigen::Quaterniond q = rollangle * yawangle * pitchangle;
point_start.orientation.x= q.x();
point_start.orientation.y = q.y();
point_start.orientation.z = q.z();
point_start.orientation.w = q.w();
fixedwps.push_back(point_start);
}
remaining = dis - nPoints * _pathResolution;
start++;
wps[start].position = point_start.position;
dis = 0;
next++;
}
else { ///若两个路径点之间的距离等于阈值,该点进行插值
dis = 0;
remaining = 0;
fixedwps.push_back(wps[next]);
next++;
start = next - 1;
}
}
return fixedwps;
}
2.源代码解释

步骤:
(1)判断要插值的两个点是否小于插值距离的分辨率,若是就不要进行插值了
(2)根据要插值的两个点距离dis和插值距离的分辨率,计算在两点之间要插入多少个点npoints
(3)根据插值分辨率大小和方式,从头到尾一个一个点进行插值【防盗标记–盒子君hzj】
3.算法优点
(1)实现简单
(2)可以输入一堆点进行插值
4.算法缺点
插值仅仅考虑了路径本身,【防盗标记–盒子君hzj】没有考虑机器人当前状态咯
(4)y0和yf之间的线性插值(x在0和1之间)
template <typename y_t, typename x_t>
y_t lerp(y_t y0, y_t yf, x_t x)
{
static_assert(std::is_floating_point<x_t>::value,
"must use floating point value");
assert(x >= 0 && x <= 1);
return y0 + (yf - y0) * x;
}
总结
线性插值是用一系列首尾相连的线段依次连接相邻各点
线性插值的特点是计算简便,但光滑性很差。如果用线性插值拟合一条光滑曲线,对每一段线段,原曲线在该段内二阶导数绝对值的最大值越大,拟合的误差越大。
一次多项式就是直线拟合算法。常用的又线性差值算法和双线性差值算法
参考资料
线性插值
https://blog.csdn.net/u010312937/article/details/82055431
双线性插值
https://blog.csdn.net/eric_e/article/details/79499617
https://zhuanlan.zhihu.com/p/22882367
.
.
三、常用的路径抽稀算法
抽稀的定义
在处理矢量化数据时,记录中往往会有很多重复数据,对进一步数据处理带来诸多不便。多余的数据一方面浪费了较多的存储空间,另一方面造成所要表达的图形不光滑或不符合标准。因此要通过某种规则,在保证矢量曲线形状不变的情况下, 最大限度地减少数据点个数,这个过程称为抽稀。
通俗的讲就是对曲线进行采样简化,即在曲线上取有限个点,将其变为折线,并且能够在一定程度保持原有形状。比较常用的两种抽稀算法是:道格拉斯-普克(Douglas-Peuker)算法和垂距限值法。
抽稀因子的核心思想
曲线抽稀的关键是定义抽稀因子,抽稀因子的不同决定的抽稀算法的多样性,在现有抽稀理论中,有按步长,线段长度,垂距等来定义抽稀因子。
一、方法一:步长距离法–步长原则
1.算法原理
步长法是沿连续曲线每隔一定的步长距离抽取一点,其余点全部压缩掉,然后在相邻抽取点间用直线连续或曲线拟合逼近。
2.算法实现
实现较为简单,自己编程
3.算法优点
原理及实现简单,通用行较强,单算法效果不佳
4.算法不足
一,【转弯丢特征】曲线上的特征点,如曲线拐弯处,曲线变化较大的点可能因抽稀被压缩掉,导致曲线变形;因此,抽取后的曲线与原曲线有一定的误差,误差大小与步长的设置及曲线拟合方法有关。
二,【直线多冗余的点】在某些情况下,仍会留下部分多余点无法删除,如曲线中有一段比较直,而步长又较小,会导致此段直线上有多个抽取点,而实际上只要保留直线段的首尾点即可
面对特征不同的路径点,算法参数对抽稀效果影响较大,表现差异较大。换句话说,算法的效果泛化能力较差
.
.
二、方法二:线段过滤法–线段长度原则
1.算法原理
当某一段路径的长度小于某一阈值时,就以该段的中点代替该段,此段路径的两端退化到中点一样。线段过滤法和步长距离法一样,阈值的大小决定着抽稀算法的精度,一般也是由编程人员自行确定。
2.算法实现
实现较为简单,自己编程
3.算法优点
原理及实现简单,通用行较强,但算法效果不佳,但是比距离步长法要好
4.算法不足
算法参数对抽稀效果影响较大,算法的效果泛化能力较差
三、【一般推荐】方法三:均匀插值等距取样法–均值index原则
1.算法原理
先进行使用线性插值算法进行等距插值,再进行均匀ID抽稀,把插值和抽稀两个步骤集成在一起,先设置等距插值的分辨率,在进行均匀路径点ID抽稀,一般是二抽一
路径点抽稀分辨率=路径点插值分辨率/2
2.算法实现
实现较为简单,自己编程
3.算法优点
这种方法原理设计上比较保守,但算法的稳定性较强,原理也相对简单,调好参数即可
4.算法不足
算法同时使用了路径插值和路径抽稀,然而这两者是互斥的,增大了算法的时间复杂度和空间复杂度
.
.
四、【推荐】方法四:垂直限值法–垂距原则
1.算法原理
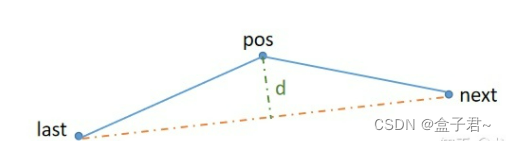
从第一点开始依次筛选,去除冗余点。即以第一点为起点,计算第二点至第一点和第三点连线的垂直距离,若此距离大于某阈值,则保留第二点,并将其作为新起点,计算第三点至第二点和第四点连线的距离;否则,去除第二点,计算第三点至第一点和第四点连线距离,依次类推,直至曲线上最后一点。其阈值一般取相应地物最大允许误差或更小
2.算法实现
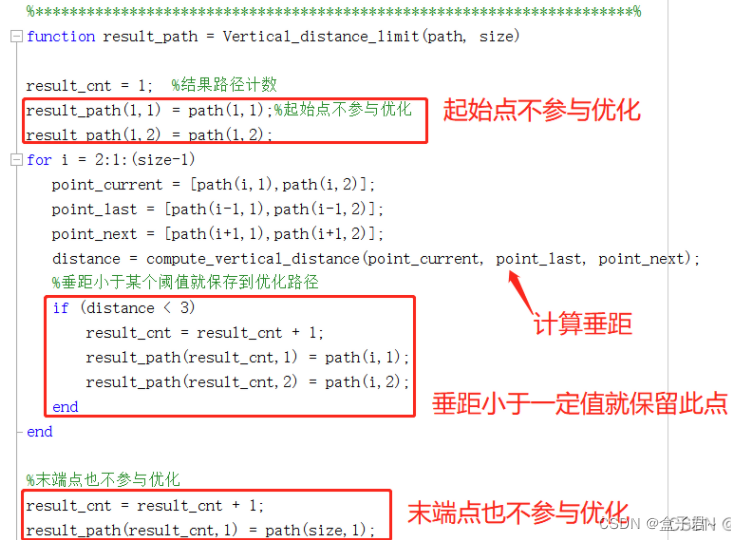
算法过程如下:
以第二个点开始,计算第二个点到前一个点和后一个点所在直线的距离d;
如果d大于阈值,则保留第二个点,计算第三个点到第二个点和第四个点所在直线的距离d;
若d小于阈值则舍弃第二个点,计算第三个点到第一个点和第四个点所在直线的距离d;
依次类推,直线曲线上倒数第二个点。
# -*- coding: utf-8 -*-
"""
-------------------------------------------------
File Name: LimitVerticalDistance
Description : 垂距限值抽稀算法
Author : J_hao
date: 2017/8/17
-------------------------------------------------
Change Activity:
2017/8/17:
-------------------------------------------------
"""
from __future__ import division
from math import sqrt, pow
__author__ = 'J_hao'
THRESHOLD = 0.0001 # 阈值
"""
计算点a到点b c所在直线的距离
:param point_a:
:param point_b:
:param point_c:
:return:
"""
def point2LineDistance(point_a, point_b, point_c):
# 首先计算b c 所在直线的斜率和截距
if point_b[0] == point_c[0]:
return 9999999
slope = (point_b[1] - point_c[1]) / (point_b[0] - point_c[0])
intercept = point_b[1] - slope * point_b[0]
# 计算点a到b c所在直线的距离
distance = abs(slope * point_a[0] - point_a[1] + intercept) / sqrt(1 + pow(slope, 2))
return distance
# 垂直限值抽稀算法的实现
class LimitVerticalDistance(object):
def __init__(self):
self.threshold = THRESHOLD # 限值参数
self.qualify_list = list() # 输出的抽稀路径
"""
抽稀
:param point_list:二维点列表
:return:
"""
def diluting(self, point_list):
self.qualify_list.append(point_list[0]) # 初始化抽稀列表
check_index = 1
# 遍历路径上第二个点到倒数第二个点,进行抽稀
while check_index < len(point_list) - 1:
# 计算路径上不相邻的两个点组成的直线与第三个点的距离
distance = point2LineDistance(point_list[check_index],
self.qualify_list[-1],
point_list[check_index + 1])
# 若距离不超过最大阈值,继续遍历
if distance < self.threshold:
check_index += 1
#若距离超过最大阈值,把该点存入抽稀路径中,并一该点为新的起点进行新一轮遍历
else:
self.qualify_list.append(point_list[check_index])
check_index += 1
return self.qualify_list
if __name__ == '__main__':
l = LimitVerticalDistance()
diluting = l.diluting([[104.066228, 30.644527], [104.066279, 30.643528], [104.066296, 30.642528], [104.066314, 30.641529],
[104.066332, 30.640529], [104.066383, 30.639530], [104.066400, 30.638530], [104.066451, 30.637531],
[104.066468, 30.636532], [104.066518, 30.635533], [104.066535, 30.634533], [104.066586, 30.633534],
[104.066636, 30.632536], [104.066686, 30.631537], [104.066735, 30.630538], [104.066785, 30.629539],
[104.066802, 30.628539], [104.066820, 30.627540], [104.066871, 30.626541], [104.066888, 30.625541],
[104.066906, 30.624541], [104.066924, 30.623541], [104.066942, 30.622542], [104.066960, 30.621542],
[104.067011, 30.620543], [104.066122, 30.620086], [104.065124, 30.620021], [104.064124, 30.620022],
[104.063124, 30.619990], [104.062125, 30.619958], [104.061125, 30.619926], [104.060126, 30.619894],
[104.059126, 30.619895], [104.058127, 30.619928], [104.057518, 30.620722], [104.057625, 30.621716],
[104.057735, 30.622710], [104.057878, 30.623700], [104.057984, 30.624694], [104.058094, 30.625688],
[104.058204, 30.626682], [104.058315, 30.627676], [104.058425, 30.628670], [104.058502, 30.629667],
[104.058518, 30.630667], [104.058503, 30.631667], [104.058521, 30.632666], [104.057664, 30.633182],
[104.056664, 30.633174], [104.055664, 30.633166], [104.054672, 30.633289], [104.053758, 30.633694],
[104.052852, 30.634118], [104.052623, 30.635091], [104.053145, 30.635945], [104.053675, 30.636793],
[104.054200, 30.637643], [104.054756, 30.638475], [104.055295, 30.639317], [104.055843, 30.640153],
[104.056387, 30.640993], [104.056933, 30.641830], [104.057478, 30.642669], [104.058023, 30.643507],
[104.058595, 30.644327], [104.059152, 30.645158], [104.059663, 30.646018], [104.060171, 30.646879],
[104.061170, 30.646855], [104.062168, 30.646781], [104.063167, 30.646823], [104.064167, 30.646814],
[104.065163, 30.646725], [104.066157, 30.646618], [104.066231, 30.645620], [104.066247, 30.644621], ])
print len(diluting)
print(diluting)
下面的可以参考
https://blog.csdn.net/morgerton/article/details/60878302
3.算法不足
按照垂直距离进行抽稀,主要考虑的是局部曲线的特性–对于曲率变化较大的路径有效,长直线几乎没有抽稀效果
4.算法优点
垂距限值法与DP算法原理一样,但其并非从整体角度考虑一条完整曲线,而是从局部角度考虑
易于理解及实现且通用性比较强!
.
.
五、【推荐】方法五:道格拉斯-普克(Douglas-Peuker)算法–垂距原则
1.算法原理
(1)算法理论
DP抽稀理论是Douglas,Peucker二人在1973年发表的文章《Algorithms for the reduction of the number of points required to represent a digitized line or itsCaricature 》提出的方法。简而言之就是用直线替代曲线。选取一段曲线,曲线的两个端点连线作一条直线,如果曲线上所有点到这条直线的垂直距离小于阈值,那么就用这条端点连线的直线替代曲线,去掉中间的所有点。在按顺序检查的过程中,如果有某一个点的垂直距离大于阈值,那么保留住这个点,以这个点为新的端点,连接最初的两个端点,继续考察垂直距离。重复第一步的操作,用以确定保留或者抽去中间点。

值得一提的是,Konrad Ebisch在2002年发表的文章《A correction to the Douglas-Peucker line generalization algorithm》提出了DP的这种方法在垂距小于阈值时容易出现计算错误。而后,又有Dan Sunday、胡涛等人提出分区计算距离度量的方法来改进DP算法。
(2)算法步骤如下
- 将轨迹的首尾点连成一条线,计算曲线上每一个点到直线的距离,找出最大距离dmax,看距离是否小于给定的阈值max(及轨迹精确度)。
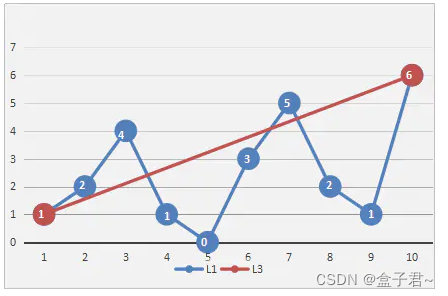
- a.若dmax < max,则舍弃这条曲线上的所有中间点,将曲线首尾点连成的直线作为这段曲线的近似,这条线段便处理完毕。(这个条件的目的是滤除特征相近的路径点)
b.若dmax >= max,则以dmax所在点作为分割点,将原来的曲线分为两段,分出来的两条曲线继续直线步骤1、2,直到所有的dmax < max。(这个条件的目的是保持特征不同的路径点)
特征的区别度表征就是阈值dmax
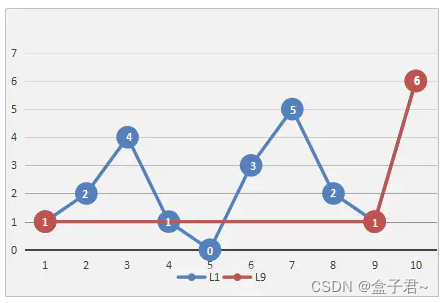
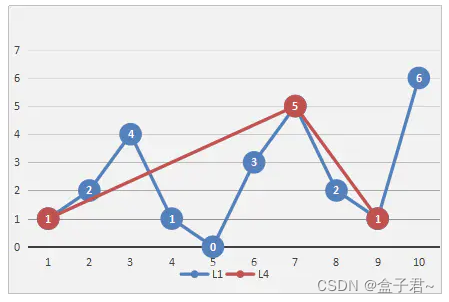
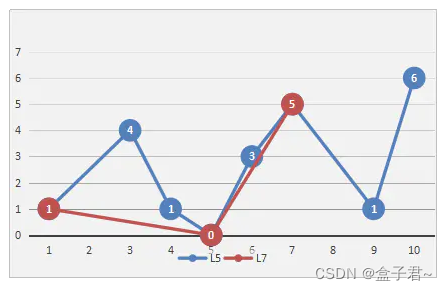
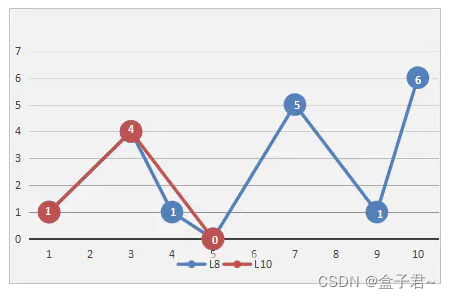
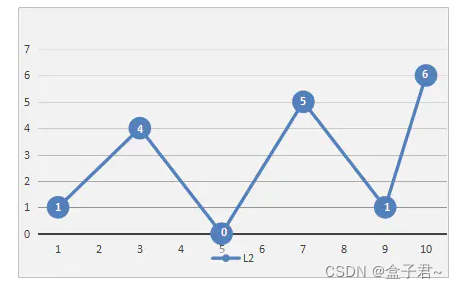
显然,算法的抽稀精读是和阈值相关的,阈值越大,舍弃的点越多,提取的关键点越少。若绘制的轨迹较长,可在对地图进行缩放时动态调整阈值
在opencv中,轮廓近似函数就是用该算法实现的
cv2.approxPolyDP(cnt, eps,True)
2.算法实现
伪代码如下:
1、连接曲线首尾两点A、B;
2、依次计算曲线上所有点到A、B两点所在曲线的距离;
3、计算最大距离D,如果D小于阈值threshold,则去掉曲线上出A、B外的所有点;如果D大于阈值threshold,则把曲线以最大距离分割成两段;
4、对所有曲线分段重复1-3步骤,知道所有D均小于阈值。即完成抽稀。
/**
* gps轨迹抽稀算法
* @author: Z1hgq
*/
/**
* 点到直线的距离,直线方程为 ax + by + c = 0
* @param {Number} a 直线参数a
* @param {Number} b 直线参数b
* @param {Number} c 直线参数c
* @param {Object} xy 点坐标例如{ lat: 2, lng: 2 }
* @return {Number}
*/
function getDistanceFromPointToLine(a, b, c, xy) {
const x = xy.lng;
const y = xy.lat;
return Math.abs((a * x + b * y + c) / Math.sqrt(a * a + b * b));
}
/**
* 根据两个点求直线方程 ax+by+c=0
* @param {Object} xy1 点1,例如{ lat: 1, lng: 1 }
* @param {Object} xy2 点2,例如{ lat: 2, lng: 2 }
* @return {Array} [a,b,c] 直线方程的三个参数
*/
function getLineByPoint(xy1, xy2) {
const x1 = xy1.lng; // 第一个点的经度
const y1 = xy1.lat; // 第一个点的纬度
const x2 = xy2.lng; // 第二个点的经度
const y2 = xy2.lat; // 第二个点的纬度
const a = y2 - y1;
const b = x1 - x2;
const c = (y1 - y2) * x1 - y1 * (x1 - x2);
return [a, b, c];
}
/**
* 稀疏点
* @param {Array} points 参数为[{lat: 1, lng: 2},{lat: 3, lng: 4}]点集
* @param {Number} max 阈值,越大稀疏效果越好但是细节越差
* @return {Array} 稀疏后的点集[{lat: 1, lng: 2},{lat: 3, lng: 4}],保持和输入点集的顺序一致
*/
//输入一条路径,和阈值
function sparsePoints(points, max) {
//如果输入的路径点只有一个点或者两个点,无法插值,直接返回
if (points.length < 3) {
return points;
}
const xy1 = points[0]; // 获取路径的第一个点
const xy2 = points[points.length - 1]; //获取路径的最后一个点
const [a, b, c] = getLineByPoint(xy1, xy2); // 输入路径首尾两个点,获取直线方程的a,b,c值
let ret = []; // 输出的稀疏以后的路径
let dmax = 0; // 记录点到直线的最大距离
let split = 0; // 路径分割位置
//从第二个点到倒数第二个点,对路径进行抽稀处理
for (let i = 1; i < points.length - 1; i++) {
const d = getDistanceFromPointToLine(a, b, c, points[i]);//计算点到线的距离
//遍历整条路径上的路径点,得到离首尾直线距离最远的路径点,并记录其ID
if (d > dmax) {
split = i;
dmax = d;
}
}
// 如果存在点到首位点连成直线的距离大于max的,即需要再次划分
if (dmax > max) {
// 按split分成左边一条路径,再递归,返回稀疏后的前后两个点
const child1 = sparsePoints(points.slice(0, split + 1), max);
// 按split分成右边一条路径,再递归,返回稀疏后的前后两个点
const child2 = sparsePoints(points.slice(split), max);
// 因为child1的最后一个点和child2的第一个点,肯定是同一个(即为分割点),合并的时候,需要注意一下
ret = ret.concat(child1, child2.slice(1));
return ret;
} else {
// 如果不存在点到直线的距离大于阈值的,那么就直接是首尾点了
return [points[0], points[points.length - 1]];
}
}
export default sparsePoints;
【上面python的设计架构不错,直接改成C++就好】
C++语言的实现【这个架构不太好】
//计算两点距离
double Distance(int x1, int y1, int x2, int y2) {
double distance;
distance =
(double)sqrt(double(x2 - x1) * (x2 - x1) + (y2 - y1) * (y2 - y1));
return distance;
}
//点到线的距离
double NDistance(int x1, int y1, int x2, int y2, int x3, int y3) {
double A = y1 - y2;
double B = x2 - x1;
int C = -B * y1 - A * x1;
double ndistance =
fabs(float(A * x3 + B * y3 + C)) / sqrt(pow(A, 2) + pow(B, 2));
return ndistance;
}
// Douglas一Peukcer算法
//输入一条左边路径pVector
//输入一条右边路径pVector
//阈值
void CMyDoc::getNDistance(vector<pair<int, int>>::iterator pVector,
vector<pair<int, int>>::iterator pVector1,
int limit) {
//定义三条路径
vector<pair<int, int>>::iterator testVector;
vector<pair<int, int>>::iterator testVector1; // 路径分割位置
vector<pair<int, int>>::iterator tempVector;
tempVector = pVector;
//如果右边的路径起点等于左边路径终点,即输入的总路径只有一个或者两个点,不能抽稀,直接退出!
if (pVector1 == (tempVector++)) return;
double MaxDistance = 0.0; // 记录点到直线的最大距离
//从第二个点到倒数第二个点,对路径进行抽稀处理
for (tempVector; tempVector != pVector1;) {
testVector = (tempVector++);
//计算点到线的距离
double temp;
temp = NDistance((*pVector).first, (*pVector).second, (*pVector1).first,
(*pVector1).second, (*testVector).first,
(*testVector).second);
//遍历整条路径上的路径点,得到离首尾直线距离最远的路径点,并记录其ID
if (MaxDistance < temp) {
MaxDistance = temp; // 记录点到直线的最大距离
testVector1 = testVector; //记录分割的位置
}
}
tempVector = pVector;
//点到线的距离小于阈值
if (MaxDistance < limit) {
for (tempVector++; tempVector != pVector1; tempVector++) {
(*tempVector).first = 8080;
(*tempVector).second = 8080;
// point.erase(pVector);
}
return;
}
//点到线的距离大于阈值,继续迭代
getNDistance(pVector, testVector1, limit); //迭代
getNDistance(testVector1, pVector1, limit);
}
下面这个有用
https://blog.csdn.net/wjl_zyl_1314/article/details/109624604
https://blog.csdn.net/my_lord_/article/details/49980091
https://github.com/Nidcoco/DouglasPeuckerDemo
3.算法优点
综合全局整体曲线,同时兼顾局部曲线特性的方法–通用性较强且效果相对较好
Douglas-Peuker正是一个对坐标关键点进行抽取的算法。录制的轨迹要有顺序,但是对路径点的距离要求可以是不均匀的!
4.算法不足
实现步骤简单,但是算法的空间复杂度较高,每次分割折线都要遍历一次范围内的节点
参考资料
【路径规划】使用垂距限值法与贝塞尔优化A星路径
https://blog.csdn.net/a_xiaoning/article/details/125625627
https://zhuanlan.zhihu.com/p/473463671
https://baike.baidu.com/item/%E6%8A%BD%E7%A8%80/7297123?fr=aladdin
https://www.cnblogs.com/mosquito18/p/10113096.html
点到线的距离计算方式–向量法
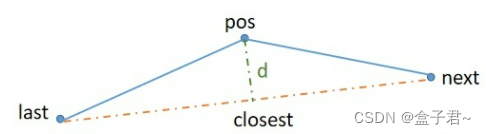
使用向量法计算垂距的步骤可以按照如下来进行:
1) 先计算向量last_to_next的单位向量u_last_to_next
2) 计算向量last_to_pos,之后计算last_to_pos与向量u_last_to_next的点乘,即为last_to_pos到向量u_last_to_next上的投影长度L
3) 使用向量u_last_to_next乘以L即为向量last_to_closest
4) 使用last的坐标加上last_to_closest即可求出closest的坐标
5) 之后就可以求出pos与closest的距离
.
.
使用几何法计算垂距的步骤可以按照如下来进行:
点到直线距离可以用公式求出,直线方程,可用两点式求出
1)先求出直线两点式 为 (y-y0)/(y2-y0 )= (x-x0)/(x2-x0) 整理成标准 形式 Ax +By+C =0
手动整理出来公式
程序中,用整理出来的公式,求出 A,B,C
2)运用点到直线距离公式
d =fabs(A x +B y +C) /sqrt(A*A +B*B)
/**
* 根据两个点求直线方程 ax+by+c=0
* @param {Object} xy1 点1,例如{ lat: 1, lng: 1 }
* @param {Object} xy2 点2,例如{ lat: 2, lng: 2 }
* @return {Array} [a,b,c] 直线方程的三个参数
*/
function getLineByPoint(xy1, xy2) {
const x1 = xy1.lng; // 第一个点的经度
const y1 = xy1.lat; // 第一个点的纬度
const x2 = xy2.lng; // 第二个点的经度
const y2 = xy2.lat; // 第二个点的纬度
const a = y2 - y1;
const b = x1 - x2;
const c = (y1 - y2) * x1 - y1 * (x1 - x2);
return [a, b, c];
}
//点到线的距离
double NDistance(int x1, int y1, int x2, int y2, int x3, int y3) {
double A = y1 - y2;
double B = x2 - x1;
int C = -B * y1 - A * x1;
double ndistance =
fabs(float(A * x3 + B * y3 + C)) / sqrt(pow(A, 2) + pow(B, 2));
return ndistance;
}
def point2LineDistance(point_a, point_b, point_c):
"""
计算点a到点b c所在直线的距离
:param point_a:
:param point_b:
:param point_c:
:return:
"""
# 首先计算b c 所在直线的斜率和截距
if point_b[0] == point_c[0]:
return 9999999
slope = (point_b[1] - point_c[1]) / (point_b[0] - point_c[0])
intercept = point_b[1] - slope * point_b[0]
# 计算点a到b c所在直线的距离
distance = abs(slope * point_a[0] - point_a[1] + intercept) / sqrt(1 + pow(slope, 2))
return distance






![[CISCN2019 华北赛区 Day1 Web2]ikun](https://img-blog.csdnimg.cn/fbdd8952efec48fab93a5af5f40c911b.png)