循环链表+双向链表
循环链表
循环链表是头尾相接的链表(即表中最后一个结点的指针域指向头结点,整个链表形成一个环)(circular linked list)

**优点:**从表中任一结点出发均可访问全部结点
循环链表与单链表的主要差别当链表遍历时,判别当前指针p是否指向表尾结点的终止条件不同。在单链表中,判别条件为p!=NULL或p->next=NULL,而循环单链表的判别条件为p!=L或p->next!=L




#include<stdio.h>
#include<stdlib.h>
typedef struct Lnode {
int data;
struct Lnode* next;
}Lnode,*LinkList;
/*初始化循环单链表*/
Lnode* InitList(LinkList L)
{
L = (Lnode*)malloc(sizeof(Lnode));
if (L == NULL)
{
//提示分配失败
}
L->next = L;
}
//判断循环单链表是否为空 (终止条件为p或p->next是否等于头指针)
int Isempty(LinkList L)
{
if (L->next == L)
{
return 1;
}
else {
return -1;
}
}
//判断结点p是否为循环单链表的表尾结点
int isTail(LinkList L, Lnode* p)
{
if (p->next == L)
{
return 1;
}
else {
return -1;
}
}
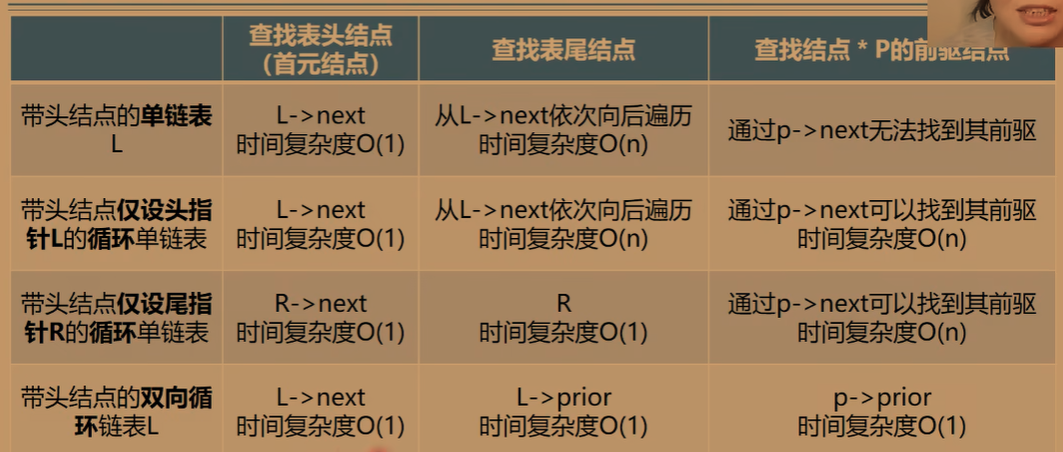
单链表和循环单链表的比较:
**单链表:**从一个结点出发只能找到该结点后续的各个结点;对链表的操作大多都在头部或者尾部;设立头指针,从头结点找到尾部的时间复杂度=O(n),即对表尾进行操作需要O(n)的时间复杂度;
**循环单链表:**从一个结点出发,可以找到其他任何一个结点;设立尾指针,从尾部找到头部的时间复杂度为O(1),即对表头和表尾进行操作都只需要O(1)的时间复杂度;
双向链表

为了克服单链表的这一缺点,老科学家们设计了双向链表(double linked list)是在单链表的每个结点中再设计一个指向其前驱结点的指针域。所以在双向链表中的结点有两个指针域,一个指向直接后继,另一个指向直接前驱。这样链表中有两个不同方向的链。


与单循环链表类似双向链表也可以有循环表(首尾相接形成"环"[2个])
让头结点的前驱指针指向链表的最后一个结点
最后一个结点的后继指针指向头结点

双向链表结构有对称性(设指针p指向某一个结点)
p->prior->next=p=p->next->prior(前进一步后退一步相当于原地踏步)
在双向链表中有些操作(ListLength,GetElemment等因为只涉及一个方向的指针他们的算法与线性表的相同)但在插入和删除需要修改两个方向上的指针两者的算法复杂度均为O(n)
双向链表的插入


单链表只需修改两个指针,而双向链表修改四个指针
算法复杂度O(n)

总结
链式存储结构的优点:
-
结点空间可以动态申请和释放;
-
数据元素的逻辑次序靠结点的指针来指示,插入和删除不需要移动元素。
链式存储结构的缺点:
-
存储密度小,每个结点的指针域需额外占用存储空间。当每个结点的数据域所占的字节数不多时,指针域所占的存储空间的比重显得很大。
-
存储密度是指结点数据本身占用的空间**/结点占用的空间总量**

链式存储结构是非随机存取结构。对任一结点的操作都要从头指针依指针链查找到该结点,这增加了算法的复杂度。(对某个结点操作一般要先找到该结点)

代码总结
双向链表
#include<stdio.h>
#include<stdlib.h>
typedef struct Lnode {
int data; //数据域
struct Lnode* prior, * next; //前驱和后继指针
}DLnode,*DLinkList;
DLnode* InitDLinkList(DLinkList L)
{
L = (DLnode*)malloc(sizeof(DLnode));
if (L == NULL)
{
return -1; //分配失败
}
else
{
L->prior = NULL; //头指针的前驱指针永远指向NULL
L->next = NULL;
}
return L;
}
void InsertNextDLnode(DLnode* p, DLnode* s) { //将结点 *s 插入到结点 *p之后
if (p == NULL || s == NULL) //非法参数
return;
s->next = p->next;
if (p->next != NULL) //p不是最后一个结点=p有后继结点
p->next->prior = s;
s->prior = p;
p->next = s;
return;
}
/*
按位序插入操作:
思路:从头结点开始,找到某个位序的前驱结点,对该前驱结点执行后插操作;
前插操作:
思路:找到给定结点的前驱结点,再对该前驱结点执行后插操作;*/
/*删除*/
/*删除p结点的后继结点*/
void DeleteDLnode_next(DLnode* p)
{
if (p == NULL) {
return;
}
DLnode* q = p->next; //找到p的后继结点
if (q == NULL) {
return;
}
p->next = q->next;
if (q->next != NULL) //q不是最后一个结点
{
q->next->prior = p;
}
free(q);
}
/*销毁一个双向链表*/
void DestotyDLinkList(DLinkList L)
{
//循环释放各个数据结点
while (L->next != NULL)
{
DeleteDLnode_next(L); //删除头结点的后继节点
free(L); //释放头结点
L = NULL;
}
}
/*双链表的遍历操作——前向遍历*/
while (p != NULL)
{
//对接点p做相应处理,并打印
p = p->prior;
}
/*双链表的遍历操作——后向遍历*/
while (p != NULL) {
//对结点p做相应处理,eg打印
p = p->next;
}
双向循环链表
#include<stdio.h>
#include<stdlib.h>
typedef struct Lnode {
int data; //数据域
struct Lnode* prior, * next; //前驱和后继指针
}DLnode, * DLinkList;
/*初始化空的循环双向链表*/
void InitDLinkList(DLinkList L)
{
L=(DLnode*)malloc(sizeof(DLnode));
if (L == NULL)
{
//提示空间不足,分配失败
return;
}
L->prior = L; //头结点的前驱&后继指针都指向头结点
L->next = L;
}
//判断循环双向链表是否为空
int IsEmpty(DLinkList L)
{
if (L->next == L)
{
return 1;
}
else return -1;
}
//判断p结点是否为循环双向链表的表尾结点
int IsTail(DLinkList L, DLnode* p) {
if (p->next == L)
{
return 1;
}
else return -1;
}
//双向循环链表的插入
void InsertNextDLnode(DLnode* p, DLnode* s)
{
s->next = p->next;
p->next->prior = s;
s->prior = p;
p->next = s;
}
//双向链表的删除操作
void DeleteDLnode(DLnode* p)
{
if (p == NULL) {
return;
}
DLnode* q = p->next; //找到p的后继结点
if (q == NULL) {
return;
}
p->next = q->next;
if (q->next != NULL) //q不是最后一个结点
{
q->next->prior = p;
}
free(q);
}