一、腐烂的橘子
1、题目描述: 在给定的 m x n 网格 grid 中,每个单元格可以有以下三个值之一:
值 0 代表空单元格;
值 1 代表新鲜橘子;
值 2 代表腐烂的橘子。
每分钟,腐烂的橘子 周围 4 个方向上相邻 的新鲜橘子都会腐烂。
返回 直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能,返回 -1
2、示例如下:
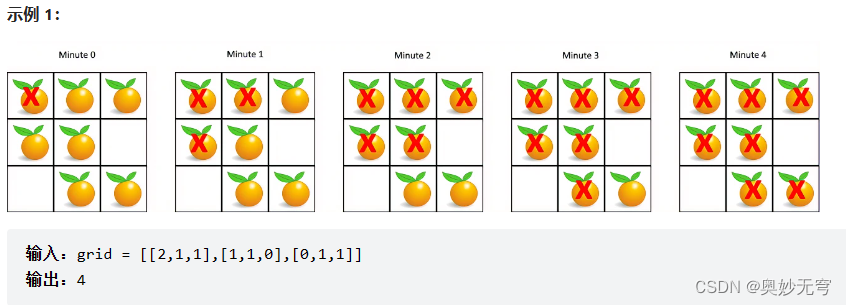
3、代码如下:
class Solution {
public int orangesRotting(int[][] grid) {
//边界,长和宽
int M=grid.length;
int N=grid[0].length;
Queue<int[]> queue=new LinkedList<>();
int count=0; //新鲜橘子的数量
for(int i=0;i<M;i++){
for(int j=0;j<N;j++){
if(grid[i][j]==1){
count++; //记录新鲜橘子
}else if(grid[i][j]==2){
queue.add(new int[]{i,j}); //腐烂的橘子也记录下来
}
}
}
int round=0; //时间、轮次
while(count>0&&!queue.isEmpty()){ //当没有新鲜橘子且队列中的腐烂橘子遍历完时退出循环
round++;
int n=queue.size(); //记录当前层级的腐烂橘子数量,因为每层都会更新队列
for(int i=0;i<n;i++){
int[] orange=queue.poll(); //将当前层最先放入的橘子拿出
int r=orange[0];
int c=orange[1];
if(r-1>=0&&grid[r-1][c]==1){ //更新四周橘子的状态
grid[r-1][c]=2;
count--;
queue.add(new int[]{r-1,c});
}
if(r+1<M&&grid[r+1][c]==1){
grid[r+1][c]=2;
count--;
queue.add(new int[]{r+1,c});
}
if(c-1>=0&&grid[r][c-1]==1){
grid[r][c-1]=2;
count--;
queue.add(new int[]{r,c-1});
}
if(c+1<N&&grid[r][c+1]==1){
grid[r][c+1]=2;
count--;
queue.add(new int[]{r,c+1});
}
}
}
if(count>0){ //若依然存在新鲜橘子,说明腐烂的橘子不可达
return -1;
}else{ //若不存在则输出轮次
return round;
}
}
}
二、查找单入口空闲区域
1、题目描述: 给定一个 m x n 的矩阵,由若干字符 ‘X’ 和 'O’构成,'X’表示该处已被占据,'O’表示该处空闲,请找到最大的单入口空闲区域。
解释:
空闲区域是由连通的’O’组成的区域,位于边界的’O’可以构成入口,单入口空闲区域即有且只有一个位于边界的’O’作为入口的由连通的’O’组成的区域。
如果两个元素在水平或垂直方向相邻,则称它们是“连通”的。
2、示例如下:

3、代码如下:
import java.util.*;
public class danRuKou {
public static int m;
public static int n;
public static String[][] strings;
public static int[] rukou=new int[2]; //入口坐标
public static int count=0; //入口个数
public static void main(String[] args){
Scanner sc=new Scanner(System.in);
m=sc.nextInt();
n=sc.nextInt();
strings=new String[m][n];
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
strings[i][j]=sc.next();
//System.out.println(strings[i][j]);
}
}
int max=0;
List<int[]> quyu=new ArrayList<>();
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
if(strings[i][j].equals("O")){ //从左上开始遍历寻找第一个为O的坐标
strings[i][j]="X";
List<int[]> zuobiao=new ArrayList<>(); //保存当前空闲区域的所有坐标
zuobiao.add(new int[]{i,j});
qiuquyu(i,j,zuobiao); //求当前空闲区域的所有坐标
if(count==1){ //如果入口只有一个则进行比较
if(max==zuobiao.size()){ //有大小相同的单入口空闲区域,则只需要大小,无需坐标
quyu.clear();
}else if(max<zuobiao.size()){ //若有更大的单入口空闲区域,则清除前面的那个,将当前的单入口空闲区域坐标放进去
quyu.clear();
quyu.add(new int[]{rukou[0],rukou[1],zuobiao.size()});
max=zuobiao.size();
}
}
count=0;
rukou=new int[2];
}
}
}
if(quyu.size()==1){ //如果单入口空闲区域只有1个,则直接输出
int[] res=quyu.get(0);
System.out.println(res[0]+" "+res[1]+" "+res[2]);
}else if(max!=0){ //如果最大区域的面积不止为0,则输出最大区域
System.out.println(max);
}else { //如果没找到,则输出NULL
System.out.println("NULL");
}
}
//得到单入口区域
public static void qiuquyu(int x,int y,List<int[]> list){
if(x==0||x==m-1||y==0||y==n-1){
count++;
rukou[0]=x;
rukou[1]=y;
}
if (x<m-1){
if(strings[x+1][y].equals("O")){ //因为是按顺序来,所以只需要向右或者向下遍历即可
strings[x+1][y]="X";
list.add(new int[]{x+1,y});
qiuquyu(x+1,y,list);
}
}
if (y<n-1){
if(strings[x][y+1].equals("O")){
strings[x][y+1]="X";
list.add(new int[]{x,y+1});
qiuquyu(x,y+1,list);
}
}
}
}
三、开心消消乐
1、题目描述: 给定一个N行M列的二维矩阵,矩阵中每个位置的数字取值为0或1。矩阵示例如:
1 1 0 0
0 0 0 1
0 0 1 1
1 1 1 1
现需要将矩阵中所有的1进行反转为0,规则如下:
1)当点击一个1时,该1变被反转为0,同时相邻的上、下、左、右,以及左上、左下、右上、右下8个方向的1(如果存在1)均会自动反转为0;
2)进一步地,一个位置上的1被反转为0时,与其相邻的8个方向的1(如果存在1)均会自动反转为0;
按照上述规则示例中的矩阵只最少需要点击2次后,所有值均为0。请问,给定一个矩阵,最少需要点击几次后,所有数字均为0?
2、示例如下:

3、代码如下:
import java.util.*;
public class kaiXingXiaoXiaoLe {
public static int[][] juzhen;
public static int N;
public static int M;
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
N=sc.nextInt();
M=sc.nextInt();
juzhen=new int[N][M];
for (int i=0;i<N;i++){ //保存二维数组
for (int j=0;j<M;j++){
juzhen[i][j]=sc.nextInt();
}
}
int res=0;
for (int i=0;i<N;i++){ //开始清除
for (int j=0;j<M;j++){
if (juzhen[i][j]==1){
clearHappy(i,j);
res++;
}
}
}
System.out.println(res);
}
//8个方向都清一遍
public static void clearHappy(int x,int y){
if (x>0){
if(juzhen[x-1][y]==1){ //正上
juzhen[x-1][y]=0;
clearHappy(x-1,y);
}
if(y>0){
if(juzhen[x-1][y-1]==1){ //左上
juzhen[x-1][y-1]=0;
clearHappy(x-1,y-1);
}
}
if(y<M-1){
if(juzhen[x-1][y+1]==1){ //右上
juzhen[x-1][y+1]=0;
clearHappy(x-1,y+1);
}
}
}
if(x<N-1){
if(juzhen[x+1][y]==1){ //正下
juzhen[x+1][y]=0;
clearHappy(x+1,y);
}
if(y>0){
if(juzhen[x+1][y-1]==1){ //左下
juzhen[x+1][y-1]=0;
clearHappy(x+1,y-1);
}
}
if(y<M-1){
if(juzhen[x+1][y+1]==1){ //右下
juzhen[x+1][y+1]=0;
clearHappy(x+1,y+1);
}
}
}
if(y>0){
if(juzhen[x][y-1]==1){ //正左
juzhen[x][y-1]=0;
clearHappy(x,y-1);
}
}
if(y<M-1){
if(juzhen[x][y+1]==1){ //正右
juzhen[x][y+1]=0;
clearHappy(x,y+1);
}
}
}
}