引言

上一节使用公式推导的方式介绍了狄利克雷过程中标量参数 $\alpha$ 的极端取值对于生成的随机测度 $\mathcal G^{(i)}$ 离散程度的影响。本节从随机测度的生成角度对标量参数 $\alpha$ 与离散程度的关系进行描述。

回顾：狄利克雷过程——定义

已知 $\mathcal G^{(i)}$ 服从狄利克雷过程 $\text{DP}(\alpha,\mathcal H)$ ：
$\mathcal G^{(i)} \sim \text{DP}(\alpha,\mathcal H)$

其中， $\mathcal G^{(i)}$ 被称作随机测度( $\text{Random Measure}$ )，它是从狄利克雷过程 $\text{DP}(\alpha,\mathcal H)$ 中生成的一个样本；并且它的本质是一个离散型概率分布。

假设该分布 $\mathcal G^{(i)}$ 是一个一维随机分布，并且其内部包含 $\mathcal K$ 个离散特征：
$\mathcal G^{(i)} = (g_1^{(i)},g_2^{(i)},\cdots,g_{\mathcal K}^{(i)})^T \quad \sum_{k=1}^{\mathcal K} g_k^{(i)} = 1$
其中 $g_k^{(i)}$ 表示 $\mathcal G^{(i)}$ 中的第 $k$ 个特征，它的权重信息。其他权重信息对应的示例结果表示如下：
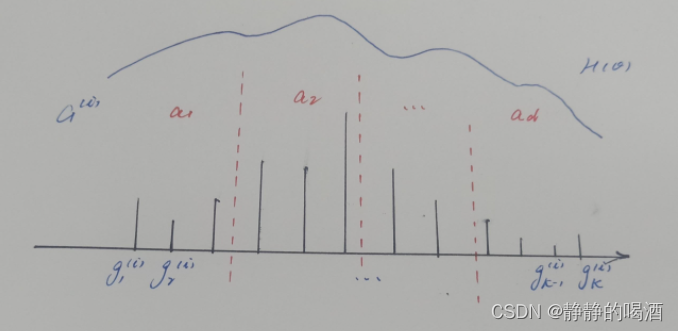
一维随机测度示例
其中，图像中竖线的长度就表示特征权重信息的大小。我们将 $\mathcal K$ 个权重结果划分成 $\mathcal D$ 个区域，每个区域中可能存在若干个权重结果：

其中 $a_d(d=1,2,\cdots,\mathcal D)$ 表示区域编号; $\mathcal G^{(i)}(a_d)$ 表示区域 $a_d$ 内存在的权重结果之和。
这仅是一个特征信息重组的部分，总量没有发生变化。
$\left\{\mathcal G^{(i)}(a_1),\mathcal G^{(i)}(a_2),\cdots,\mathcal G^{(i)}(a_{\mathcal D})\right\} \quad \begin{cases} \mathcal G^{(i)}(a_d) = \sum_{g_k^{(i)} \in a_d} g_k^{(i)} \\ \quad \\ \sum_{d=1}^{\mathcal D} \mathcal G^{(i)}(a_d) = 1 \end{cases}$

这意味 $\mathcal G^{(i)}(a_d)(d=1,2,\cdots,\mathcal D)$ 同样是随机变量。关于新的离散分布 $\left\{\mathcal G^{(i)}(a_1),\mathcal G^{(i)}(a_2),\cdots,\mathcal G^{(i)}(a_{\mathcal D})\right\}$ ，它需要服从的性质是狄利克雷分布：

并且‘狄利克雷分布’内部对应参数信息是 $\alpha \mathcal H(a_d)(d=1,2,\cdots,\mathcal D)$
可以比较 $\mathcal H(\theta^{(i)})$ 与 $\mathcal H(a_d)$ 的意义，它们均表示基本测度，只不过 $a_d$ 区域中可能包含若干个 $\theta$ .
$\left\{\mathcal G^{(i)}(a_1),\mathcal G^{(i)}(a_2),\cdots,\mathcal G^{(i)}(a_{\mathcal D})\right\} \sim \text{Dir} \left[\alpha \mathcal H(a_1),\alpha \mathcal H(a_2),\cdots,\alpha \mathcal H(a_{\mathcal D})\right]$

随机测度的生成过程

现在已经知道了狄利克雷过程的定义，那么随机测度 $\mathcal G^{(i)}$ 要如何生成呢？自然是采样( $\text{Sampling}$ )。在蒙特卡洛方法介绍中提到了关于从分布中生成的方式。如拒绝采样( $\text{Rejection Sampling}$ )：
$\mathcal M \cdot \mathcal Q(x) \geq \mathcal P(x)$
重要性采样( $\text{Importance Sampling}$ )等等：
$\mathbb E_{\mathcal P(x)} [f(x)] \approx \frac{1}{N} \sum_{i=1}^N \left[f(x^{(i)}) \cdot \frac{\mathcal P(x^{(i)})}{\mathcal Q(x^{(i)})}\right]$
但这些采样方式仅针对于单个样本。

经过上面的介绍， $\mathcal G^{(i)}$ 并不是一个简单样本，而是一个完整分布。在极大似然估计与最大后验概率估计中介绍过，概率分布是一个客观的存在，它可以源源不断地产生样本。

如何去采出一个存在无穷样本的分布？我们直接从样本的权重信息进行采样，构造一个过程。这个过程也被称作折棍子过程( $\text{Stick-breaking}$ )：

已知关于参数 $\theta = \{\theta^{(i)}\}_{i=1}^N$ 的基本测度 $\mathcal H(\theta)$ 。首先从 $\mathcal H(\theta)$ 中随机采样出一个样本 $\theta^{(i)}$ ：
$\theta^{(k)} \sim \mathcal H(\theta)$
下一步，我们需要采样它的权重信息：
- 在 $\theta^{(k)}$ 被确定后，它就已经是随机离散测度 $\mathcal G^{(i)}$ 中的一个随机变量了，按照理论来说，这种随机变量是无穷无尽的，因为我们从 $\mathcal H(\theta)$ 中源源不断的产生样本。
- 随着样本 $\theta^{(k)}$ 的增多, $\mathcal G^{(i)}$ 的离散程度越低，最终会成为连续分布。为了保证 $\mathcal G^{(i)}$ 是离散分布，关于 $\theta^{(k)}$ 权重的分配是至关重要的。
- 通过观察发现, $\theta^{(k)}$ 的生成仅与基本测度 $\mathcal H(\theta)$ 相关，和标量参数 $\alpha$ 无关。
假定 $\theta^{(k)}$ 对应的权重为 $\pi^{(k)}$ ，该值服从 $\text{Beta}$ 分布：
关于 $\text{Beta}$ 分布，该分布中的样本值域均为 $(0, 1]$ ,并且关于 $\text{Beta(a,b)}$ 分布的期望(该分布的位置)与参数 $a, b$ 之间的关系为: $\mathbb E[x] = \frac{a}{a + b}$ .
$\pi^{(k)} = \beta_1 \sim \text{Beta}(1,\alpha)$
此时， $\theta^{(k)}$ 对应权重 $\pi^{(k)}$ 已经采样完成。继续采集后续的样本。再次从 $\mathcal H(\theta)$ 中采出一个样本 $\theta^{(j)}$ ，继续计算它的权重信息：
- 和第一个样本 $\theta^{(k)}$ 不同的是，它需要从除去 $\pi^{(k)}$ 后的剩余权重中获取相应的权重.
- 很明显，就像‘折棍子’一样，如果将 $(0, 1]$ 视作完整的棍子，那么每次迭代过程中，每折掉一段，就将剩余的长度到下次迭代时，再进行折断。
  $\begin{cases} \theta^{(j)} \sim \mathcal H(\theta) \\ \beta_2 \sim \text{Beta}(1,\alpha) \\ \pi^{(j)} = (1 - \pi^{(k)}) \cdot \beta_2 \end{cases}$
以此类推，直到权重全部被分配出去，此时的概率分布就完成了，此时就生成了一个随机测度 $\mathcal G^{(i)}$ 。
从上述的过程可以发现，虽然都是从 $\text{Beta}(1,\alpha)$ 中随机结果，但是随着‘棍子’的长度缩短，对应的权值结果是‘递减’的。越往后迭代产生的权重，对于整个分布的影响越小。

从随机测度的生成过程观察标签参数 $\alpha$ 与随机测度离散程度之间的关系

关于从 $\text{Beta}(1,\alpha)$ 分布中产生的权值结果 $\beta$ ，它的期望表示如下：
$\mathbb E[x] = \frac{1}{1 + \alpha}$
而期望在 $\text{Beta}$ 分布表示 被采样概率最高的样本位置，实际它就是确定了 $\text{Beta}$ 分布的位置。

如果 $\alpha = 0$ 时，对应的期望结果 $\mathbb E[x] = 1$ ，这意味着第一次采样的时候就将所有的权重全部分配给第一个样本；剩余的样本没有任何权重；
相反，当 $\alpha = \infty$ 时，对应的期望结果 $\mathbb E[x] \to 0$ ，这意味着每一次采样仅能获取无限接近于 $0$ 的权重，也就是说，即便采集了无穷个样本，也无法将权重消耗完，那么此时的分布 $\mathcal G^{(i)}$ 就是基本测度 $\mathcal H$ 。