目录
一、搜索二叉树
1.1 搜索二叉树概念
二、模拟实现二叉搜索树
2.1 框架
2.2 构造函数
2.2.1 构造函数
2.2.2 拷贝构造
2.2.3 赋值拷贝
2.3 插入函数
2.3.1 insert()
2.3.2 RcInsert() 递归实现
2.4 删除结点函数
2.4.1 Erase()
2.4.2 RcErase()
2.5 中序遍历
2.6 查找函数find()
2.7 析构函数
2.8 测试函数
三、AVL算法实现平衡二叉搜索树
3.1 普通搜索二叉树的性能分析
3.2 AVL树概念与性质
3.3 AVL树结点的定义
3.4 AVL树结点插入
3.5 AVL树旋转算法保持树平衡
3.5.1 新节点插入较高左子树的左侧---左左:右单旋
3.5.2 新节点插入较高右子树的右侧---右右:左单旋
3.5.3 新节点插入较高左子树的右侧---左右:先左单旋再右单旋
3.5.4 新节点插入较高右子树的左侧---右左:先右单旋再左单旋
3.6 判断一个搜索二叉树是否为平衡
3.7 测试AVL树
一、搜索二叉树
1.1 搜索二叉树概念
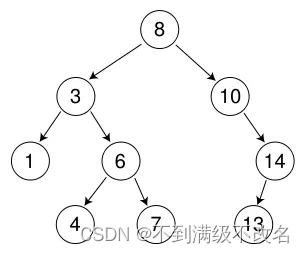
百度:
搜索二叉树或者是一棵空树,或者是具有下列性质的二叉树: 若它的左子树不空,则左子树上所有结点的值均小于它的根节点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值 。
二、模拟实现二叉搜索树
2.1 框架
namespace K
{
//结点类
template <class T>
class BSNode
{
public:
BSNode(const T& data = T())
:_data(data),
_left(nullptr),
_right(nullptr)
{}
public:
T _data;
BSNode<T>* _left;
BSNode<T>* _right;
};
//搜索二叉树
template<class T>
class BSTree
{
public:
typedef BSNode<T> Node;
BSTree();
BSTree(const BSTree<T>& t);
BSTree<T>& operator=(BSTree<T> tmp);
~BSTree();
bool insert(const T& x = T());
//中序遍历(从小到大)
void InOrder();
bool find(const T& x);
bool Erase(const T& x);
//recursive 递归实现
bool RcFind(const T& x);
bool RcInsert(const T& x);
bool RcErase(const T& x);
private:
Node* root;
};
}2.2 构造函数
2.2.1 构造函数
BSTree()
:root(nullptr)
{}2.2.2 拷贝构造
void copyTree(const Node* r)
{
if (r == nullptr)
return;
insert(r->_data);
copyTree(r->_left);
copyTree(r->_right);
}
BSTree(const BSTree<T>& t)
:root(nullptr)
{
copyTree(t.root);
}2.2.3 赋值拷贝
BSTree<T>& operator=(BSTree<T> tmp)
{
swap(root, tmp.root);
return *this;
}2.3 插入函数
2.3.1 insert()
bool insert(const T& x = T())
{
if (root == nullptr)
{
root = new Node(x);
return true;
}
//root!=nullprt
Node* cur = root;
Node* prev = nullptr;
while (cur)
{
prev = cur;
//比根大,往右子树走
if (x > cur->_data)
{
cur = cur->_right;
}
//比根小,往左子树走
else if (x < cur->_data)
{
cur = cur->_left;
}
//相等不符合规则,返回false
else
return false;
}
//链接(比根小,链左边,比根大链右边)
cur = new Node(x);
if (x > prev->_data) prev->_right = cur;
else prev->_left = cur;
return true;
}2.3.2 RcInsert() 递归实现
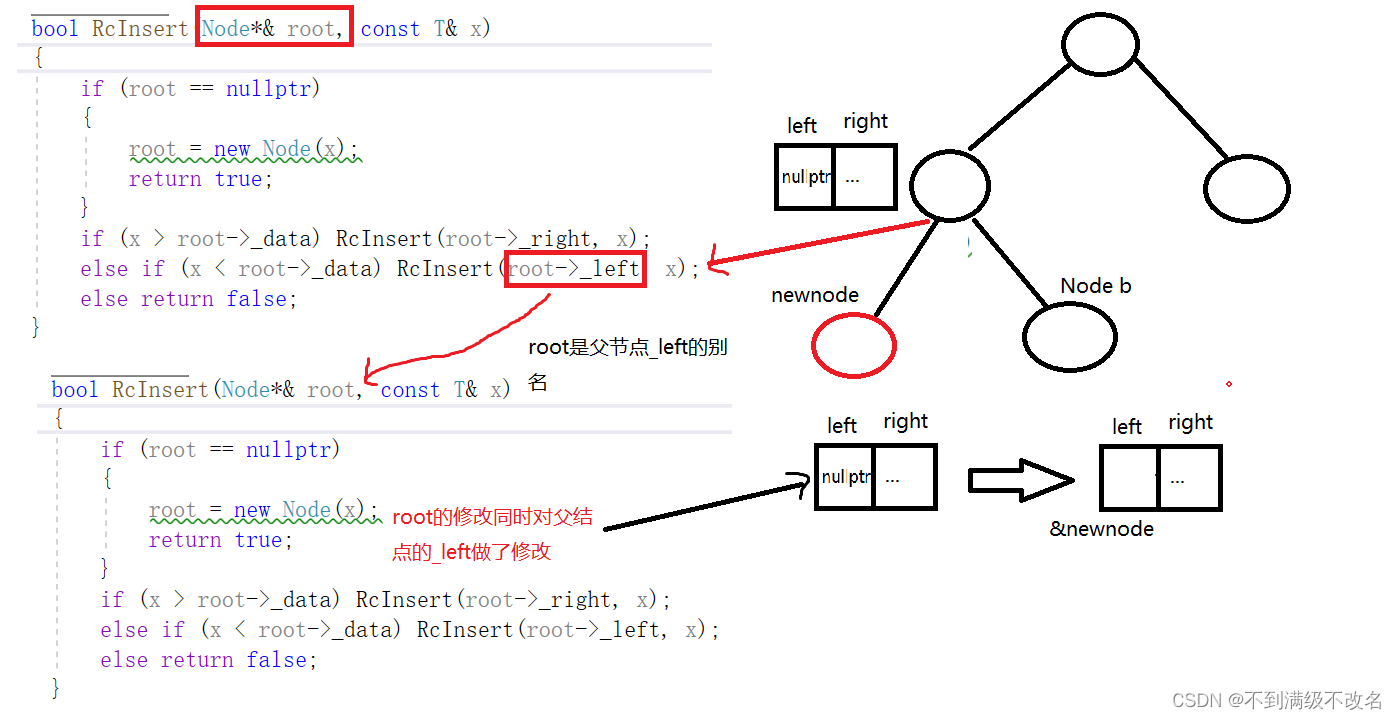
public:
bool RcInsert(const T& x)
{
return _RcInsert(root, x);//因为根的私有性,我们用间接调用的方式实现函数功能
}
private:
bool _RcInsert(Node*& root, const T& x)
{
if (root == nullptr)
{
root = new Node(x);
return true;
}
if (x > root->_data) _RcInsert(root->_right, x);
else if (x < root->_data) _RcInsert(root->_left, x);
else return false;
}2.4 删除结点函数


2.4.1 Erase()
bool Erase(const T& x)
{
if (root == nullptr)
return false;
Node* cur = root;
Node* prev = nullptr;
// 找到要删除的结点
while (cur)
{
if (x > cur->_data)
{
prev = cur;
cur = cur->_right;
}
else if (x < cur->_data)
{
prev = cur;
cur = cur->_left;
}
else break;
}
//情况c
if (cur->_left == nullptr)
{
if (prev == nullptr)
{
root = cur->_right;
}
else
{
if (cur->_data > prev->_data)
prev->_right = cur->_right;
else prev->_left = cur->_right;
}
delete cur;
}
//情况b
else if (cur->_right == nullptr)
{
if (prev == nullptr)
{
root = cur->_left;
}
else
{
if (cur->_data > prev->_data)
prev->_right = cur->_left;
else prev->_left = cur->_left;
}
delete cur;
}
//情况d
else
{
Node* minRight = cur->_right;
prev = cur;
while (minRight->_left)
{
prev = minRight;
minRight = minRight->_left;
}
cur->_data = minRight->_data;
//千万要记得先将minRight的右结点和其父节点链接在一起
if (minRight == prev->_left)
prev->_left = minRight->_right;
else prev->_right = minRight->_right;
delete minRight;
}
return true;
}2.4.2 RcErase()
public:
bool RcErase(const T& x)
{
return _RcErase(root, x);
}
private:
bool _RcErase(Node*& root, const T& x)
{
if (root == nullptr)
return false;
if (x > root->_data) _RcErase(root->_right, x);
else if (x < root->_data) _RcErase(root->_left, x);
else
{
Node* tmp = root;
if (root->_left == nullptr)
{
root = root->_right;
delete tmp;
}
else if (root->_right == nullptr)
{
Node* tmp = root;
root = root->_left;
delete tmp;
}
else
{
Node* minRight = root->_right;
while (minRight->_left)
{
minRight = minRight->_left;
}
root->_data = minRight->_data;
//递归删除minright
_RcErase(root->_right, root->_data);
}
}
return true;
}2.5 中序遍历
public:
void InOrder()
{
_InOrder(root);
cout << endl;
}
private:
void _InOrder(Node* root)
{
if (root == nullptr)
return;
_InOrder(root->_left);
cout << root->_data << ' ';
_InOrder(root->_right);
}2.6 查找函数find()
bool find(const T& x)
{
if (root == nullptr)
return false;
Node* cur = root;
while (cur)
{
if (x > cur->_data)
cur = cur->_right;
else if (x < cur->_data)
cur = cur->_left;
else return true;
}
return false;
}2.7 析构函数
public:
~BSTree()
{
Destroy(root);
}
private:
void Destroy(Node* root)
{
if (root == nullptr)
return;
Destroy(root->_left);
Destroy(root->_right);
delete root;
}2.8 测试函数
void TestBSTree1()
{
int arr[] = { 7,3,5,2,1,9,4,8,6 };
K::BSTree<int> tree;
for (auto e : arr)
{
tree.insert(e);
}
tree.InOrder();
for (int i = 1;i <= 9;i++)
{
tree.Erase(i);
tree.InOrder();
}
}
void TestBSTree2()
{
int arr[] = { 7,3,5,2,1,9,4,8,6 };
K::BSTree<int> tree1;
for (auto e : arr)
{
tree1.RcInsert(e);
}
tree1.InOrder();
K::BSTree<int> tree2;
tree2 = tree1;
tree2.InOrder();
}三、AVL算法实现平衡二叉搜索树
3.1 普通搜索二叉树的性能分析

最优情况下,二叉搜索树为完全二叉树(或者接近完全二叉树),其平均比较次数为:logN
最差情况下,二叉搜索树退化为单支树(或者类似单支),其平均比较次数为:O(N)
3.2 AVL树概念与性质
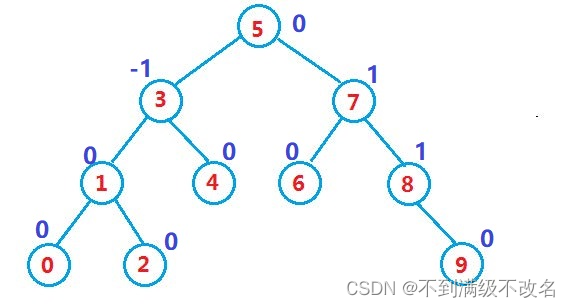
二叉搜索树虽可以缩短查找的效率,但如果数据有序或接近有序二叉搜索树将退化为单支树,查找元素相当于在顺序表中搜索元素,效率低下。
因此,两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明了一种解决上述问题的方法:当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整),即可降低树的高度,从而减少平均搜索长度。
性质:
1.它的左右子树都是AVL树
2.左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1) 高度差=右树高 - 左树高3.AVL树的查找效率为O(logN)
3.3 AVL树结点的定义
template <class T>
struct AVLTreeNode
{
public:
AVLTreeNode(const T& data)
:_data(data)
,_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_bf(0)
{}
AVLTreeNode<T>* _left;
AVLTreeNode<T>* _right;
AVLTreeNode<T>* _parent;
T _data;
int _bf;//树的平衡因子
};3.4 AVL树结点插入
bool insert(const T& data)
{
if (_root == nullptr)
{
_root = new Node(data);
return true;
}
//找到插入位置
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
parent = cur;
if (data > cur->_data)
cur = cur->_right;
else if (data < cur->_data)
cur = cur->_left;
else
return false;
}
//插入新节点并建立链接
cur = new Node(data);
cur->_parent = parent;
if (cur->_data > parent->_data)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
//判断平衡因子
while (parent)
{
if (cur == parent->_left)
{
parent->_bf--;
}
else
{
parent->_bf++;
}
if (parent->_bf == 0)
break;
else if (parent->_bf == -1 || parent->_bf == 1)
{
cur = parent;
parent = parent->_parent;
}
else if (parent->_bf == -2 || parent->_bf == 2)
{
//右高 右右
if (parent->_bf == 2 && cur->_bf == 1)
RotateL(parent);
//左高 左左
else if (parent->_bf == -2 && cur->_bf == -1)
RotateR(parent);
//右高 右左
else if (parent->_bf == 2 && cur->_bf == -1)
RotateRL(cur);
//左高 左右
else if (parent->_bf == -2 && cur->_bf == 1)
RotateLR(cur);
//任何其他情况都直接报错
else assert(false);
break;
}
else
{
assert(false);
}
}
return true;
}3.5 AVL树旋转算法保持树平衡
3.5.1 新节点插入较高左子树的左侧---左左:右单旋
情况一:左边高且插入结点在父节点左边!
以30结点为轴,将30的右结点与父节点链接,然后将60做30的右结点,这样就可以使树保持为平衡搜索树!

void RotateR(Node* parent)
{
Node* SubL = parent->_left;//父节点的左孩子
Node* SubLR = SubL->_right;//左孩子的右孩子
parent->_left = SubLR;//将左孩子的右孩子与父节点的左链接
if (SubLR) SubLR->_parent = parent;//右孩子不为空,则找父亲
//下面准备更新SubL为父节点,记录祖父节点
Node* gparent = parent->_parent;
//更新的节点是根节点,则直接改变root
if (parent == _root)
{
_root = SubL;
SubL->_parent = nullptr;
}
else {
//判断父节点与祖父节点的关系
if (parent == gparent->_left)
gparent->_left = SubL;
else gparent->_right = SubL;
//与祖父节点链接
SubL->_parent = parent->_parent;
}
//与原父节点链接,其链接在新父节点右
SubL->_right = parent;
parent->_parent = SubL;
//更新平衡因子
parent->_bf = SubL->_bf = 0;
}3.5.2 新节点插入较高右子树的右侧---右右:左单旋

情况二:右边高且插入结点在父节点的右边
以60为轴,将60的左结点与父节点30的右链接,将父节点30与60的左链接!
void RotateL(Node* parent)
{
Node* SubR = parent->_right;
Node* SubRL = SubR->_left;
parent->_right = SubRL;
if (SubRL) SubRL->_parent = parent;
Node* gparent = parent->_parent;
if (parent == _root)
{
_root = SubR;
SubR->_parent = nullptr;
}
else {
if (parent == gparent->_left)
gparent->_left = SubR;
else gparent->_right = SubR;
SubR->_parent = gparent;
}
SubR->_left = parent;
parent->_parent = SubR;
parent->_bf = SubR->_bf = 0;
}3.5.3 新节点插入较高左子树的右侧---左右:先左单旋再右单旋
先以60为轴进行左旋,然后以60为轴进行右旋

这里插入新节点后60节点的平衡因子对最后的的30,90平衡因子右影响!
如果60的平衡因子是-1,最后90的平衡因子就是1,30的平衡因子是0。
如果60的平衡因子是1,最后90的平衡因子就是0,30的平衡因子是-1。
如果60的平衡因子是0.最后30,90的平衡因子都是0。
void RotateLR(Node* parent) //parent --> 30节点
{
Node* SubR = parent->_right;
int bf = SubR->_bf; //记录插入新节点后的60的平衡因子
Node* gparent = parent->_parent; //gparent --> 90节点
RotateL(parent); //30以60为轴左旋
RotateR(gparent); //90以60为轴右旋
if (bf == 1)
{
SubR->_bf = 0;
parent->_bf = 0;
gparent->_bf = -1;
}
else if (bf == -1)
{
SubR->_bf = 0;
parent->_bf = 0;
gparent->_bf = 1;
}
else {
SubR->_bf = parent->_bf = gparent->_bf = 0;
}
}3.5.4 新节点插入较高右子树的左侧---右左:先右单旋再左单旋
先以60为轴进行右旋,然后以60为轴进行左旋!
同样我们30,90最后平衡因子的更新需要判断60的平衡因子!
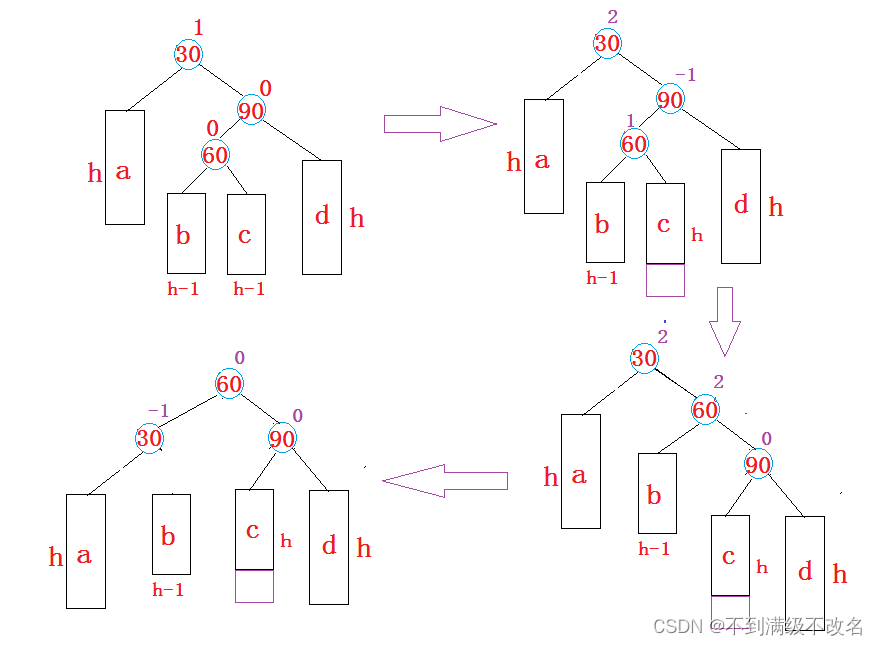
void RotateRL(Node* parent)
{
Node* SubL = parent->_left;
int bf = SubL->_bf;
Node* gparent = parent->_parent;
RotateR(parent);
RotateL(gparent);
if (bf == 1)
{
SubL->_bf = 0;
parent->_bf = -1;
gparent->_bf = 0;
}
else if (bf == -1)
{
SubL->_bf = 0;
parent->_bf = 0;
gparent->_bf = 1;
}
else {
SubL->_bf = parent->_bf = gparent->_bf = 0;
}
}3.6 判断一个搜索二叉树是否为平衡
//深层遍历,计算每个节点的高度
int TreeHeight(Node* root)
{
if (root == nullptr)
return 0;
int Left_height = TreeHeight(root->_left);
int Right_height = TreeHeight(root->_right);
//返回左右子树的最大高度+ 1(自己本身) ==此节点的高度
return Left_height > Right_height ? Left_height + 1 : Right_height + 1;
}
bool IsBalanceTree(Node* root)
{
if (root == nullptr)
return true;
int Left_height = TreeHeight(root->_left);
int Right_height = TreeHeight(root->_right);
//判断 1.此时高度下是否满足平衡 2.左子树是否满足 3.右子树是否满足
return abs(Left_height - Right_height) <= 1 && IsBalanceTree(root->_left) && IsBalanceTree(root->_right);
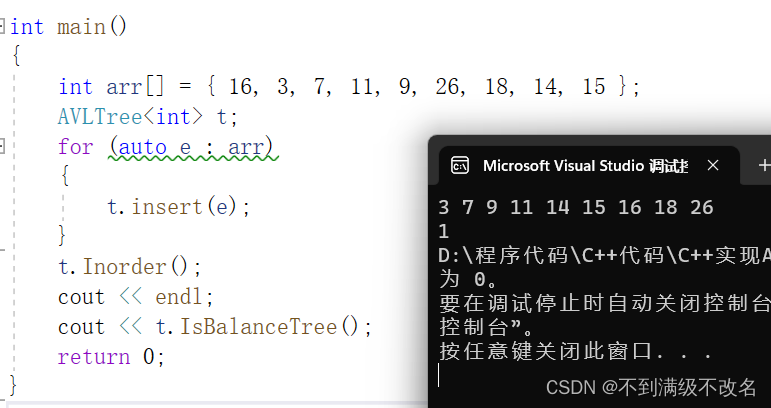
}3.7 测试AVL树