1378：最短路径(shopth)
时间限制: 1000 ms         内存限制: 65536 KB
【题目描述】
给出一个有向图G=(V, E)，和一个源点v0∈V，请写一个程序输出v0和图G中其它顶点的最短路径。只要所有的有向环权值和都是正的，我们就允许图的边有负值。顶点的标号从1到n（n为图G的顶点数）。
【输入】
第1行：一个正数n（2≤n≤80），表示图G的顶点总数。
第2行：一个整数，表示源点v0（v0∈V，v0可以是图G中任意一个顶点）。
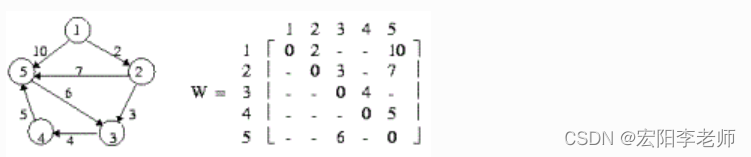
第3至第n+2行，用一个邻接矩阵W给出了这个图。
【输出】
共包含n-1行，按照顶点编号从小到大的顺序，每行输出源点v0到一个顶点的最短距离。每行的具体格式参照样例。
【输入样例】
5
1
0 2 - - 10
- 0 3 - 7
- - 0 4 -
- - - 0 5
- - 6 - 0
【输出样例】
(1 -> 2) = 2
(1 -> 3) = 5
(1 -> 4) = 9
(1 -> 5) = 9
【提示】
样例所对应的图如下:

//示例代码 floyd
#include <bits/stdc++.h>
using namespace std;
int f[85][85];
int n,v;
int main()
{
	memset(f,0x3f,sizeof(f));
	string s;
	cin>>n>>v;
	for(int i=1;i<=n;i++) f[i][i]=0;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++){
			cin>>s;
			if(s=="-") continue;
			else f[i][j]=atoi(s.c_str());
		}
	for(int k=1;k<=n;k++)
		for(int i=1;i<=n;i++)
			for(int j=1;j<=n;j++)
				f[i][j]=min(f[i][j],f[i][k]+f[k][j]);
	for(int i=1;i<=n;i++)
		if(i!=v) cout<<"("<<v<<" -> "<<i<<")"<<" = "<<f[v][i]<<endl;
	return 0;
}