给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。

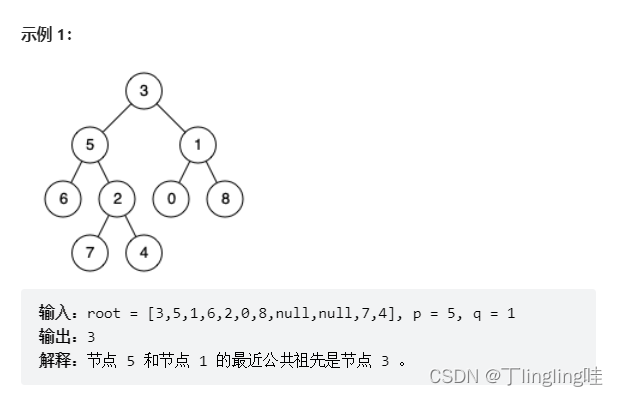
一开始我想的比较简单，我的思路是：
用两个list $pfather$和 $qfather$ 来记录寻找节点$p$和$q$、的路径，最后比对两条路径最早的公共节点
完成的代码如下：

class Solution(object):
    def dfs(self,root,father,son):
        Flag = False
        if not root:return False
        if root == son:
            father.append(root)
            return True
        if root.left:
            Flag = Flag or self.dfs(root.left,father,son)
        if root.right:
            Flag = Flag or self.dfs(root.right,father,son)
        if Flag:
            father.append(root)
            return Flag
    def lowestCommonAncestor(self, root, p, q):
        """
        :type root: TreeNode
        :type p: TreeNode
        :type q: TreeNode
        :rtype: TreeNode
        """
        pfather = []
        qfather = []
        self.dfs(root,pfather,p)
        self.dfs(root,qfather,q)
        res = root
        while(pfather and qfather and pfather[-1]==qfather[-1]):
            res = pfather.pop()
            qfather.pop()
        return res

• 针对$left$和$right$分支分别寻找$p$和$q$， 如果$left$和$right$都有返回节点，说明一条分支有$p$，一条分支有$q$，当前节点就是它们最近的公共祖先。
• 若$left$返回了节点，而$right$没有，说明最近的公共祖先肯定在$left$分支，不再考虑$right$。
• 若$right$返回了节点，而$left$没有，与上一情况同理。
• 针对$left$和$right$分支都没有返回节点，说明当前节点不可能是$p$和$q$的公共祖先，返回$None$。
  后来受到评论的题目启发，思路打开了，对深度搜索的情况进行如下分类：

综合以上情况返回代码如下：

class Solution(object):
    def lowestCommonAncestor(self, root, p, q):
        """
        :type root: TreeNode
        :type p: TreeNode
        :type q: TreeNode
        :rtype: TreeNode
        """
        if not root or root == p or root == q:
            return root
        left = self.lowestCommonAncestor(root.left, p, q)
        right = self.lowestCommonAncestor(root.right, p, q)
        if left and right:
            return root
        return left or right

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-tree