AcWing蓝桥杯辅导课：第二讲二分与前缀和

AcWing 789. 数的范围

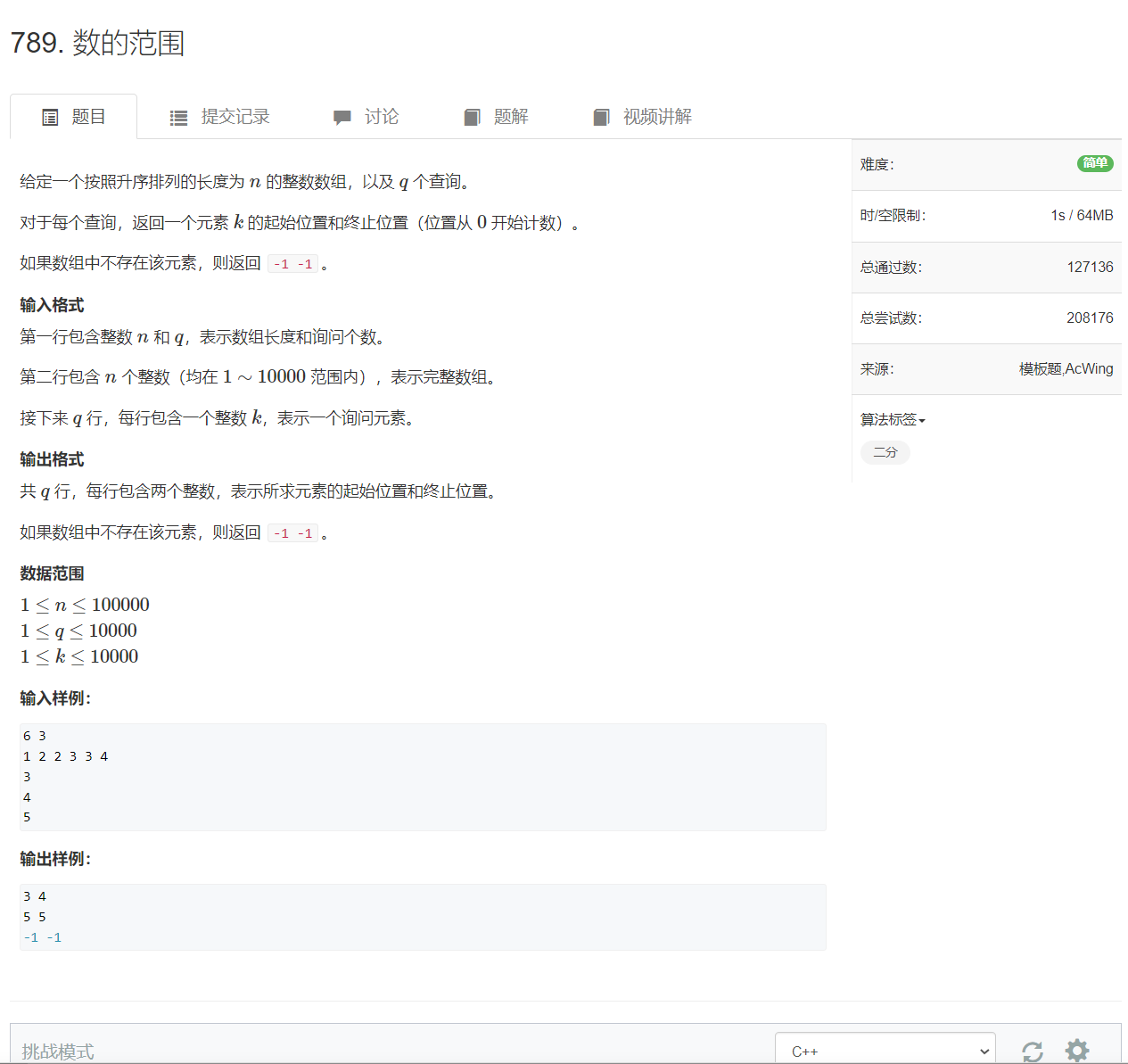
在这里插入图片描述
思路：

二分模板一共有两个，分别适用于不同情况。
算法思路：假设目标值在闭区间[l, r]中，每次将区间长度缩小一半，当l = r时，我们就找到了目标值。

版本1
当我们将区间[l, r]划分成[l, mid]和[mid + 1, r]时，其更新操作是r = mid或者l = mid + 1;，计算mid时不需要加1。

版本2
当我们将区间[l, r]划分成[l, mid - 1]和[mid, r]时，其更新操作是r = mid - 1或者l = mid;，此时为了防止死循环，计算mid时需要加1。

二分查找时，如果满足当前的 check() 函数，则继续二分。当查找数的左边界时，check() 函数为 a[mid] >= x，满足条件时，需要更新右边界，r = mid，否则更新左边界 l = mid + 1，此时将区间[l, r]划分成[l, mid]和[mid + 1, r]，用的是第一版本的二分， mid = l + r >> 1。

当查找数的右边界时，check() 函数为 a[mid] <= x，满足条件时，需要更新左边界，l = mid，否则更新右边界 r = mid - 1，此时将区间[l, r]划分成[l, mid - 1]和[mid, r]，用的是第二版本的二分，mid = l + r + 1 >> 1。

如果第一轮二分的结果，a[l] != x || a[r] != x，则不存在 x，此时输出 -1 - 1 即可。

代码：

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;

/**
 * @Description
 * @Author: PrinceHan
 * @CreateTime: 2023/2/25 8:05
 */
public class Main {
    static final int N = 100005;
    static int[] a = new int[N];
    static int n, q, k;

    public static void main(String[] args) throws IOException {
        BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
        PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
        String[] s = in.readLine().split(" ");
        n = Integer.parseInt(s[0]);
        q = Integer.parseInt(s[1]);

        String[] arr = in.readLine().split(" ");
        for (int i = 0; i < n; i++) a[i] = Integer.parseInt(arr[i]);

        while (q-- != 0) {
            int x = Integer.parseInt(in.readLine());
            int l = 0, r = n - 1;

            while (l < r) {
                int mid = l + r >> 1;
                if (a[mid] >= x) r = mid;
                else l = mid + 1;
            }

            if (a[l] != x) out.println("-1 -1");
            else {
                out.print(l + " ");
                l = 0;
                r = n - 1;

                while (l < r) {
                    int mid = l + r + 1 >> 1;
                    if (a[mid] <= x) l = mid;
                    else r = mid - 1;
                }

                out.print(r + "\n");
            }
        }
        out.flush();
    }
}

另外，使用 BufferedReader 与 PrintWriter 替换 Scanner 与 System.out.println()输入输出后，性能有了较大的飞跃。

在这里插入图片描述

AcWing 790. 数的三次方根

在这里插入图片描述
思路：

浮点数二分，最后的精度要求要比给定的要再精确两位。比如结果要求6位小数，则 eps = 1e-8。更新左右边界是将 mid 的值赋值给左右边界，当左右边界的差值小于精度 eps 时，就结束二分。

代码：

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;

/**
 * @Description
 * @Author: PrinceHan
 * @CreateTime: 2023/2/25 9:02
 */
public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
        PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
        double n = Double.parseDouble(in.readLine());
        double eps = 1e-8;
        double l = -10000, r = 10000;

        while (r - l > eps) {
            double mid = (l + r) / 2;
            if (mid * mid * mid >= n) r = mid;
            else l = mid;
        }

        out.printf("%.6f", l);
        out.flush();
    }
}

AcWing 795. 前缀和

在这里插入图片描述
思路：
前缀和以 $O (1)$ 的复杂度求出一段区间的和。

代码：

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;

/**
 * @Description
 * @Author: PrinceHan
 * @CreateTime: 2023/2/25 9:10
 */
public class Main {
    static final int N = 100005;
    static int n, m;
    static int[] a = new int[N], s = new int[N];

    public static void main(String[] args) throws IOException {
        BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
        PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));

        String[] nm = in.readLine().split(" ");
        n = Integer.parseInt(nm[0]);
        m = Integer.parseInt(nm[1]);

        String[] arr = in.readLine().split(" ");
        for (int i = 1; i <= n; i++) {
            a[i] = Integer.parseInt(arr[i - 1]);
            s[i] = a[i] + s[i - 1];
        }

        while (m-- != 0) {
            int l, r;
            String[] lr = in.readLine().split(" ");
            l = Integer.parseInt(lr[0]);
            r = Integer.parseInt(lr[1]);
            out.println(s[r] - s[l - 1]);
        }
        out.flush();
    }
}

AcWing 796. 子矩阵的和

在这里插入图片描述
代码：

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;

/**
 * @Description
 * @Author: PrinceHan
 * @CreateTime: 2023/2/25 9:22
 */
public class Main {
    static final int N = 1005;
    static int n, m, q;
    static int[][] s = new int[N][N];
    
    public static void main(String[] args) throws IOException {

        BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
        PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));

        String[] nm = in.readLine().split(" ");
        n = Integer.parseInt(nm[0]);
        m = Integer.parseInt(nm[1]);
        q = Integer.parseInt(nm[2]);
        
        for (int i = 1; i <= n; i++) {
            String[] sub = in.readLine().split(" ");
            for (int j = 1; j <= m; j++) {
                s[i][j] = Integer.parseInt(sub[j - 1]);
            }
        }
        
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
            }
        }
        
        while (q-- != 0) {
            int x1, y1, x2, y2;
            String[] idx = in.readLine().split(" ");
            x1 = Integer.parseInt(idx[0]);
            y1 = Integer.parseInt(idx[1]);
            x2 = Integer.parseInt(idx[2]);
            y2 = Integer.parseInt(idx[3]);
            out.println(s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]);
        }
        out.flush();
    }
}

AcWing 730. 机器人跳跃问题

在这里插入图片描述
思路：

设初始能量值为 $E$ ，下一座建筑高度为 $H (i)$ ，分为两种情况：

$E < H (i)$ ，失去 $H (i) - E$ 的能量值，当前能量值为 $2 E^{'} - H (i)$
$E > H (i)$ ，得到 $E - H (i)$ 的能量值，当前能量值为 $2 E^{'} - H (i)$

则只需寻找满足所有的 $2 E^{'} - H (i)$ 的 $E$ 的最小值，因此可以用到二分。

代码：

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;

/**
 * @Description
 * @Author: PrinceHan
 * @CreateTime: 2023/2/27 8:20
 */
public class Main {

    static final int N = 100005;
    static int[] h = new int[N];
    static int n;

    public static void main(String[] args) throws IOException {

        BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
        PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
        String[] nk = in.readLine().split(" ");
        n = Integer.parseInt(nk[0]);

        String[] hs = in.readLine().split(" ");
        for (int i = 1; i <= n; i++) h[i] = Integer.parseInt(hs[i - 1]);

        int l = 1, r = 100001;

        while (l < r) {
            int mid = (l + r) / 2;
            // 2E' - h > 0
            if (check(mid)) r = mid;
            else l = mid + 1;
        }

        out.println(r);
        out.flush();
    }

    public static boolean check(int mid) {
        for (int i = 1; i <= n; i++) {
            mid = mid * 2 - h[i];
            if (mid < 0) return false;
            // 防止溢出
            if (mid > N) return true;
        }
        return true;
    }
}

AcWing 1221. 四平方和

在这里插入图片描述
思路：

答案按字典序排列，可以得到 $a, b, c, d$ 均小于 $\sqrt n$ ，因此可以先枚举 $c, d$ ，并记录字典序最小的 $c * c + d * d$ 的组合。接着从小到大枚举 $a, b$ ，判断 $n - a * a - b * b$ 是否在 $c * c + d * d$ 的组合，如果有，就是字典序最小的解，输出即可。

代码：

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.util.Arrays;

/**
 * @Description
 * @Author: PrinceHan
 * @CreateTime: 2023/2/25 9:59
 */
public class Main {
    static final int N = 5000010;
    static int[] C = new int[N], D = new int[N];
    static int n;
    public static void main(String[] args) throws IOException {
        BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
        PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
        String[] nk = in.readLine().split(" ");
        n = Integer.parseInt(nk[0]);
        Arrays.fill(C, -1);

        for (int c = 0; c * c <= n / 2; c++) {
            for (int d = c; c * c + d * d <= n; d++) {
                int s = c * c + d * d;
                if (C[s] == -1) {
                    C[s] = c;
                    D[s] = d;
                }
            }
        }

        for (int a = 0; a * a <= n / 2; a++) {
            for (int b = a; a * a + b * b <= n; b++) {
                int sum = n - a * a - b * b;
                if (C[sum] != -1) {
                    out.printf("%d %d %d %d", a, b, C[sum], D[sum]);
                    out.flush();
                    return ;
                }
            }
        }
    }
}

AcWing 1227. 分巧克力

在这里插入图片描述
思路：

二分枚举边长的最大值，如果当前边长满足条件，更新左边界 l = mid，否则更新右边界 r = mid - 1

代码：

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;

/**
 * @Description
 * @Author: PrinceHan
 * @CreateTime: 2023/2/25 10:14
 */
public class Main {
    static final int N = 100005;
    static int[] h = new int[N], w = new int[N];

    public static void main(String[] args) throws IOException {
        BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
        PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));

        String[] nk = in.readLine().split(" ");
        int n = Integer.parseInt(nk[0]);
        int k = Integer.parseInt(nk[1]);
        int sq = 0;

        for (int i = 0; i < n; i++) {
            String[] s = in.readLine().split(" ");
            h[i] = Integer.parseInt(s[0]);
            w[i] = Integer.parseInt(s[1]);
        }

        int ans = 0;

        int l = 1, r = 100001;

        while (l < r) {
            long num = 0;
            int mid = l + r + 1>> 1;
            for (int i = 0; i < n; i++) {
                num += (long)h[i] / mid * (w[i] / mid);
            }
            if (num >= k) {
                l = mid;
            }
            else r = mid - 1;
        }

        out.println(l);
        out.flush();
    }
}

AcWing 99. 激光炸弹

在这里插入图片描述
思路：

典型的子矩阵的和的问题，首先对输入的 $R$ 的范围进行限制， $R = min (R, 5001)$ ，接着初始化子矩阵的和。接着枚举在 $R \times R$ 的范围内，价值的最大值。

代码：

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;

/**
 * @Description
 * @Author: PrinceHan
 * @CreateTime: 2023/2/25 11:29
 */
public class Main {
    static final int N = 5002;
    static int[][] s = new int[N][N];
    public static void main(String[] args) throws IOException {
        BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
        PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
        String[] nr = in.readLine().split(" ");
        int n = Integer.parseInt(nr[0]), r = Integer.parseInt(nr[1]);
        r = Math.min(5001, r);

        for (int i = 1; i <= n; i++) {
            String[] t = in.readLine().split(" ");
            int x = Integer.parseInt(t[0]), y = Integer.parseInt(t[1]), w = Integer.parseInt(t[2]);
            s[x + 1][y + 1] += w;
        }

        for (int i = 1; i <= 5001; i++) {
            for (int j = 1; j <= 5001; j++) {
                s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
            }
        }

        int max = 0;

        for (int i = r; i < N; i++) {
            for (int j = r; j < N; j++) {
                max = Math.max(s[i][j] - s[i - r][j] - s[i][j - r] + s[i - r][j - r], max);
            }
        }
        out.println(max);
        out.flush();
    }
}

AcWing 1230. K倍区间

在这里插入图片描述
思路：

暴力做即使加上前缀和的优化也需要 $O(N^2)$ 的时间复杂度，在本题的规模下要超时，因此需要独辟蹊径。

容易想到，如果两个数模 $n$ 同余，那么这两个数的差值是 $n$ 的倍数。所以可以记录前缀和模 $k$ 的余数，计算余数相同的前缀和的个数，任选两个前缀和的差值即为 $k$ 的倍数，这样只用 $O (N)$ 的时间复杂度就可以计算出 $K$ 倍区间的数目。

代码：

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;

/**
 * @Description
 * @Author: PrinceHan
 * @CreateTime: 2023/2/25 11:04
 */
public class Main {
    static final int N = 100005;
    static int[] s = new int[N];
    static int[] mod = new int[N];
    static long ans;
    static int n, k;
    public static void main(String[] args) throws IOException {
        BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
        PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
        String[] nk = in.readLine().split(" ");
        n = Integer.parseInt(nk[0]);
        k = Integer.parseInt(nk[1]);

		// 余数为0先赋值为1，当区间和为前缀和时，需要用到
        mod[0] = 1;
        for (int i = 1; i <= n; i++) {
            s[i] = Integer.parseInt(in.readLine().split(" ")[0]);
            s[i] += s[i - 1];
            s[i] %= k;
            mod[s[i]]++;
        }

        for (int i = 0; i <= k - 1; i++) {
            ans += (long) mod[i] * (mod[i] - 1) / 2;
        }
        out.println(ans);
        out.flush();
    }
}