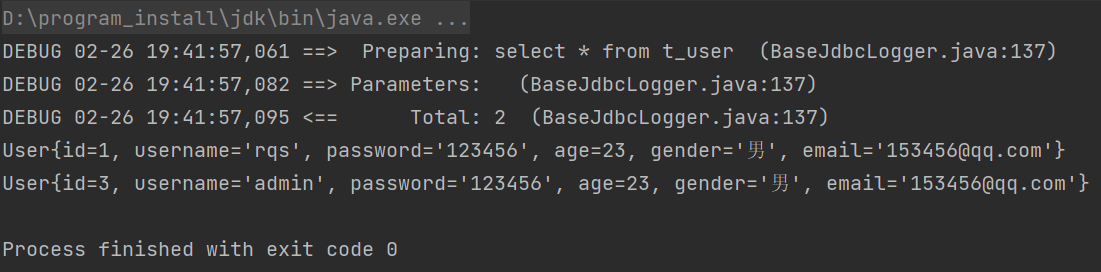
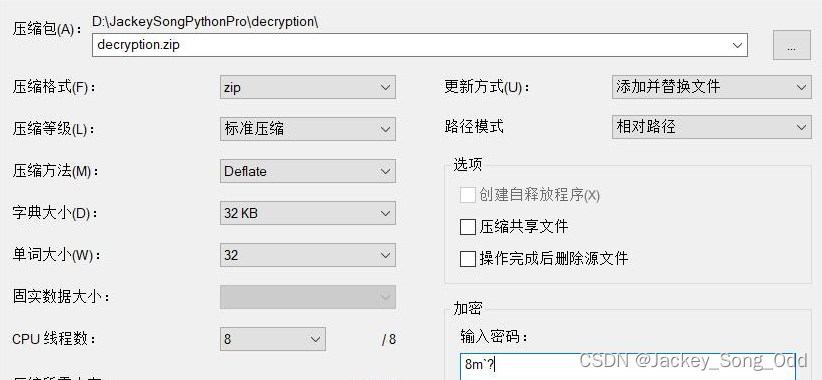
如果你有压缩包的密码忘记了，并且压缩包的加密算法采用的是ZipCrypto，并且压缩参数如下图所示：

那么你就可以使用本文中的方法进行破解。

压缩包的加密，是根据输入的密码进行运算加密，输入不同的密码，加密后的结果就是不同的二进制流。所以在进行解密的时候，不同的密码会解密出不同的结果，但是只有一种结果是你想要的正确的结果。

假设组成密码的字符总共有 a 个，密码是1 ~ n位，那么可以组合出 S 种不同的密码，一个字符占一个字节，所有密码的所有字符加在一起总共有 Q 个字节。下面分别给出 S 和 Q 的计算公式：
$$S=a^1+a^2+a^3+a^4+......+a^n\text{\hspace{1em}(1)}$$
$$aS=a^2+a^3+a^4+......+a^n+a^{n+1}\text{\hspace{1em}(2)}$$
(1)式减去(2)式得：
$$(1-a)S=a^1-a^{n+1}$$
最后可以化简得到：
$$S=\frac{a(1-a^n)}{1-a}.$$

$$Q=1\cdot a^1+2\cdot a^2+3\cdot a^3+......+n\cdot a^n\text{\hspace{1em}(3)}$$
$$aQ=1\cdot a^2+2\cdot a^3+3\cdot a^4+......+(n-1)\cdot a^n+n\cdot a^{n+1}\text{\hspace{1em}(4)}$$
(3)式减去(4)式得：
$$(1-a)Q=a^1+a^2+a^3+a^4+......+a^n-n\cdot a^{n+1}$$
化简得：
$$Q=\frac{a(1-a^n)}{(1-a{)}^2}+\frac{n\cdot a^{n+1}}{a-1}.$$

一开始，我的思路是先写一个程序，这个程序把所有的密码组合出来，写入一个文件，然后再写一个程序，这个程序负责把写入的密码读取出来，再逐个暴力破解。但是后来发现这种思路存在几个问题，如果密码的组合可能性太多的时候，那么存取所有密码的这个文件将会达到几十个G（甚至更大）。压缩包的密码位数可以是1 ~ 127位的（超过127位的密码也有）。以最大位数127位为例，假如不知道密码是多少位，那么可以组合出：
$$94^1+94^2+94^3+......+94^{126}+94^{127}$$
种不同的密码组合。使用上面的式子计算一下，就可以知道总共有：39073499766929905093170936199210360403225359398866973176589007276420630179610064715271048101086598784117989282816367722389837036292113256007435625512903036280893835514194448335273218252856958007222866912360893842268293858285256762926406241457713184768 种不同的密码。

如果将所有的密码组合写入文件，不算回车换行符号，那么这个文件将会占 4961914325241313777553199490046598363526519239925145287832966868945419472665422521762910503472996114196429684959005740369797942759811562831081763117671397554605682022967601468185686939482979425062618339967434564286481867349313821628002924237784812093440 个字节。

并且，如果正确密码是最后一个，那么将要循环到最后一个密码才能破解成功，这样将会很耗费时间。所以，我采用了随机密码暴力破解。

下面是代码：

import zipfile

import os

import numpy as np



pwdCharset = ['`', '~', '!', '@', '#', '$', '%', '^', '&', '*', '(', ')', '-', '_', '=', '+', '[', ']', '{', '}', ';', ':', "'", '"', '\\', '|', ',', '<', '.', '>', '/', '?', 'a', 'A', 'b', 'B', 'c', 'C', 'd', 'D', 'e', 'E', 'f', 'F', 'g', 'G', 'h', 'H', 'i', 'I', 'j', 'J', 'k', 'K', 'l', 'L', 'm', 'M', 'n', 'N', 'o', 'O', 'p', 'P', 'q', 'Q', 'r', 'R', 's', 'S', 't', 'T', 'u', 'U', 'v', 'V', 'w', 'W', 'x', 'X', 'y', 'Y', 'z', 'Z', '0', '1', '2', '3', '4', '5', '6', '7', '8', '9']
# 94\

CharsetInput = []


def gPwd(chST, lgth, rgth):
    while True:
        pl = int(np.random.random() * 100)
        if pl >= lgth and pl <= rgth:
            break

    pwd = ""

    chStLen = len(chST)

    for i in range(0, pl):
        while True:
            idx = int(np.random.random() * 100)
            if idx >= 0 and idx < chStLen:
                break
        pwd += chST[idx]

    return pwd


def dcryp(fileName, lLen, rLen, chST):
    fp = zipfile.ZipFile(fileName)

    count = 0

    while True:
        pwd = gPwd(chST, lLen, rLen)
        count += 1
        try:
            for file in fp.namelist():
                fp.extract(file, pwd=pwd.encode())
                os.rename(file, file.encode('cp437').decode('gbk'))
            print("%d Success! The password is %s" % (count, pwd))
            break
        except:
            print("%d %s no" % (count, pwd))


if __name__ == "__main__":
    fileName = input("请输入要破解的压缩包文件名:")
    choose = input("按1选择暴力破解。\n按2选择指定条件破解\n")

    if "1" == choose:
        leftLen = int(input("确定密码的长度范围:\n请输入密码的最小长度:"))
        rightLen = int(input("请输入密码的最大长度:"))
        dcryp(fileName, leftLen, rightLen, pwdCharset)
    elif "2" == choose:
        charSt = input("请输入密码中可能包含的字符:\n")
        for i in charSt:
            CharsetInput.append(i)
        leftLen = int(input("确定密码的长度范围:\n请输入密码的最小长度:"))
        rightLen = int(input("请输入密码的最大长度:"))
        dcryp(fileName, leftLen, rightLen, CharsetInput)
    else:
        print("无效输入！")

下面是测试：

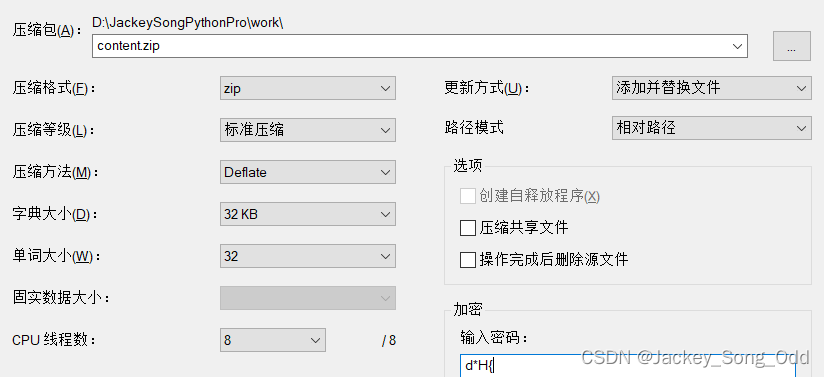
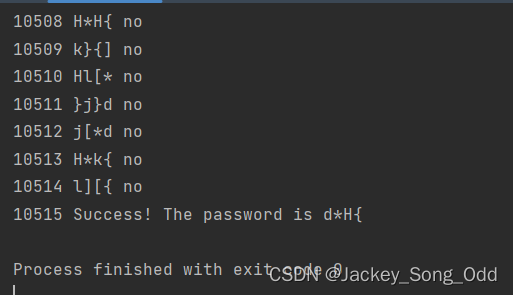
这里选用的是4位的定长密码，尝试了10515次，用了不到10秒钟的到结果。

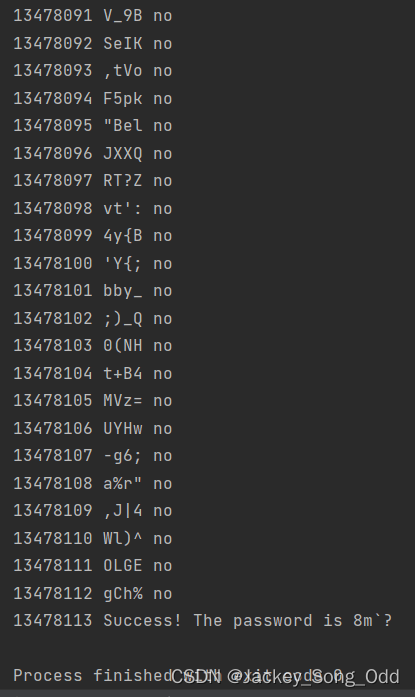
4位定长密码，如果不指定字符集，用所有可能的字符集暴力随机破解，总共有78074896种不同的密码组合，一共尝试了13478113次，将会用大概20多分钟的时间。

密码越长，且可能的字符越多，则破解的时间越长。

针对长而复杂的密码，如果加密的内容很重要，一定要破解出来的话，可以采用分布式破解，即一台主机通过网络将破解内容分发给一个计算机集群，集群中的每一台主机同时运行多个破解进程，并定期向控制主机发送心跳信号，反馈破解信息，这样可以大大缩短破解时间。