文章目录
一、二分查找习题练习
1、1 数的范围
1、1、1 题目描述
1、1、2 题解关键思路与解答
1、2 机器人跳跃问题
1、2、1 题目描述
1、2、2 题解关键思路与解答
1、3 四平方和
1、3、1 题目描述
1、3、2 题解关键思路与解答
二、前缀和习题练习
2、1 前缀和
2、1、1 题目描述
2、1、2 题解关键思路与解答
2、2 子矩阵的和
2、2、1 题目描述
2、2、2 题解关键思路与解答
三、总结
标题:蓝桥杯——二分与前缀和习题练习
作者:@Ggggggtm
寄语:与其忙着诉苦,不如低头赶路,奋路前行,终将遇到一番好风景
又来更新了。二分与前缀和是蓝桥杯比较常考的内容,所以我们要多加练习这方面的习题。二分与前缀和的难度相对来说不算大,我们应该掌握其关键要点。
一、二分查找习题练习
1、1 数的范围
1、1、1 题目描述
题目来源:模板题,AcWing
题目难度:简单
题目描述:
给定一个按照升序排列的长度为 n 的整数数组,以及 q 个查询。
对于每个查询,返回一个元素 k 的起始位置和终止位置(位置从 0 开始计数)。
如果数组中不存在该元素,则返回
-1。输入格式:
第一行包含整数 n 和 q,表示数组长度和询问个数。
第二行包含 n 个整数(均在 1∼10000 范围内),表示完整数组。
接下来 q 行,每行包含一个整数 k,表示一个询问元素。
输出格式:
共 q 行,每行包含两个整数,表示所求元素的起始位置和终止位置。
如果数组中不存在该元素,则返回
-1。数据范围:
1≤n≤100000
1≤q≤10000
1≤k≤10000输入样例:
6 3 1 2 2 3 3 4 3 4 5输出样例:
3 4 5 5 -1 -1
1、1、2 题解关键思路与解答
简单总结上述题目,就是让我们找出要求相同的数的左右区间。也就是我们需要找出要求的数的左边界与右边界。因为题目中描述的是有序的,所以我们在这里用二分就可以很容易找到题目所要求的左右边界。我们直接看代码:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int n,m;
const int N=100010;
int arr[N];
int main()
{
cin>>n>>m;
for(int i=0;i<n;i++)
scanf("%d",&arr[i]);
while(m--)
{
int k;
scanf("%d",&k);
int l=0,r=n-1;
while(l<r)
{
int mid=l+r>>1;
if(arr[mid]>=k)
r=mid;
else
l=mid+1;
}
if(arr[l]==k)
{
cout<<l<<' ';
r=n-1;
while(l<r)
{
int mid=l+r+1>>1;
if(arr[mid]<=k)
l=mid;
else
r=mid-1;
}
cout<<l<<endl;
}
else
{
cout<<"-1 -1"<<endl;
}
}
return 0;
}
1、2 机器人跳跃问题
1、2、1 题目描述
题目来源:今日头条2019笔试题
题目难度:简单
题目描述:
机器人正在玩一个古老的基于 DOS 的游戏。
游戏中有 N+1 座建筑——从 0 到 N 编号,从左到右排列。
编号为 0 的建筑高度为 0 个单位,编号为 i 的建筑高度为 H(i)个单位。
起初,机器人在编号为 0 的建筑处。
每一步,它跳到下一个(右边)建筑。
假设机器人在第 k 个建筑,且它现在的能量值是 E,下一步它将跳到第 k+1个建筑。
如果 H(k+1)>E,那么机器人就失去 H(k+1)−E的能量值,否则它将得到 E−H(k+1)的能量值。
游戏目标是到达第 N 个建筑,在这个过程中能量值不能为负数个单位。
现在的问题是机器人至少以多少能量值开始游戏,才可以保证成功完成游戏?
输入格式:
第一行输入整数 N。
第二行是 N 个空格分隔的整数,H(1),H(2),…,H(N) 代表建筑物的高度。
输出格式:
输出一个整数,表示所需的最少单位的初始能量值上取整后的结果。
数据范围:
1≤N,H(i)≤10e5
输入样例1:
5 3 4 3 2 4输出样例1:
4输入样例2:
3 4 4 4输出样例2:
4输入样例3:
3 1 6 4输出样例3:
3
1、2、2 题解关键思路与解答
这个题我们可以用二分加枚举来计算,时间复杂度为O(n*logn),最大数据为1e5,也是可以通过的。具体就是,我们可以二分能量,然后通过能量再去枚举看是否可以通过。这里需要注意的是要整形溢出的问题。
#include<iostream>
#include<cstdio>
using namespace std;
int n;
const int N=100010;
int a[N];
bool jump(int e)
{
for (int i = 0; i < n; i ++ )
{
//e = e * 2 - a[i];
//if (e < 0) return false;
if(a[i]>e)
e-=(a[i]-e);
else
e+=(e-a[i]);
if (e >= 1e5)
return true;
if(e<0)
return false;
}
return true;
}
int main()
{
scanf("%d",&n);
for(int i=0;i<n;i++)
{
scanf("%d",&a[i]);
}
int min=0,max=100010;
while(min<max)
{
int mid=min+max>>1;
if(jump(mid))
max=mid;
else
min=mid+1;
}
cout<<min<<endl;
return 0;
}1、3 四平方和
1、3、1 题目描述
题目来源:第七届蓝桥杯省赛C++A/B组,第七届蓝桥杯省赛JAVAB/C组
题目难度:中等
题目描述:
四平方和定理,又称为拉格朗日定理:
每个正整数都可以表示为至多 4 个正整数的平方和。
如果把 0 包括进去,就正好可以表示为 4 个数的平方和。
比如:
对于一个给定的正整数,可能存在多种平方和的表示法。
要求你对 4 个数排序:
0≤a≤b≤c≤d,并对所有的可能表示法按 a,b,c,d为联合主键升序排列,最后输出第一个表示法。
输入格式:
输入一个正整数 N。
输出格式:
输出4个非负整数,按从小到大排序,中间用空格分开。
数据范围
0<N<5∗1e6。
输入样例:
5输出样例:
0 0 1 2
1、3、2 题解关键思路与解答
由于题目给出的数据范围较大,所以我们在这里不能用暴力四层for循环来求解。我们可以先求出c和d两数的平方和,再把这两个数的平方和存起来并且排序。再去求a和b的平方和,通过二分去找已经算好的c和d的平方和,看是否满足条件。那我们如何保证0≤a≤b≤c≤d呢?我们再求和的时候是从大到小的,一旦找到解就返回即可。我们结合代码一起理解一下:
#include <cstring>
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
const int N = 2500010;
struct Sum
{
int s, c, d;
bool operator< (const Sum &t)const
{
if (s != t.s) return s < t.s;
if (c != t.c) return c < t.c;
return d < t.d;
}
}sum[N];
int n, m;
int main()
{
cin >> n;
for (int c = 0; c * c <= n; c ++ )
for (int d = c; c * c + d * d <= n; d ++ )
sum[m ++ ] = {c * c + d * d, c, d};
sort(sum, sum + m);
for (int a = 0; a * a <= n; a ++ )
for (int b = a; a * a + b * b <= n; b ++ )
{
int t = n - a * a - b * b;
int l = 0, r = m - 1;
while (l < r)
{
int mid = l + r >> 1;
if (sum[mid].s >= t) r = mid;
else l = mid + 1;
}
if (sum[l].s == t)
{
printf("%d %d %d %d\n", a, b, sum[l].c, sum[l].d);
return 0;
}
}
return 0;
}
二、前缀和习题练习
2、1 前缀和
2、1、1 题目描述
题目来源:《算法竞赛进阶指南》
题目难度:简单
题目描述:
输入一个长度为 n 的整数序列。
接下来再输入 m 个询问,每个询问输入一对 l,r。
对于每个询问,输出原序列中从第 l 个数到第 r 个数的和。
输入格式:
第一行包含两个整数 n 和 m。
第二行包含 n 个整数,表示整数数列。
接下来 m 行,每行包含两个整数 l 和 r,表示一个询问的区间范围。
输出格式:
共 m 行,每行输出一个询问的结果。
数据范围:
1≤l≤r≤n,
1≤n,m≤100000,
−1000≤数列中元素的值≤1000输入样例:
5 3 2 1 3 6 4 1 2 1 3 2 4输出样例:
3 6 10
2、1、2 题解关键思路与解答
题目要求是求一段区间的和。数组的元素个数和询问次数的数据范围为0到1e5,暴力循环求解是不行。这里我们可以用到前缀和,使的求一段区间的和的值从O (N)的时间复杂度优化到了O(1)。我们直接看代码:
#include<iostream>
#include<cstdio>
using namespace std;
const int N=100010;
int n,m;
int a[N],s[N];
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
s[i]=s[i-1]+a[i];
}
while(m--)
{
int l,r;
scanf("%d%d",&l,&r);
printf("%d\n",s[r]-s[l-1]);
}
return 0;
}2、2 子矩阵的和
2、2、1 题目描述
题目来源:《算法竞赛进阶指南》
题目难度:简单
题目描述:
输入一个 n 行 m 列的整数矩阵,再输入 q 个询问,每个询问包含四个整数 x1,y1,x2,y2,表示一个子矩阵的左上角坐标和右下角坐标。
对于每个询问输出子矩阵中所有数的和。
输入格式:
第一行包含三个整数 n,m,q。
接下来 n 行,每行包含 m 个整数,表示整数矩阵。
接下来 q 行,每行包含四个整数 x1,y1,x2,y2,表示一组询问。
输出格式:
共 q 行,每行输出一个询问的结果。
数据范围:
1≤n,m≤1000,
1≤q≤200000,
1≤x1≤x2≤n,
1≤y1≤y2≤m
−1000≤矩阵内元素的值≤1000输入样例:
3 4 3 1 7 2 4 3 6 2 8 2 1 2 3 1 1 2 2 2 1 3 4 1 3 3 4输出样例:
17 27 21
2、2、2 题解关键思路与解答
该题的题录与前缀和思路大致相同,只不过这道题求的前缀和变成了二位的前缀和。建议画图,利用容斥原理,仔细分析一下即可。相对还是较为简单的。
#include<iostream>
#include<cstdio>
using namespace std;
const int N=1010;
int a[N][N],s[N][N];
int n,m,q;
int main()
{
cin>>n>>m>>q;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
scanf("%d",&a[i][j]);
s[i][j]=s[i][j-1]+s[i-1][j]-s[i-1][j-1]+a[i][j];
}
while(q--)
{
int x1,x2,y1,y2;
scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
printf("%d\n",s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1]);
}
return 0;
}三、总结
通过上面的习题练习,我们发现二分和前缀和的思想很简单。同时,我们也要掌握上面的二分和前缀和的思路和方法。在很多情况下,会给我们带来很大的便利。
二分和前缀和的练习就到这里,希望以上内容对你有所帮助。

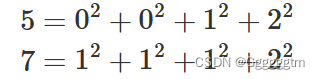


![[黑马程序员SSM框架教程] Spring-22 注解开发依赖注入](https://img-blog.csdnimg.cn/0e2553317e88456aa4510a3deabb7b2e.png)