浮点表示法
把一个数字的有效数字和数的范围在计算机的一个存储单元中分别予以表示。这种精度分别表示的方法,相当于数的小数点位置随比例因子的不同而在一定范围内可以浮点,所以称为浮点表示法。
在计算机中一个任意二进制数N可以写成
N = 2^e.M
其中M称为浮点数的尾数,是一个纯小数。e是比例因子的指数,称为浮点数的指数,是一个整数。
M:决定精度
E:数的大小
Es | Em-1 ··· E1 E0 | Ms | Mn-1 ··· M1M0 |
阶符(阶码符号) | 阶码 | 数符 | 尾数 |
浮点数规格化
浮点数的表示
1.11 X 2^0 = 0.111 X 2^1 = 11.1 X 2^-1
规范化的目的
保持浮点数表示的唯一性
保留更多地有效数字,提高运算的精度
规范化要求
1/R<=|尾数|<1; R为基数,如2,即大于等于1/2小于1
规范化处理
尾数向左移n位(小数点右移),同时阶码减n;
尾数向右移n位(小数点左移),同时阶码加n。
注意:这里说的是数值左右移动,而不是小数点,记住“左减右加”
尾数用原码表示
尾数数值最高位为1,0.1xxxx...
尾数用补码表示
尾数数值位和尾数符号位相反
正 | 0.1xxx | 正数三码合一 |
负 | 1.0xxx | 负数而言,补码从形式上看不好看化为原码,补补得原,补码的补码为原码,然后看大小 |
浮点数的数据表示范围
N = M · 2^e
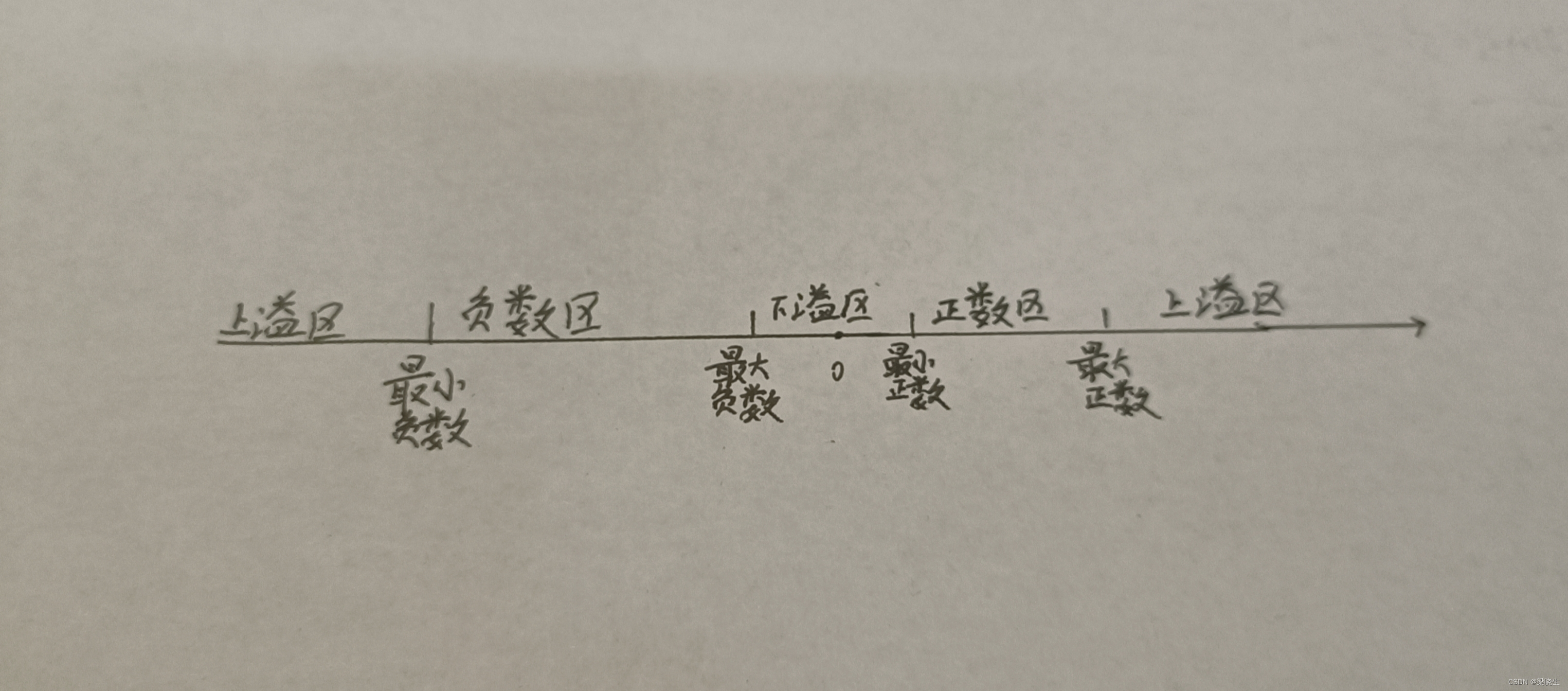
尾数 | 负的最小值 | 负的最大值 | 正的最小值 | 正的最大值 |
阶码 | 正的最大值 | 负的最小值 | 负的最小值 | 正的最大值 |
浮点数的溢出:阶码溢出(运算时候)
上溢:阶码大于所有表示的最大值;无穷
下溢:阶码小于所有表示的最小值;0
机器0:尾数为0,或阶码小于所能表示的最小值
32位浮点数的IEEE754标准表示
数符S | 阶码E | 尾数M |
第一个数符位取值0/1,第二个位置是8位阶码包含阶符,第三个是32位尾数:数值
数符S:表示浮点数的符号,占1位,0——正数、1——负数
尾数M:23位,原码纯小数表示,小数点在尾数域的最前面;
由于原码表示的要求,最高数值位始终为1,因为此标准中隐藏最高数值位(1),尾数的实际值位1.M;
尾数M最高值为1,好处:精度增加了,这里的1.M的1是数值
阶码E:8位,采用偏移值的移码表示,真值加127;
移1237码,即E = e+127,E的8位二进制数即为移127码的编码;
一个规格化的32位浮点数x的真值表示为
x = (-1)^S X (1.M) X 2^(E-127) e = E-127