一、等价类的作用

二、等价类的分类

三、等价类的方法

四、等价类的原则

五、按照测试用例的完整性划分等价类

六、等价类步骤

七、案例

一、等价类的作用

为穷举测试设计测试点。

穷举：列出所有的可能情况，对其一一判断。

测试点：要验证的点。比如测试登录界面：用户名为空、用户名错误、密码为空、密码错误等等。

我们不可能实现穷举测试，等价类划分法是把程序所有可能的输入数据，进行分类（有效和无效等价类），然后从分类中选取具有代表性的数据来设计测试用例。

二、等价类的分类

有效等价类：合理的、有意义的输入数据构成的集合；

无效等价类：不合理的、没有意义的输入数据构成的集合；

三、等价类的方法

按区间划分。

按数值划分。

按数值集合划分。

按限制条件或规划划分。

按处理方式划分。

四、等价类的原则

①在输入条件规定的取值范围或值的个数的情况下，可以确定一个有效等价类和两个无效等价类。

例如：有这样一个需求，用户名的长度为 [1,100]；

那么，一个有效等价类可以是：1≤x≤100；

两个无效等价类可以是：>1、<100；

知识扩展

看到这里有些人可能会疑惑，我的有效等价类不是在 1~100 之间吗，那我为什么不这样描述：>= 1并且 <= 100，而是描述为：1≤x≤100；这两种描述方式都可以使用，都是正确的描述方法。

还有一个问题，需求中是直接写 [1,100] 的，没有明确标明是 >= 1 并且 <= 100，还是 > 1 并且 < 100，那我为什么觉得他是 >= 1 并且 <= 100 呢?这里就要补充另一个知识点了；

不等式的小括号和中括号的含义

小括号和中括号在不等式里面表示一个取值范围，小括号是开区间，为不包含；中括号是闭区间，为包含。

比如：(1,100)，表示不等式的解集是 >1 并且 < 100（不包含1和100）。

也可以表示为：1＜x＜100；

比如 [1,100] ，表示不等式的解集是 >=1 并且 <= 100（包含1和100）。

也可以表示为：1 ≤ x ≤ 100。

所以我之前这样描述：1≤x≤100，就是 >=1 并且 <= 100 的意思。

注：

1.在不等式里第一个数字为大于，最后一位数字为小于；

2.我们知道怎么打出“<”，知道怎么打出"="，那怎么把他们两个组合起来，打出“≤”呢❓❓❓最简单的就是在输入的时候上直接写中文“小于等于”；

“≥”也是同理。

我说这个的原因是想让你们看到 1 ≤ x ≤ 100 这种描述的时候不会

，知道他表示的是什么意思就好，本来就理解的话就更好啦啦~

②在规定了输入数据的一组值中（假定有n个值），并且程序要对每个输入值分别处理的情况下，可以确定n个有效等价类和一个无效等价类。

例如：考试的时候单选题只能在A、B、C、D四个选项中选择；

那么，n个有效等价类可以是：A、B、C、D；

一个无效等价类可以是：不在A、B、C、D之内的选项；

③在规定输入数据必须遵守的规则的情况下，可以确定一个有效等价类和若干个无效等价类。

例如：密码由 1~8 位的数字+字母组成；

那么，一个有效等价类可以是：1≤x≤8位的数字+字母组成的密码；

若干个无效等价类可以是：空（也就是<1）、>8、1<x<8位的纯数字、1<x<8位纯字母、1<x<8位非数字+非字母（小数、中文、特殊符号）、空格；

④在输入条件规定了输入值的集合或规定了“必须如何”的条件下，可以确定一个有效等价类和一个无效等价类。

例如：输入三个正整数代表每边的长度，构成等边三角形；

那么，一个有效等价类可以是：三条边都相等的；

一个无效等价类可以是：三条边不相等的；

⑤在确定已划分的等价类中各元素在程序处理中的方式不同的情况下，则应将该等价类进一步地划分为更小的等价类。

例如：密码不可以含有空格；

那么，先划分大的有效和无效等价类，有效：不含有空格；无效：含有空格；

然后还可以对无效等价类进行进一步的划分：前面含空格、后面含空格、中间含空格；

五、按照测试用例的完整性划分等价类

可以分为：弱一般等价类、弱健壮等价类、强一般等价类、强健壮等价类。

弱一般等价类：

遵循单缺陷原则，要求用例覆盖每个变量的一个值，取有效值。

弱健壮等价类：

在弱一般等价类的基础上，加上无效值；“健壮”的意思就是程序要有容错能力，输入了无效值也能正确识别出来；对于有效输入，取每个有效变量的一个值；对于无效输入，取一个无效值，其余的都是有效值。

强一般等价类：

遵循多缺陷原则，取每个变量每个值的迪卡尔乘积，也就是所有变量和所有值的组合情况；比如，

X有 2 个等价类，Y有 3 个等价类，那他的迪卡尔乘积就是：2*3=6，最终用例的数量就是 6。

强健壮等价类：

在强一般等价类的基础上，加上无效值（不仅取单个无效值，也要取多个无效值）。

六、等价类步骤

1、划分有效和无效等价类表，并设定编号；

2、根据等价类表编写测试用例。

等价类表的建立

1）在分析需求规格说明的基础上划分等价类，列出等价类表，为每一个等价类规定一个唯一的编号。

2）将程序可能的输入数据分成若干个子集，从每个子集中选取一个有代表性的数据作为测试用例。等价类是某个输入域的子集，在该子集中的每个输入数据的作用都是等效的。

3）设计新的测试用例，使其尽可能多地覆盖未覆盖的有效等价类，按照这一步骤重复进行，直到所有的有效等价类都被覆盖为止。

4）设计新的测试用例，使其仅覆盖一个尚未被覆盖的无效等价类，按照这一步骤重复进行，直到所有的无效等价类都被覆盖为止。

七、案例

需求1：密码为 8-10 位数字字母组合。

等价表的格式：输入条件、输出条件（有就写）、有效等价类、有效等价类编号、无效等价类、无效等价类编号。

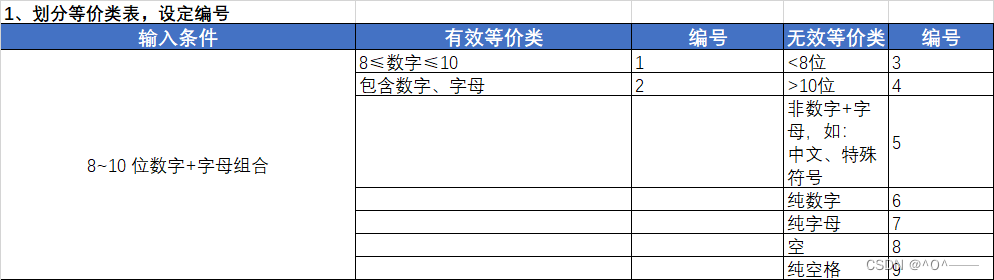
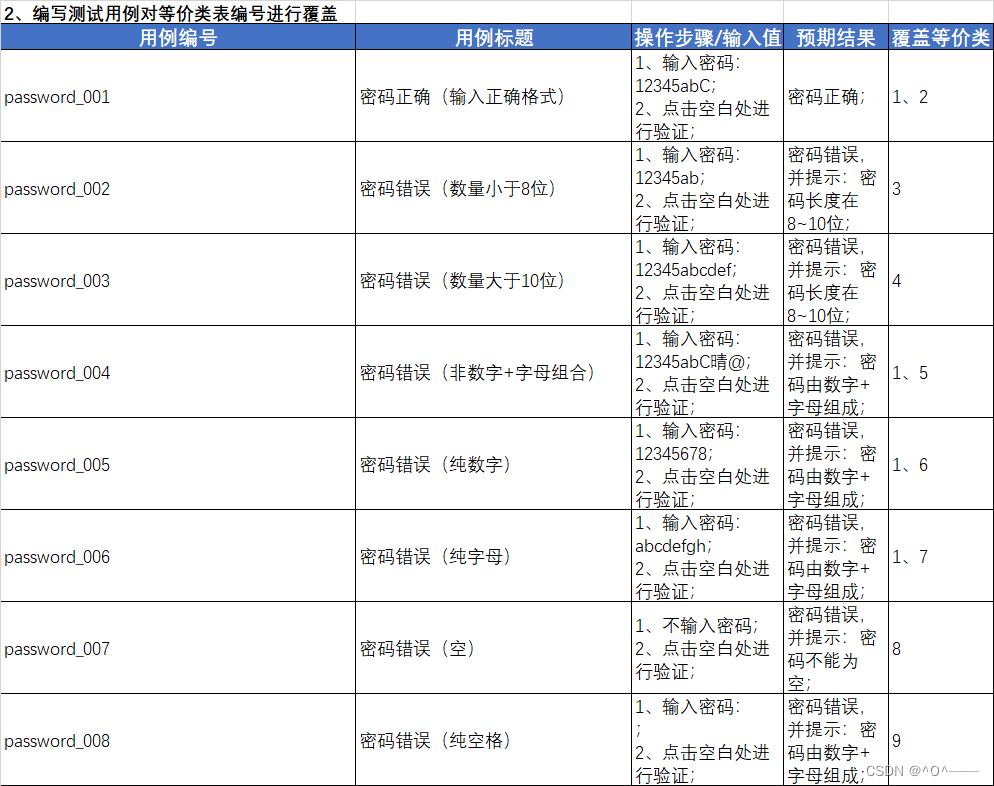注：为了节省时间，大致写了下，在企业里面写测试用例不单单只有这几要素。

需求2：输入三个正整数作为边长，判断这三条边能否构成三角形，若能，所构成的三角形是等边、等腰还是一般三角形，请用等价类划分法设计测试用例（面试题，真实碰到过！！！）。

假设

a代表第一条边的长度；

b代表为第二条边的长度；

c代表为第三条边的长度；

🤡一些解释

一般三角形：

任意两边之和大于第三边,任意两边之差小于第三边（一般情况下，只要将最短的两条边相加，将最长的边和最短的边相减即可得出是否能构成一般三角形）；

任意两边之和大于第三边，也就是：

1、a+b>c；

2、a+c>b；

3、b+c>a；

任意两边之差小于第三边，也就是：

1、a-b<c；

2、a-c<b；

3、b-c<a；

等腰三角形：

如果有两个边的长相等,则为等腰三角形；

也就是：

1、a=b!=c；

2、a=c!=b；

3、b=c!=a；

等边三角形：

如果三个边的长都相等,则为等边三角形；

也就是：

a=b=c；

什么是正整数？

除了“0”以外的整数。