C/C++每日一练(20230226)

news2024/9/25 1:17:55

目录

 

17. 电话号码的字母组合

37. 解数独

51. N 皇后

52. N皇后 II

89. 格雷编码

90. 子集 II

17. 电话号码的字母组合

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

示例 1：

输入：digits = "23"
输出：["ad","ae","af","bd","be","bf","cd","ce","cf"]

示例 2：

输入：digits = ""
输出：[]

示例 3：

输入：digits = "2"
输出：["a","b","c"]

提示：

  • 0 <= digits.length <= 4
  • digits[i] 是范围 ['2', '9'] 的一个数字。
#include <bits/stdc++.h>
using namespace std;

class Solution
{
public:
    vector<string> result;
    vector<string> letterCombinations(string digits)
    {
        string temp;
        if (digits.length() == 0)
            return result;
        getAns(digits, 0, temp, result);
        return result;
    }
    void getAns(string digits, int start, string temp, vector<string> &result)
    {
        if (temp.size() == digits.length())
            result.push_back(temp);
        else
        {
            vector<char> let = getLet(digits[start]);
            for (int i = 0; i < let.size(); i++)
            {
                temp.append(1, let[i]);
                getAns(digits, start + 1, temp, result);
                temp.pop_back();
            }
        }
    }
    vector<char> getLet(char i)
    {
        vector<char> let;
        if (i == '2')
        {
            let.push_back('a');
            let.push_back('b');
            let.push_back('c');
        }
        else if (i == '3')
        {
            let.push_back('d');
            let.push_back('e');
            let.push_back('f');
        }
        else if (i == '4')
        {
            let.push_back('g');
            let.push_back('h');
            let.push_back('i');
        }
        else if (i == '5')
        {
            let.push_back('j');
            let.push_back('k');
            let.push_back('l');
        }
        else if (i == '6')
        {
            let.push_back('m');
            let.push_back('n');
            let.push_back('o');
        }
        else if (i == '7')
        {
            let.push_back('p');
            let.push_back('q');
            let.push_back('r');
            let.push_back('s');
        }
        else if (i == '8')
        {
            let.push_back('t');
            let.push_back('u');
            let.push_back('v');
        }
        else if (i == '9')
        {
            let.push_back('w');
            let.push_back('x');
            let.push_back('y');
            let.push_back('z');
        }
        return let;
    }
};

int main()
{
	Solution s1;
	string digits = "23";
	for (auto comb : s1.letterCombinations(digits))
		cout << comb << " ";
	cout <<endl;

	Solution s2;
	digits = "";
	for (auto comb : s2.letterCombinations(digits))
		cout << comb << " ";
	cout <<endl;
	
	Solution s3;
	digits = "2";
	for (auto comb : s3.letterCombinations(digits))
		cout << comb << " ";

	return 0;
} 

#include <bits/stdc++.h>
using namespace std;

class Solution
{
public:
    unordered_map<char, string> map = {{'2', "abc"}, {'3', "def"}, {'4', "ghi"}, {'5', "jkl"}, {'6', "mno"}, {'7', "pqrs"}, {'8', "tuv"}, {'9', "wxyz"}};
    vector<string> res;
    void backtrack(string &s, int index, string cur)
    {
        if (index == s.size())
        {
            res.push_back(cur);
            return;
        }
        for (int i = 0; i < map[s[index]].size(); ++i)
            backtrack(s, index + 1, cur + map[s[index]][i]);
    }
    vector<string> letterCombinations(string digits)
    {
        if (digits.size() == 0)
            return res;
        string cur;
        backtrack(digits, 0, cur);
        return res;
    }
};

int main()
{
	Solution s1;
	string digits = "23";
	for (auto comb : s1.letterCombinations(digits))
		cout << comb << " ";
	cout <<endl;

	Solution s2;
	digits = "";
	for (auto comb : s2.letterCombinations(digits))
		cout << comb << " ";
	cout <<endl;
	
	Solution s3;
	digits = "2";
	for (auto comb : s3.letterCombinations(digits))
		cout << comb << " ";

	return 0;
} 

#include <bits/stdc++.h>
using namespace std;

class Solution
{
public:
    vector<string> letterCombinations(string digits)
    {
        if (digits.size() == 0)
            return {};
        map<char, string> a;
        a.insert(map<char, string>::value_type('2', "abc"));
        a.insert(map<char, string>::value_type('3', "def"));
        a.insert(map<char, string>::value_type('4', "ghi"));
        a.insert(map<char, string>::value_type('5', "jkl"));
        a.insert(map<char, string>::value_type('6', "mno"));
        a.insert(map<char, string>::value_type('7', "pqrs"));
        a.insert(map<char, string>::value_type('8', "tuv"));
        a.insert(map<char, string>::value_type('9', "wxyz"));
        int count = 1;
        for (int i = 0; i < digits.size(); i++)
        {
            count *= a[digits[i]].size();
        }
        vector<string> res(count);
        count = 1;
        for (int i = 0; i < digits.size(); i++)
        {
            int index = 0;
            vector<string> temp(res.begin(), res.begin() + count);
            for (int k = 0; k < count; k++)
            {
                for (auto c : a[digits[i]])
                {
                    res[index] = temp[k] + c;
                    index++;
                }
            }
            count *= a[digits[i]].size();
        }
        return res;
    }
};

int main()
{
	Solution s1;
	string digits = "23";
	for (auto comb : s1.letterCombinations(digits))
		cout << comb << " ";
	cout <<endl;

	Solution s2;
	digits = "";
	for (auto comb : s2.letterCombinations(digits))
		cout << comb << " ";
	cout <<endl;
	
	Solution s3;
	digits = "2";
	for (auto comb : s3.letterCombinations(digits))
		cout << comb << " ";

	return 0;
}

37. 解数独

编写一个程序，通过填充空格来解决数独问题。

数独的解法需 遵循如下规则：

  1. 数字 1-9 在每一行只能出现一次。
  2. 数字 1-9 在每一列只能出现一次。
  3. 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。（请参考示例图）

数独部分空格内已填入了数字，空白格用 '.' 表示。

示例：

输入：

board = 
    [["5","3",".",".","7",".",".",".","."],
    ["6",".",".","1","9","5",".",".","."],
    [".","9","8",".",".",".",".","6","."],
    ["8",".",".",".","6",".",".",".","3"],
    ["4",".",".","8",".","3",".",".","1"],
    ["7",".",".",".","2",".",".",".","6"],
    [".","6",".",".",".",".","2","8","."],
    [".",".",".","4","1","9",".",".","5"],
    [".",".",".",".","8",".",".","7","9"]]


输出：

    [["5","3","4","6","7","8","9","1","2"],
    ["6","7","2","1","9","5","3","4","8"],
    ["1","9","8","3","4","2","5","6","7"],
    ["8","5","9","7","6","1","4","2","3"],
    ["4","2","6","8","5","3","7","9","1"],
    ["7","1","3","9","2","4","8","5","6"],
    ["9","6","1","5","3","7","2","8","4"],
    ["2","8","7","4","1","9","6","3","5"],
    ["3","4","5","2","8","6","1","7","9"]]


解释：输入的数独如上图所示，唯一有效的解决方案如下所示：

 提示：

  • board.length == 9
  • board[i].length == 9
  • board[i][j] 是一位数字或者 '.'
  • 题目数据 保证 输入数独仅有一个解

#include <bits/stdc++.h>
using namespace std;

class Solution
{
public:
    void solveSudoku(vector<vector<char>> &board)
    {

        Dfs(board, 0);
    }

private:
    bool flag = false;
    void Dfs(vector<vector<char>> &board, int n)
    {

        if (n > 0 && n <= 81)
            if (!JudgeIsNoWant(board, n - 1))
                return;

        if (n >= 81)
        {
            flag = true;
            return;
        }

        int x = n / 9;
        int y = n % 9;

        if (board[x][y] != '.')
            Dfs(board, n + 1);
        else
        {

            for (int i = 1; i < 10; i++)
            {
                board[x][y] = i + 48;
                Dfs(board, n + 1);
                if (flag == true)
                    return;
                board[x][y] = '.';
            }
        }
    }

    bool JudgeIsNoWant(vector<vector<char>> &board, int n)
    {
        int x = n / 9;
        int y = n % 9;

        for (size_t i = 0; i < 9; i++)
        {
            if (board[x][i] == board[x][y] && i != y)
                return false;
            if (board[i][y] == board[x][y] && i != x)
                return false;
        }

        for (int i = x / 3 * 3; i < x / 3 * 3 + 3; i++)
            for (int j = y / 3 * 3; j < y / 3 * 3 + 3; j++)
                if (board[i][j] == board[x][y] && (i != x || j != y))
                    return false;

        return true;
    }
};

int main()
{
	Solution s;
	vector<vector<char>>board = {
			{'5','3','.','.','7','.','.','.','.'},
		    {'6','.','.','1','9','5','.','.','.'},
		    {'.','9','8','.','.','.','.','6','.'},
		    {'8','.','.','.','6','.','.','.','3'},
		    {'4','.','.','8','.','3','.','.','1'},
		    {'7','.','.','.','2','.','.','.','6'},
		    {'.','6','.','.','.','.','2','8','.'},
		    {'.','.','.','4','1','9','.','.','5'},
		    {'.','.','.','.','8','.','.','7','9'}};
    
    s.solveSudoku(board);
	for (auto sudoku : board){
		for (auto row : sudoku)
			cout << row << " ";
		cout <<endl;
	}
	return 0;
} 

#include <bits/stdc++.h>
using namespace std;

class Solution
{
public:
	void solveSudoku(vector<vector<char>> &board)
	{
		int size = board.size();
		vector<vector<bool>> rows(size, vector<bool>(10));
		vector<vector<bool>> cols(size, vector<bool>(10));
		vector<vector<bool>> boxes(size, vector<bool>(10));
		for (int i = 0; i < size; i++)
		{
			for (int j = 0; j < size; j++)
			{
				if (board[i][j] != '.')
				{
					int num = board[i][j] - '0';
					int idx = i / 3 * 3 + j / 3;
					rows[i][num] = true;
					cols[j][num] = true;
					boxes[idx][num] = true;
				}
			}
		}
		dfs(board, 0, rows, cols, boxes);
	}
private:
	bool valid(int num, int row, int col, int idx, vector<vector<bool>> &rows,
			   vector<vector<bool>> &cols, vector<vector<bool>> &boxes)
	{
		return !rows[row][num] && !cols[col][num] && !boxes[idx][num];
	}
	bool dfs(vector<vector<char>> &board, int size, vector<vector<bool>> &rows,
			 vector<vector<bool>> &cols, vector<vector<bool>> &boxes)
	{
		if (size == 9 * 9)
		{
			return true;
		}
		else
		{
			bool ok = false;
			int row = size / 9;
			int col = size % 9;
			int idx = row / 3 * 3 + col / 3;
			if (board[row][col] == '.')
			{
				for (int i = 1; i <= 9; i++)
				{
					if (valid(i, row, col, idx, rows, cols, boxes))
					{
						board[row][col] = i + '0';
						rows[row][i] = true;
						cols[col][i] = true;
						boxes[idx][i] = true;
						ok = dfs(board, size + 1, rows, cols, boxes);
						if (!ok)
						{
							rows[row][i] = false;
							cols[col][i] = false;
							boxes[idx][i] = false;
							board[row][col] = '.';
						}
					}
				}
			}
			else
			{
				ok = dfs(board, size + 1, rows, cols, boxes);
			}
			return ok;
		}
	}
};

int main()
{
	Solution s;
	vector<vector<char>>board = {
			{'5','3','.','.','7','.','.','.','.'},
		    {'6','.','.','1','9','5','.','.','.'},
		    {'.','9','8','.','.','.','.','6','.'},
		    {'8','.','.','.','6','.','.','.','3'},
		    {'4','.','.','8','.','3','.','.','1'},
		    {'7','.','.','.','2','.','.','.','6'},
		    {'.','6','.','.','.','.','2','8','.'},
		    {'.','.','.','4','1','9','.','.','5'},
		    {'.','.','.','.','8','.','.','7','9'}};
    
    s.solveSudoku(board);
	for (auto sudoku : board){
		for (auto row : sudoku)
			cout << row << " ";
		cout <<endl;
	}
	return 0;
}

以下代码错？不显示结果，输出起始board

#include <bits/stdc++.h>
using namespace std;

class Solution
{
public:
    int row[9][9], col[9][9], block[9][9];
    void solveSudoku(vector<vector<char>> &board)
    {
        for (int i = 0; i < 9; ++i)
        {
            for (int j = 0; j < 9; ++j)
            {
                if (board[i][j] == '.')
                    continue;
                int num = board[i][j] - '1';
                row[i][num] = col[j][num] = block[i / 3 * 3 + j / 3][num] = 1;
            }
        }
        dfs(board, 0, 0);
    }
    bool dfs(vector<vector<char>> &board, int r, int c)
    {
        if (r > 8)
            return true;
        if (board[r][c] == '.')
        {
            for (int i = 0; i < 9; ++i)
            {
                if (row[r][i] || col[c][i] || block[r / 3 * 3 + c / 3][i])
                    continue;
                board[r][c] = i + 1 + '0';
                row[r][i] = col[c][i] = block[r / 3 * 3 + c / 3][i] = 1;

                if (dfs(board, r + (c + 1) / 9, (c + 1) % 9))
                    return true;

                board[r][c] = '.';
                row[r][i] = col[c][i] = block[r / 3 * 3 + c / 3][i] = 0;
            }
        }
        else
            return dfs(board, r + (c + 1) / 9, (c + 1) % 9);
        return false;
    }
};

int main()
{
	Solution s;
	vector<vector<char>>board = {
			{'5','3','.','.','7','.','.','.','.'},
		    {'6','.','.','1','9','5','.','.','.'},
		    {'.','9','8','.','.','.','.','6','.'},
		    {'8','.','.','.','6','.','.','.','3'},
		    {'4','.','.','8','.','3','.','.','1'},
		    {'7','.','.','.','2','.','.','.','6'},
		    {'.','6','.','.','.','.','2','8','.'},
		    {'.','.','.','4','1','9','.','.','5'},
		    {'.','.','.','.','8','.','.','7','9'}};
    
    s.solveSudoku(board);
	for (auto sudoku : board){
		for (auto row : sudoku)
			cout << row << " ";
		cout <<endl;
	}
	return 0;
}

51. N 皇后

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例 1：

输入：n = 4
输出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

输入：n = 1
输出：[["Q"]]

提示：

  • 1 <= n <= 9
  • 皇后彼此不能相互攻击，也就是说：任何两个皇后都不能处于同一条横行、纵行或斜线上。
#include <bits/stdc++.h>
using namespace std;

class Solution
{
public:
    vector<vector<string>> solveNQueens(int n)
    {
        vector<vector<string>> res;
        vector<int> stack(n);
        vector<string> solution(n, string(n, '.'));
        dfs(n, 0, stack, solution, res);
        return res;
    }

private:
    void dfs(int n, int row, vector<int> &stack, vector<string> &solution, vector<vector<string>> &res)
    {
        if (row == n)
        {
            res.push_back(solution);
        }
        else
        {
            for (int i = 0; i < n; i++)
            {
                if (row == 0 || !conflict(stack, row, i))
                {
                    solution[row][i] = 'Q';
                    stack[row] = i;
                    dfs(n, row + 1, stack, solution, res);
                    solution[row][i] = '.';
                }
            }
        }
    }
    bool conflict(vector<int> &stack, int row, int col)
    {
        for (int i = 0; i < row; i++)
        {
            if (col == stack[i] || abs(row - i) == abs(col - stack[i]))
            {
                return true;
            }
        }
        return false;
    }
};

int main()
{
	Solution s;
	int i = 0;
	for (auto res : s.solveNQueens(4)){
		cout << ++i << endl;
		for (auto item : res)
			cout << item << " ";
		cout << endl;
	}
	cout << endl;
	
	return 0;
} 

#include <bits/stdc++.h>
using namespace std;

class Solution
{
public:
    vector<vector<string>> res;
    vector<vector<string>> solveNQueens(int n)
    {
        vector<string> board(n, string(n, '.'));
        backtrack(board, 0);
        return res;
    }

    void backtrack(vector<string> &board, int row)
    {
        if (row == board.size())
        {
            res.push_back(board);
            return;
        }
        int n = board[row].size();
        for (int col = 0; col < n; col++)
        {
            if (!isValid(board, row, col))
            {
                continue;
            }
            board[row][col] = 'Q';
            backtrack(board, row + 1);
            board[row][col] = '.';
        }
    }

    bool isValid(vector<string> &board, int row, int col)
    {
        int n = board.size();
        for (int i = 0; i < row; i++)
        {
            if (board[i][col] == 'Q')
            {
                return false;
            }
        }
        for (int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++)
        {
            if (board[i][j] == 'Q')
            {
                return false;
            }
        }
        for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--)
        {
            if (board[i][j] == 'Q')
            {
                return false;
            }
        }
        return true;
    }
};

int main()
{
	Solution s;
	int i = 0;
	for (auto res : s.solveNQueens(4)){
		cout << ++i << endl;
		for (auto item : res)
			cout << item << " ";
		cout << endl;
	}
	cout << endl;
	
	return 0;
} 

#include <bits/stdc++.h>
using namespace std;

class Solution
{
public:
    bool isValue(vector<int> &pos, int row, int col)
    {
        for (int i = 0; i < row; ++i)
        {
            if (col == pos[i] || abs(row - i) == abs(col - pos[i]))
                return false;
        }
        return true;
    }
    void solveNQueensDFS(vector<int> &pos, int row, vector<vector<string>> &ans)
    {
        int n = pos.size();
        if (row == n)
        {
            vector<string> tmp(n, string(n, '.'));
            for (int i = 0; i < n; ++i)
                tmp[i][pos[i]] = 'Q';
            ans.push_back(tmp);
        }
        else
        {
            for (int col = 0; col < n; ++col)
            {
                if (isValue(pos, row, col))
                {
                    pos[row] = col;
                    solveNQueensDFS(pos, row + 1, ans);
                    pos[row] = -1;
                }
            }
        }
    }
    vector<vector<string>> solveNQueens(int n)
    {
        vector<int> pos(n, -1);
        vector<vector<string>> ans;
        solveNQueensDFS(pos, 0, ans);
        return ans;
    }
};

int main()
{
	Solution s;
	int i = 0;
	for (auto res : s.solveNQueens(4)){
		cout << ++i << endl;
		for (auto item : res)
			cout << item << " ";
		cout << endl;
	}
	cout << endl;
	
	return 0;
}

52. N皇后 II

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回 n 皇后问题 不同的解决方案的数量。

示例 1：

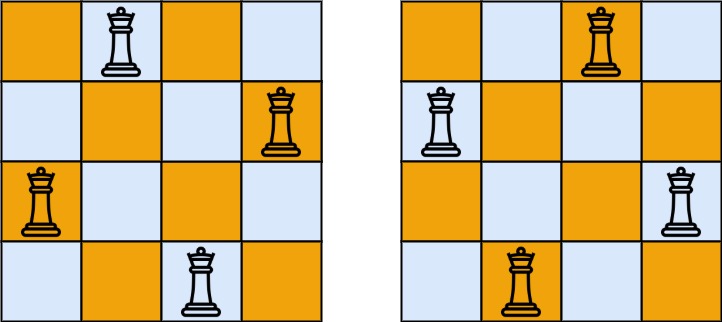
输入：n = 4
输出：2
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

输入：n = 1
输出：1

提示：

  • 1 <= n <= 9
  • 皇后彼此不能相互攻击，也就是说：任何两个皇后都不能处于同一条横行、纵行或斜线上。

#include <bits/stdc++.h>
using namespace std;

class Solution
{
public:
    int totalNQueens(int n)
    {
        vector<int> stack(n);
        return dfs(n, 0, stack);
    }

private:
    int dfs(int n, int row, vector<int> &stack)
    {
        int count = 0;
        if (row == n)
        {
            return count + 1;
        }
        else
        {
            for (int i = 0; i < n; i++)
            {
                if (row == 0 || !conflict(stack, row, i))
                {
                    stack[row] = i;
                    count += dfs(n, row + 1, stack);
                }
            }
            return count;
        }
    }
    bool conflict(vector<int> &stack, int row, int col)
    {
        for (int i = 0; i < row; i++)
        {
            if (col == stack[i] || abs(row - i) == abs(col - stack[i]))
            {
                return true;
            }
        }
        return false;
    }
};

int main()
{
	Solution s;
	cout << s.totalNQueens(1) << endl;
	cout << s.totalNQueens(4) << endl;
	cout << s.totalNQueens(8) << endl;
	
	return 0;
} 

#include <bits/stdc++.h>
using namespace std;

class Solution
{
public:
    bool isvalid(vector<string> &temp, int i, int j)
    { //判断棋盘是否有效
        //for (int k = 0; k<temp[i].size(); ++k){//判断行。不用判断行了，每行放一个之后就会递归到下一行了
        //	if (temp[i][k] == 'Q') return false;
        //}
        for (int k = 0; k < i; ++k)
        { //判断列
            if (temp[k][j] == 'Q')
                return false;
        }
        for (int p = i - 1, q = j - 1; p >= 0 && q >= 0; --p, --q)
        { //判断左上对角线
            if (temp[p][q] == 'Q')
                return false;
        }
        for (int p = i - 1, q = j + 1; p >= 0 && q < temp.size(); --p, ++q)
        { //判断右上对角线
            if (temp[p][q] == 'Q')
                return false;
        }
        return true;
    }

    int dfs(int &count, vector<string> &temp, int i, int n)
    {
        if (i == n)
            return ++count;

        for (int j = 0; j < n; ++j)
        {
            if (isvalid(temp, i, j))
            {
                temp[i][j] = 'Q'; //递归前修改
                dfs(count, temp, i + 1, n);
            }
            temp[i][j] = '.'; //递归后恢复
        }
        return count;
    }

    int totalNQueens(int n)
    {
        int count = 0;
        string aa;
        for (int i = 0; i < n; ++i)
            aa += '.';
        vector<string> temp(n, aa);
        return dfs(count, temp, 0, n);
    }
};

int main()
{
	Solution s;
	cout << s.totalNQueens(1) << endl;
	cout << s.totalNQueens(4) << endl;
	cout << s.totalNQueens(8) << endl;
	
	return 0;
} 

#include <bits/stdc++.h>
using namespace std;

class Solution
{
public:
    void recurse(vector<string> solution, int pos, vector<vector<bool>> validPos, int &result)
    {
        int n = solution[0].size();
        if (pos == n)
        {
            result++;
            return;
        }

        for (int i = 0; i < n; i++)
        {
            if (!validPos[pos][i])
                continue;

            vector<vector<bool>> newPos = validPos;
            for (int j = pos; j < n; j++)
            {
                newPos[j][i] = false;
                if (i - j + pos >= 0)
                    newPos[j][i - j + pos] = false;
                if (i + j - pos < n)
                    newPos[j][i + j - pos] = false;
            }
            solution[pos][i] = 'Q';

            recurse(solution, pos + 1, newPos, result);
            solution[pos][i] = '.';
        }

        return;
    }

    int totalNQueens(int n)
    {
        int result = 0;
        vector<string> solution(n, string(n, '.'));
        vector<vector<bool>> validPos = vector<vector<bool>>(n, vector<bool>(n, true));

        recurse(solution, 0, validPos, result);

        return result;
    }
};

int main()
{
	Solution s;
	cout << s.totalNQueens(1) << endl;
	cout << s.totalNQueens(4) << endl;
	cout << s.totalNQueens(8) << endl;
	
	return 0;
}

89. 格雷编码

格雷编码是一个二进制数字系统，在该系统中，两个连续的数值仅有一个位数的差异。

给定一个代表编码总位数的非负整数 n，打印其格雷编码序列。即使有多个不同答案，你也只需要返回其中一种。

格雷编码序列必须以 0 开头。

示例 1:

输入: 2
输出: [0,1,3,2]
解释:00 - 001 - 111 - 310 - 2对于给定的 n，其格雷编码序列并不唯一。例如，[0,2,3,1] 也是一个有效的格雷编码序列。00 - 010 - 211 - 301 - 1

示例 2:

输入: 0
输出: [0]
解释: 我们定义格雷编码序列必须以 0 开头。给定编码总位数为 n 的格雷编码序列，其长度为 2^n。当 n = 0 时，长度为 2^0 = 1。因此，当 n = 0 时，其格雷编码序列为 [0]。
#include <bits/stdc++.h>
using namespace std;

class Solution
{
public:
    vector<int> grayCode(int n)
    {
        int size = 1 << n;
        vector<int> res;
        for (int i = 0; i < size; i++)
        {
            int graycode = i ^ (i >> 1);
            res.push_back(graycode);
        }
        return res;
    }
};

int main()
{
	Solution s;
	vector<int> res = s.grayCode(2);
	copy(res.begin(), res.end(), ostream_iterator<int>(cout," "));
	cout << endl;

	res = s.grayCode(0);
	copy(res.begin(), res.end(), ostream_iterator<int>(cout," "));
	
	return 0;
} 
#include <bits/stdc++.h>
using namespace std;

class Solution
{
public:
    vector<int> grayCode(int n)
    {
        vector<int> res;
        for (int i = 0; i < (int)pow(2, n); i++)
            res.push_back(i ^ (i >> 1));
        return res;
    }
};

int main()
{
	Solution s;
	vector<int> res = s.grayCode(2);
	copy(res.begin(), res.end(), ostream_iterator<int>(cout," "));
	cout << endl;

	res = s.grayCode(0);
	copy(res.begin(), res.end(), ostream_iterator<int>(cout," "));
	
	return 0;
} 

#include <bits/stdc++.h>
using namespace std;

class Solution
{
public:
    vector<int> grayCode(int n)
    {
        vector<int> res;
        res.push_back(0);
        if (n == 0)
            return res;
        int head = 1;
        for (int i = 0; i < n; i++)
        {
            for (int j = res.size() - 1; j >= 0; j--)
            {
                res.push_back(head + res[j]);
            }
            head <<= 1;
        }
        return res;
    }
};

int main()
{
	Solution s;
	vector<int> res = s.grayCode(2);
	copy(res.begin(), res.end(), ostream_iterator<int>(cout," "));
	cout << endl;

	res = s.grayCode(0);
	copy(res.begin(), res.end(), ostream_iterator<int>(cout," "));
	
	return 0;
}

90. 子集 II

给你一个整数数组 nums ，其中可能包含重复元素，请你返回该数组所有可能的子集（幂集）。

解集 不能 包含重复的子集。返回的解集中，子集可以按 任意顺序 排列。

示例 1：

输入：nums = [1,2,2]
输出：[[],[1],[1,2],[1,2,2],[2],[2,2]]

示例 2：

输入：nums = [0]
输出：[[],[0]]

提示：

  • 1 <= nums.length <= 10
  • -10 <= nums[i] <= 10

#include <bits/stdc++.h>
using namespace std;

class Solution
{
public:
    vector<vector<int>> subsetsWithDup(vector<int> &nums)
    {

        vector<vector<int>> result;
        vector<int> item;
        set<vector<int>> rset;
        result.push_back(item);
        sort(nums.begin(), nums.end());
        CreatSet(0, result, item, nums, rset);
        return result;
    }
    void CreatSet(int i, vector<vector<int>> &result,
                  vector<int> &item, vector<int> &nums,
                  set<vector<int>> &rset)
    {
        if (i >= nums.size())
            return;
        item.push_back(nums[i]);
        if (rset.find(item) == rset.end())
        {
            rset.insert(item);
            result.push_back(item);
        }
        CreatSet(i + 1, result, item, nums, rset);
        item.pop_back();
        CreatSet(i + 1, result, item, nums, rset);
    }
};

int main()
{
	Solution s;
	vector<int> nums = {1,2,2};
	vector<vector<int>> res = s.subsetsWithDup(nums);
	
	for (auto r:res){
		copy(r.begin(), r.end(), ostream_iterator<int>(cout, " "));
		cout << endl;
	}

	return 0;
} 

#include <bits/stdc++.h>
using namespace std;

class Solution
{
public:
    vector<vector<int>> subsetsWithDup(vector<int> &nums)
    {

        sort(nums.begin(), nums.end());
        vector<vector<int>> res;
        vector<int> cur;
        for (int i = 0; i <= nums.size(); i++)
        {
            dfs(res, cur, nums, 0, i);
        }
        return res;
    }

    void dfs(vector<vector<int>> &res, vector<int> &cur, vector<int> &nums, int begin, int n)
    {
        if (cur.size() == n)
        {
            res.push_back(cur);
            return;
        }
        for (int i = begin; i < nums.size(); i++)
        {

            if (i > begin && nums[i] == nums[i - 1])
                continue;
            cur.push_back(nums[i]);
            dfs(res, cur, nums, i + 1, n);
            cur.pop_back();
        }
        return;
    }
};

int main()
{
	Solution s;
	vector<int> nums = {1,2,2};
	vector<vector<int>> res = s.subsetsWithDup(nums);
	
	for (auto r:res){
		copy(r.begin(), r.end(), ostream_iterator<int>(cout, " "));
		cout << endl;
	}

	return 0;
} 

#include <bits/stdc++.h>
using namespace std;

class Solution
{
public:
    vector<vector<int>> ans;
    vector<int> cur;
    vector<int> v;
    void dfs(int depth)
    {
        ans.push_back(cur);
        if (depth == v.size())
            return;
        for (int i = depth; i < v.size(); ++i)
        {
            if (i > depth && v[i] == v[i - 1])
                continue;
            cur.push_back(v[i]);
            dfs(i + 1);
            cur.pop_back();
        }
    }
    vector<vector<int>> subsetsWithDup(vector<int> &nums)
    {
        sort(nums.begin(), nums.end());
        v = nums;
        dfs(0);
        return ans;
    }
};

string VectorToString(vector<int> vec, string split=",")
{
    if (vec.size()==0) return "[]";
    string res = "[";
    for (auto n:vec)
        res += to_string(n) + split;
    return res.substr(0, res.length() - split.size()) + "]";
}

int main()
{
	Solution s;
	vector<int> nums = {1,2,2};
	vector<vector<int>> res = s.subsetsWithDup(nums);
	
	for (auto r:res){
		cout << VectorToString(r) << " ";
	}

	return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/372326.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

java spring AOP 完全注解开发

java spring AOP 完全注解开发

我们先创建一个项目 然后引入java spring aop的依赖 然后 在src下创建目录 我这里 直接就叫 Aop了 下面创建一个User类 参考代码如下 package Aop;import org.springframework.stereotype.Component;Component public class User {public void add(){System.out.println(&qu…
阅读更多...
Allegro如何锁定报表界面操作指导

Allegro如何锁定报表界面操作指导

Allegro如何锁定报表界面操作指导 用Allegro做PCB设计的时候，进行测量的时候，比如测量器件两个PIN中间的间距，如下图，会有一个报表显示 但是当运行下一个命令的时候，报表会被自动关闭掉。 但是有时我们需要报表界面仍被保留 下面介绍如何将报表界面进行锁定，不受下一个…
阅读更多...
新氧2023年财务业绩预测：退市风险大幅降低，收入增长将放缓

新氧2023年财务业绩预测：退市风险大幅降低，收入增长将放缓

来源&#xff1a;猛兽财经 作者&#xff1a;猛兽财经 公司进展 与新氧&#xff08;SY&#xff09;有关的两个重要积极进展值得一提。 第一个积极进展是新氧的退市风险已在很大程度上降低。 2023年1月6日&#xff0c;新氧披露&#xff0c;它已经“重新符合纳斯达克规定的股价每…
阅读更多...
AIR32F103(九) CAN总线的通信和ID过滤机制及实例

AIR32F103(九) CAN总线的通信和ID过滤机制及实例

目录 AIR32F103(一) 合宙AIR32F103CBT6开发板上手报告AIR32F103(二) Linux环境和LibOpenCM3项目模板AIR32F103(三) Linux环境基于标准外设库的项目模板AIR32F103(四) 27倍频216MHz,CoreMark跑分测试AIR32F103(五) FreeRTOSv202112核心库的集成和示例代码AIR32F103(六) ADC,I2S…
阅读更多...
Zookeeper完全分布式集群服务

Zookeeper完全分布式集群服务

准备好3台服务器:[x]A-> centos7s:192.168.19.1[x]B-> centos7_1:192.168.19.2[x]C-> centos7_2:192.168.19.3配置Zookeeper安装目录在3台宿主机配置zookeeper安装目录&#xff1a;/docker/develop/zookeeper并且在文件夹创建 data 和logs 目录&#xff1a;mkdir -p /…
阅读更多...
STM32Cube串口USART发送接收数据

STM32Cube串口USART发送接收数据

本文代码使用 HAL 库。 文章目录前言一、USART 同步/异步串行接收/发送器二、USART 原理图三、CubeMX 创建工程四、usart.c 文件解析五&#xff0c;设计实验&#xff1a;在 串口输入字符点亮led实验现象&#xff1a;总结前言 这篇文章介绍 实现 USART 异步模式下 通过 串口助手…
阅读更多...
去了字节跳动，才知道年薪40W的测试居然有这么多？

去了字节跳动，才知道年薪40W的测试居然有这么多？

今年大环境不好&#xff0c;内卷的厉害&#xff0c;薪资待遇好的工作机会更是难得。最近脉脉职言区有一条讨论火了&#xff1a; 哪家互联网公司薪资最‘厉害’&#xff1f; 下面的评论多为字节跳动&#xff0c;还炸出了很多年薪40W的测试工程师 我只想问一句&#xff0c;现在的…
阅读更多...
【设计模式】 观察者模式介绍及C代码实现

【设计模式】 观察者模式介绍及C代码实现

【设计模式】 观察者模式介绍及C代码实现 背景 在软件构建过程中&#xff0c;我们需要为某些对象建立一种“通知依赖关系”&#xff0c;即一个对象&#xff08;目标对象&#xff09;的状态发生改变&#xff0c;所有的依赖对象&#xff08;观察者对象&#xff09;都将得到通知。…
阅读更多...
连续隐身四天、被传退出德云社，于谦未参加相声大会的原因找到了

连续隐身四天、被传退出德云社，于谦未参加相声大会的原因找到了

欲戴皇冠&#xff0c;必受其重。意思就是一个人拥有一定的地位和声望&#xff0c;就会承担由此带来的责任和压力。 就拿德云社郭德纲搭档于谦来说&#xff0c;虽然他是一个谦虚低调的人&#xff0c;但是因为郭德纲老师名气太大&#xff0c;也让于谦伴随着一起名声鹊起。于谦老师…
阅读更多...
chatgpt的原理 第三部分

chatgpt的原理 第三部分

对话 我们是如何学会中文的&#xff1f;从0岁开始&#xff0c;听、说&#xff0c;也就是对话。 我们是如何学外语的&#xff1f;看教材&#xff0c;听广播&#xff0c;背单词。唯独缺少了对话&#xff01;正是因为缺少了对话这个高效的语言学习方式&#xff0c;所以我们的英语…
阅读更多...
8个小程序开源项目助你快速搭建小程序

8个小程序开源项目助你快速搭建小程序

今天和大家分享几个小程序开源项目, 帮助我们轻松搭建自己的小程序应用. 我会从大家最熟悉的小程序UI组件, 到可视化库, 再到完整项目, 一一和大家介绍.小程序UI组件库小程序多端开发框架小程序可视化图表库经典小程序开源项目小程序UI组件库1. vant-weappVant Weapp 是移动端 …
阅读更多...
MXNet中使用卷积神经网络textCNN对文本进行情感分类

MXNet中使用卷积神经网络textCNN对文本进行情感分类

在图像识别领域&#xff0c;卷积神经网络是非常常见和有用的&#xff0c;我们试图将它应用到文本的情感分类上&#xff0c;如何处理呢&#xff1f;其实思路也是一样的&#xff0c;图片是二维的&#xff0c;文本是一维的&#xff0c;同样的&#xff0c;我们使用一维的卷积核去处…
阅读更多...
LLVM程序分析与编译转换框架论文分享

LLVM程序分析与编译转换框架论文分享

LLVM 2004年论文原文 概述 本文描述了 LLVM&#xff08;低级虚拟机&#xff09;&#xff0c;一种编译器框架&#xff0c;旨在通过在编译时、链接时、运行时&#xff0c;以及运行之间的空闲时间。 LLVM 以静态单一赋值 (SSA) 形式定义了一种通用的低级代码表示&#xff0c;具有…
阅读更多...
多区域的OSPF实战配置

多区域的OSPF实战配置

多区域的OSPF实战配置 需求 如图配置设备的接口IP地址如图规划OSPF网络的区域要求每个设备的 router-id 都是 x.x.x.x&#xff08;x是每个路由器的名字&#xff09;确保不同的PC之间可以互通 拓扑图 配置命令 PC1&#xff1a; 192.168.1.1 255.255.255.0 192.168.1.254PC2:…
阅读更多...
【手把手一起学习】(六) Altium Designer 20 STM32核心板Demo----PCB设计

【手把手一起学习】(六) Altium Designer 20 STM32核心板Demo----PCB设计

1 PCB设计 PCB设计是制作STM32核心板的关键步骤&#xff0c;其关系到最终生产厂家制作的电路板能否正常使用&#xff0c;PCB设计包括布局&#xff0c;裁板&#xff0c;布线&#xff0c;覆铜&#xff0c;DRC检查等&#xff0c;其中要求、细节、技巧比较多&#xff0c;以后会更详…
阅读更多...
redis（7）哈希Hash

redis（7）哈希Hash

哈希Hash Redis hash 是一个键值对集合。 Redis hash 是一个 string 类型的 field 和 value 的映射表&#xff0c;hash 特别适合用于存储对象。 类似 Java 里面的 Map<String,Object>。 用户 ID 为查找的 key&#xff0c;存储的 value 用户对象包含姓名&#xff0c;年…
阅读更多...
西北工业大学大学物理（II）选填解析2019-2020期末

西北工业大学大学物理（II）选填解析2019-2020期末

2 又是考查“一个电子和一个光子具有相同的波长&#xff0c;则二者动量相等。”4 斯特恩盖拉赫实验&#xff0c;原子的自旋磁矩取向量子化。7 通常我们感受不到电子的波动性。因为其波长短&#xff0c;其实也就是粒子运动速率高。10 考查无限长直导线周围B分布。常见的模型要记…
阅读更多...
【035】基于Vue的电商推荐管理系统（含源码数据库、超详细论文）

【035】基于Vue的电商推荐管理系统（含源码数据库、超详细论文）

摘 要&#xff1a;基于Vue&#xff0b;Nodejs&#xff0b;mysql的电商推荐管理系统&#xff0c;这个项目论文超详细&#xff0c;er图、接口文档、功能展示、技术栈等说明特别全&#xff01;&#xff01;&#xff01; &#xff08;文末附源码数据库、课设论文获取方式&#xff0…
阅读更多...
xgboost学习-原理

xgboost学习-原理

文章目录一、xgboost库与XGB的sklearn APIXGBoost的三大板块二、梯度提升树提升集成算法&#xff1a;重要参数n_estimators三、有放回随机抽样&#xff1a;重要参数subsample四、迭代决策树&#xff1a;重要参数eta总结一、xgboost库与XGB的sklearn API 现在&#xff0c;我们有…
阅读更多...
【ROS学习笔记4】话题通信

【ROS学习笔记4】话题通信

【ROS学习笔记4】话题通信 文章目录【ROS学习笔记4】话题通信零、话题通信概述一、话题通信的理论模型二、话题通信基本操作的Cpp实现三、话题通信基本操作的Python实现四、话题通信自定义msg五、话题通信自定义msg调用的Cpp实现六、话题通信自定义msg的Python实现七、Referenc…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023