题目链接
Leetcode.2385 感染二叉树需要的总时间 Rating : 1711
题目描述
给你一棵二叉树的根节点 root,二叉树中节点的值 互不相同 。另给你一个整数 start。在第 0分钟,感染 将会从值为 start的节点开始爆发。
每分钟,如果节点满足以下全部条件,就会被感染:
- 节点此前还没有感染。
- 节点与一个已感染节点相邻。
返回感染整棵树需要的分钟数。
示例 1:
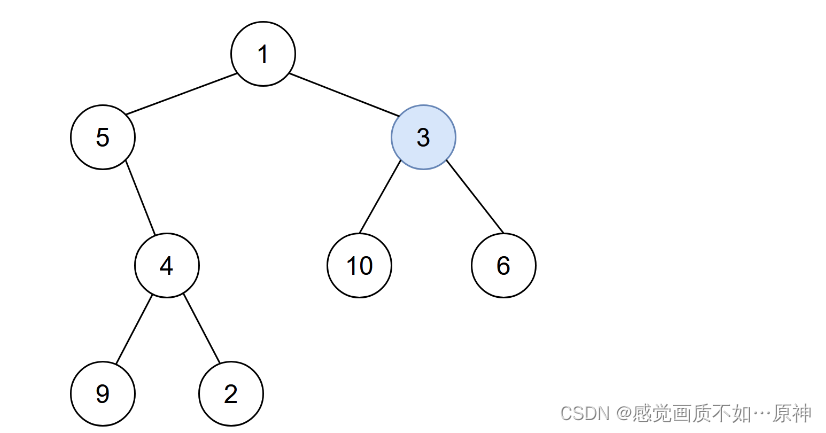
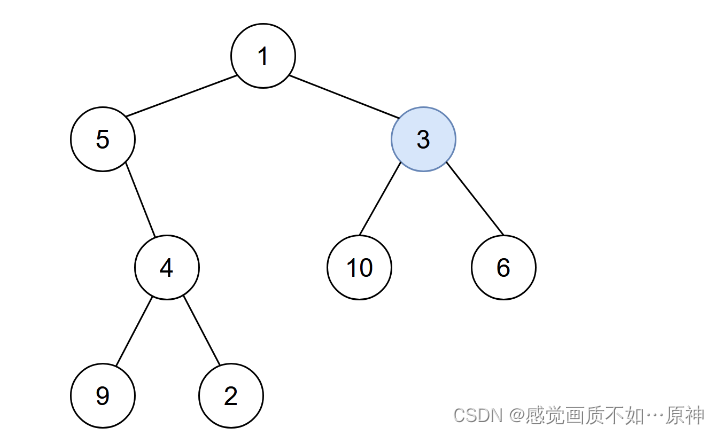
输入:root = [1,5,3,null,4,10,6,9,2], start = 3
输出:4
解释:节点按以下过程被感染:
- 第 0 分钟:节点 3
- 第 1 分钟:节点 1、10、6
- 第 2 分钟:节点5
- 第 3 分钟:节点 4
- 第 4 分钟:节点 9 和 2 感染整棵树需要 4 分钟,所以返回 4 。
示例 2:

输入:root = [1], start = 1
输出:0
解释:第 0 分钟,树中唯一一个节点处于感染状态,返回 0 。
提示:
- 树中节点的数目在范围 [1, 1 0 5 10^5 105] 内
- 1 < = N o d e . v a l < = 1 0 5 1 <= Node.val <= 10^5 1<=Node.val<=105
- 每个节点的值 互不相同
- 树中必定存在值为
start的节点
解法一:DFS建图 + BFS
用一个集合 g保存 图的边,在 DFS 的过程中,加入边。例如 1 -> 5 , 5 -> 1 , 1 -> 3 , 3 -> 1。
接着再从起点 start开始 BFS 求最短的路径,即感染整棵树的时间。
时间复杂度: O ( n ) O(n) O(n)
代码:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
//g 用来存储图的边
unordered_map<int,vector<int>> g;
//dfs 建图
void dfs(TreeNode* root){
if(root==nullptr) return;
int a = root->val;
if(root->left != nullptr){
int b = root->left->val;
g[a].push_back(b);
g[b].push_back(a);
}
if(root->right != nullptr){
int b = root->right->val;
g[a].push_back(b);
g[b].push_back(a);
}
dfs(root->left);
dfs(root->right);
}
int amountOfTime(TreeNode* root, int start) {
dfs(root);
queue<int> q;
//记录已经被感染过的点
unordered_set<int> vis;
int ans = 0;
//加入起点
q.push(start);
vis.insert(start);
//bfs 求整棵树被感染的时间 就是求 从 start 开始的最长路径。
while(!q.empty()){
int sz = q.size();
for(int i = 0;i < sz;i++){
auto u = q.front();
q.pop();
for(auto v:g[u]){
if(vis.count(v)) continue;
vis.insert(v);
q.push(v);
}
}
ans++;
}
return ans - 1;
}
};
解法二:DFS
当 start是根结点时,整棵树被感染的时间就是树的高度(1)。
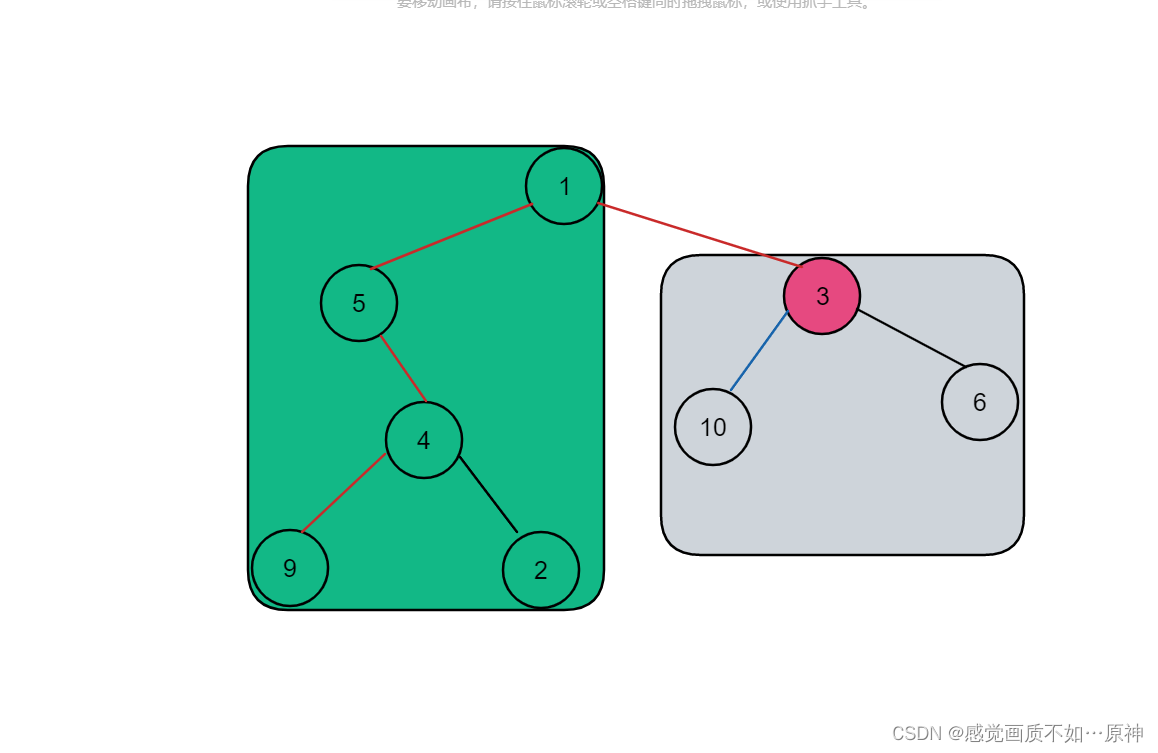
当 start不是根结点时,整棵树被感染的时间就是 以start为根结点的树的高度 和 start到根结点的距离加上 + 另一棵子树的高度,这两者取最大值。
时间复杂度: O ( n ) O(n) O(n)
代码:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int depth = -1;
int ans = 0;
//返回以 root 为根结点的树高度
int dfs(TreeNode* root,int level,int start){
if(root == nullptr) return 0;
//先搜左子树,l 是左子树的高度
int l = dfs(root->left,level + 1,start);
//记录初始感染结点在第 几 层
if(root->val == start) depth = level;
//判断初始感染结点是否在左子树
bool inLeft = depth != -1;
//再搜右子树 , r 是右子树的高度
int r = dfs(root->right,level+1,start);
//如果此时遇到 start ,就先记录 以它为根结点的树高 , 因为我们是自底向上递归的,所以 l 和 r
//现在时已经计算出来的了
if(root->val == start) ans = max(ans,max(l,r));
//如果start在左子树,那就更新 当前结点到根结点的距离 + 根结点右子树的距离。start在右子树也是
//一样的逻辑
//需要注意的是,实际上更新的答案应该是 当前结点 cur 回溯到根结点时,此时的level = 0,depth我们递归的过程中已经记录下来了,此时根结点root 的右子树高度r 才是整棵树右子树的高度
//此时的 depth - level + r 才是我们最终需要的答案,但是实际上这些中间过程的结点产生的答案也并不会影响我们最终的答案。
if(inLeft) ans = max(ans,depth - level + r);
else ans = max(ans,depth - level + l);
return max(l,r)+1;
}
int amountOfTime(TreeNode* root, int start) {
dfs(root,0,start);
return ans;
}
};