蓄水池抽样,也称水塘抽样,是随机抽样算法的一种。
基本抽样问题
有一批数据(假设为一个数组,可以逐个读取),要从中随机抽取一个数字,求抽得的数字下标。
常规的抽样方法是,先读取所有的数字,记录数字的总个数,记为n。然后产生一个0 ~ n - 1范围内的随机数即可,即随机抽取的数字下标index为:
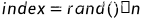
其中,rand为随机数产生函数。
但是上述常规抽样方法,有一个局限性就是,必须读取完所有的数字之后才可以计算下标。
一方面,如果数据量很大,一次性读入所有的数据,需要很大的内存。另外一方面,很多流式数据,往往都是不断在读取数据,如果要读完所有的数据,还需要额外记录度过的数据。
那么,能不能边读数据边计算,并且度过的数据不要记录了呢?
蓄水池抽样基本算法
这里就要用到今天要讲的蓄水池抽样算法,用index记录最终得到随机数下标,该算法简述如下:
从前往后不断读取数字,读到第i(从0开始)个数字时,在[0, i]范围内产生一个随机数r,如果r = 0,那么index = i,否则index维持原来的的值,那么最终index就是产生的随机数的下标。
下面来证明这个算法的正确性,证明算法的正确性,即使要证明每个数字抽到的概率相等。假设数字的中个数为n,那么这些数字的下标为0 ~ n - 1,设抽到下标为i的数字的概率为P(i),根据上面的描述,要抽到下标为i的数字,要满足的条件为:
在读到第i个数字时,[0, i]范围内产生的随机数为0,这样index = i
在读到第i个数字之后的数字时,不能再产生随机数0(否则index就为k了)
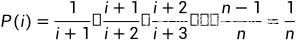

从上面的计算可以看到,每个数字抽到的概率为1/n,因此该抽样的方法是正确的。
很多人有一点疑惑,通过上面的方法,一定会抽到某个数字吗?
答案是肯定的,因为在读到第0个数字时,从[0,0]中产生一个随机数,肯定是0。因此,下标为0的梳子一开始肯定会被选中,如果后续没有其它数字选中的话,就是下标为0的数字了,从而保证一定有一个数字被选中。
蓄水池抽样算法的变式
假如并不是从所有的数字中抽取,而是从满足某些条件的数字中抽取。假如这些数字中有多个数字x,要从所有的数字x中抽出一个数字,求最后抽得的数字x的下标。
只需要将上面方法中的i换成x的计数就好:
从前往后不断读取数字,读到第k个数字时,若该数字为x,设为第i个x,在[0, i]范围内产生一个随机数r,如果r = 0,那么index = k,否则index维持原来的的值,那么最终index就是产生的随机数的下标。